LeetCode周赛第320场记录

质量还不错的一场周赛，也可以学到不少知识。

2475. 数组中不等三元组的数目(排序+荷兰国旗问题)

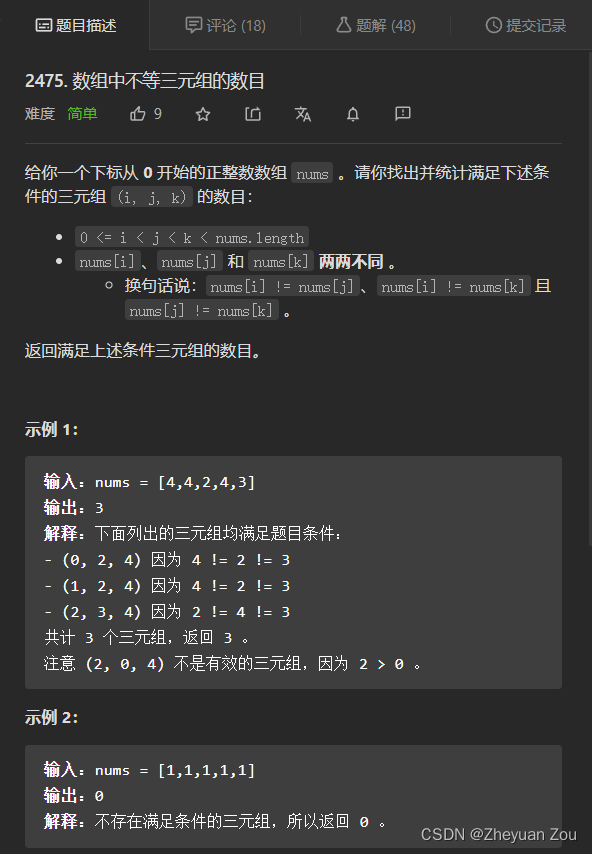
这道题非常简单，就是从头向后一一找出不含重复数字的三元组。我在比赛时直接写了一个三重循环暴力来解，这道题的数据规模是$10^2$，因此$O(n^3)$的复杂度是可以安全过的，但是暴力法不是最优解。

以下是暴力枚举的代码:

class Solution {
public:
    int unequalTriplets(vector<int>& nums) {
        int Ans = 0, n = nums.size();
		for(int i = 0 ; i < n ; ++i)
			for(int j = i + 1 ; j < n ; ++j)
				if(nums[i] != nums[j])
					for(int k = j + 1 ; k < n ; ++k)
						if(nums[k] != nums[i] && nums[k] != nums[j])
							++Ans;		
		return Ans;
    }
};

这道题还可以使用类似于荷兰国旗问题的思路来求解，因为三个数字的绝对数值不重要，所以对于每个特定数字而言，其对于答案的贡献是：

比它小的数字个数 $\times$ 自身个数 $\times$ 比它大的数字个数

可见整个区间又被分为了三个部分：

1.[0, Left)区间表示比它小的元素区间

2.[Left, i)表示当前元素的区间

3.[i, n)表示比当前元素大的区间

注意为了统一，我统统使用左闭右开区间来进行区间表示，这样写出的代码如下：

这种算法的思维难度还是不低的，时间复杂度也降低至$O(n\log n)$(排序算法复杂度)。

int unequalTriplets(vector<int>& nums) {
        int Ans = 0;
        sort(nums.begin(), nums.end());
        int n = nums.size();
        int Left = 0;
        for(int i = 1 ; i < n  ; ++i)
            if(nums[i] != nums[i - 1])
            {
                Ans += Left * (i - Left) * (n - i);
                Left = i ;
            }
        return Ans;
    }

2476. 二叉搜索树最近节点查询(中序遍历+二分)

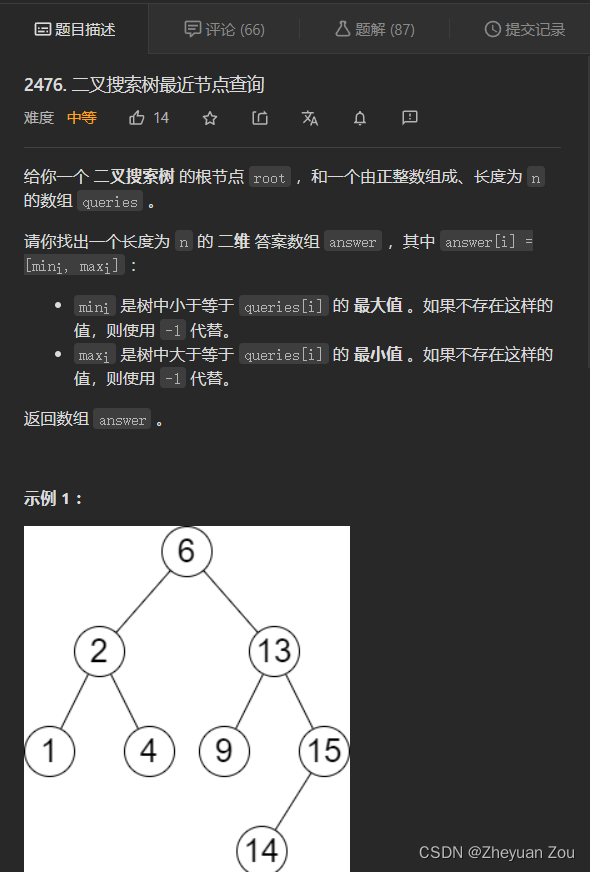
见到二叉搜索树一定要想到性质：中序遍历有序

在比赛时做这道题，我一开始还是在使用传统的递归算法来处理，写完之后发现会超时，于是更换思路到中序遍历。第二个思路就是理所当然的将二叉搜索树进行中序遍历，但是遇到二叉搜索树应该第一次就想到这种做法，因为它直接将树的问题转化为了线性序列问题。

对上述二叉搜索树进行中序遍历之后，就可以按照题意来找Min和Max了，这里可以使用二分查找来找到这个数字，C++ STL里的lower_bound和upper_bound函数可以很好地完成这个任务，但是这个地方的逻辑也比较微妙，处理不好很容易犯错，下面给出代码：

class Solution {
	vector<int> InOrder{};
	void DFS(TreeNode* root)
	{
		if(root)
		{
			DFS(root->left);
			InOrder.push_back(root->val);
			DFS(root->right);
		}
	}
public:
    vector<vector<int>> closestNodes(TreeNode* root, vector<int>& queries) {
		vector<vector<int>> Ans;
        DFS(root);                      // 得到二叉搜索树的中序遍历序列
		int n = InOrder.size();         
		for(auto Each : queries)        // O(m)
		{
			auto MinIter = upper_bound(InOrder.begin(), InOrder.end(), Each);   
			auto MaxIter = lower_bound(InOrder.begin(), InOrder.end(), Each);    
			/*
				注意这里的处理逻辑：
				Min要使用upper_bound来找
				Max要使用lower_bound来找
				同时还要判断是否是特殊的迭代器，因为这可能意味着它们没有找到解
			*/
			Ans.push_back({MinIter == InOrder.begin() ? -1 : *(MinIter - 1), MaxIter == InOrder.end() ? -1 : *MaxIter});
		}
		return Ans;

        // complexity : O(n + m * logn)
    }

2477. 到达首都的最少油耗(转化+多叉树的DFS)

这道题主要考察问题的转化，题目本身不难但是很容易会错意，我一开始想把这道题当成图的单源点最短路径问题，使用Dijkstra算法来解。但这是不对的，因为虽然每条路费一升汽油可以当作边的权重，但是这里还有一个座位seats的限制量我不知道该如何转化。

其实这就是一个简单的多叉树的DFS问题，一辆车载下尽可能多的代表就是最省油的做法，所以对于图中的(多叉树中的)每一个节点而言，将它所连接的孩子节点的代表完全聚合就是最简单的做法，多余的车可以停在父节点处不动，它们并不额外消耗汽油。

所以这个问题转化完成之后就成为了一颗多叉树的遍历问题，从任何一个节点出发，统计它的孩子节点数量到本地完成汇聚之后再通往它的父节点，一层层汇聚上去直到根节点(首都)即可。这里需要注意，树作为一种图的特殊情况，多叉树的遍历也是不需要开辟Visited数组的，因为它们不会有环的出现：

重要知识点，多叉树的遍历不需要开辟Visited的数组(因为无环)

只需要记录下父节点编号，在遍历时剔除掉即可

另外一个需要注意的点是，如何对除法做上取整，这里可以参考这篇博客。

// a,b均为整数，a除以b(上取整)的方法是：
x = (a + b - 1) / b

给出这道题的完整代码如下：

class Solution {
public:
    long long minimumFuelCost(vector<vector<int>>& roads, int seats) {
        int n = roads.size() + 1;

        // 建图
        vector<int> e[n];
        for (auto &road : roads) {
            e[road[0]].push_back(road[1]);
            e[road[1]].push_back(road[0]);
        }

        long long ans = 0;
        // DFS 统计子树大小，同时统计答案, fa是父节点编号，遍历时避开它即可
        function<int(int, int)> dfs = [&](int sn, int fa) {
            int ret = 1;
            for (int fn : e[sn]) if (fn != fa) {
                // 计算 sn -> fn 这条边的贡献
                int t = dfs(fn, sn);
                ans += (t + seats - 1) / seats;
                // 更新子树节点大小
                ret += t;
            }
            return ret;	// 返回结果到上一层
        };
        dfs(0, -1);
        return ans;
    }
};

2478. 完美分割的方案数

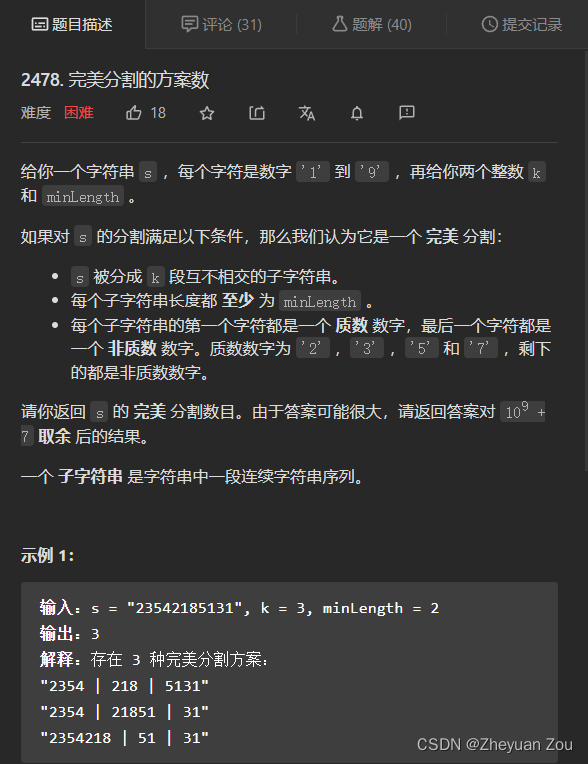
这又是一道动态规划的题目，在bilibili上看了灵茶山艾府的讲解视频，他在视频中讲解了求解动态规划问题的思考方法，这里要简单做个记录。

解决动态规划问题的思考步骤：
Q1.问题中存在哪些变量？
A1.本题中有分割子串的个数k，原字符串的长度n，每个子字符串的最小长度MinLength.

Q2.在上述的基础上复述问题，并且替换变量
A2.把一个长为j的字符串，分割出i段子字符串的合法方案数

Q3.想最后一步发生了什么？（*）
A3.最后一步我们分割出来了一个子字符串，长度为x，且它是原字符串的一个后缀

Q4.去掉最后一步，问题规模缩小了，原问题会变成什么样？
A4.把一个长度为j-x的字符串，分割成i-1段的合法方案数

Q5.得到状态转移方程
A5.从A2中可以得到，f[i][j]表示把字符串s的前j个字符分割成i段的合法方案数
(为什么是”前“j个字符，因为在A3中我们去掉的是原字符串的后缀)
从A4中可以得到，f[i][j] += f[i - 1][j']，其中j'是i-1段的结束下标，因此这里需要枚举j'
j'需要满足一些限制:
	1. j - j' + 1 >= minLength
	2. s[j']是质数，s[j]不是质数

Q6.初始值和答案分别对应于f的什么？
f[0][0] = 1;
Ans = f[k][n] 	

Q7.是否可以优化转移方程？
滚动数组 or others？
本题中j在变大的时候j'也在变大(因为要满足最短长度的限制)，所以可以有优化手段->前缀和优化

在完成上述的分析过程之后，下面直接给出本题的代码(copyright：灵茶山艾府)：
这道题可以和Weekly Contest318的最小移动总距离一起服用，尝试使用上述的流程来解决之。

class Solution {
    const int MOD = 1e9 + 7;

    bool is_prime(char c) {
        return c == '2' || c == '3' || c == '5' || c == '7';
    }

    // 判断是否可以在 j-1 和 j 之间分割（开头和末尾也算）
    bool can_partition(string &s, int j) {
        return j == 0 || j == s.length() || !is_prime(s[j - 1]) && is_prime(s[j]);
    }

public:
    int beautifulPartitions(string &s, int k, int l) {
        int n = s.length();
        if (k * l > n || !is_prime(s[0]) || is_prime(s[n - 1])) // 剪枝
            return 0;
        int f[k + 1][n + 1]; memset(f, 0, sizeof(f));
        f[0][0] = 1;
        for (int i = 1; i <= k; ++i) {
            int sum = 0;
            // 优化：枚举的起点和终点需要给前后的子串预留出足够的长度
            for (int j = i * l; j + (k - i) * l <= n; j++) {
                if (can_partition(s, j - l)) sum = (sum + f[i - 1][j - l]) % MOD; // 这里的j-l可以看成j’，双指针
                if (can_partition(s, j)) f[i][j] = sum;
            }
        }
        return f[k][n];
    }
};