题目链接：343. 整数拆分

动态规划

(1) 确定 $dp$ 数组下标含义：
$dp[i]$: 将 $i$ 拆分为至少两个正整数之后的最大乘积；
(2) 确定递推公式：
当 $i\ge 2$ 时,
设 $j$ 是 $i$ 拆分出来的第一个正整数，($1\le j\le i-1$)，有以下两种方案:
$i-j$ 不再拆分, 乘积为 $j\ast (i-j)$;
$i-j$ 继续拆分，乘积为 $j\ast dp[i-j]$;
需要遍历所有 $j$ 得到 $dp[i]$, 因此
$dp[i]=max(dp[i],max(j\ast (i-j),j\ast dp[i-j]));$
(3) $dp$ 数组初始化：
$1$ 是最小的正整数, 不能拆分, 所以 $dp[1]=0$; 其他下标均初始化为 $0$。
(4) 遍历顺序：
外循环 $i$ : $2-n$, 内循环 $j$ : $1-(n-1)$, 从小到大。
(5) 举例推导 $dp$ 数组：
$n=6$ 时:

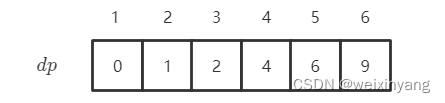
$dp[6]=9$ 即为最终结果。

代码如下：

class Solution {
public:
    int integerBreak(int n) {
        vector<int> dp(n + 1, 0);
        dp[1] = 0;
        for (int i = 2; i <= n; i++) {
            for (int j = 1; j <= i - 1; j++) {
                dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j]));
            }
        }
        return dp[n];
    }
};