一. 区间DP简单介绍

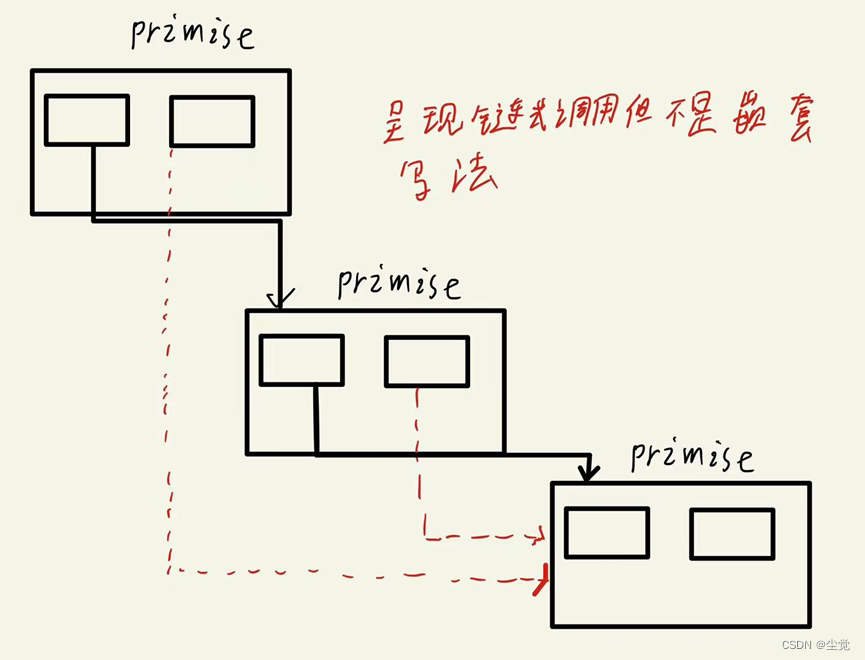
区间DP，是经常会用到的、解决区间问题的一种方法，经常以动态规划（dfs/记忆化搜索）的形式展现，最核心的思想就是枚举区间（枚举端点），寻找切割点，处理因切割点而产生的结果，进行区间累加或者选取个别区间，从而解决整体的问题。

二. 区间DP模板

枚举区间

class Solution {
    public int 区间dp(int[] v) {
        int n = v.length;
        int[][] dp = new int[n][n];
        //枚举区间长度
        for(int len = 满足题目要求的最小值; len <= n; len++){
            //枚举左端点
            for(int L = 0; L+len-1 < n; L++){
                //枚举右端点
                int R = L + len - 1;
                //设置动态规划数组的初始值
                dp[L][R] = maxvalue;
                or
                dp[L][R] = minvalue;
                //枚举区间内的可能的切割点
                for(int k = L+1; k < R; k++){
                    dp[L][R] = Math.min(dp[L][R], dp[L][k] ？ dp[k][R] ？ 因切割点而产生的特殊值);
                }
            }
        }
        //返回规定的区间范围
        return dp[0][n-1];
        or
        return dp[1][n]
        or
        others
    }
}

枚举端点

枚举端点的方法和枚举区间本质上都一样，有些题目反而用枚举端点的方法更容易思考

class Solution {
    public int 区间dp(int[] v) {
        int[][] dp = new int[v.length][v.length];
        //枚举左端点，左端点经常从大到小枚举，为什么请看下文
        for(int i = v.length-3; i >= 0; i--){
            //枚举右端点
            for(int j = i+2; j < v.length; j++){
                //dp数组初始值
                dp[i][j] = Integer.MAX_VALUE;
                or
                dp[i][j] = Integer.MIN_VALUE;
                //枚举切割点
                for(int k = i+1; k < j; k++){
                    dp[i][j] = Math.min(dp[i][j],dp[i][k]？dp[k][j]？因切割点而产生的特殊值);
                }  
            }
        }
        return dp[0][v.length-1];
    }
}

三. 区间DP经典案例

1.leetcode1312 让字符串成为回文串的最少插入次数

给你一个字符串 s ，每一次操作你都可以在字符串的任意位置插入任意字符。

请你返回让 s 成为回文串的最少操作次数。

「回文串」是正读和反读都相同的字符串。

输入：s = "mbadm"
输出：2
解释：字符串可变为 "mbdadbm" 或者 "mdbabdm" 。

输入：s = "zzazz"
输出：0
解释：字符串 "zzazz" 已经是回文串了，所以不需要做任何插入操作。

此问题和leetcode 516 最长回文子序列属于同类题目[Ref. 3]：

" 求的是将 s 变成回文串需要添加的最少字符数，所以我们只用求最长回文子序列长度即可，然后字符串 s 中除去最长回文子序列，剩下的字符就是不构成回文子序列的字符，添加与其同等数量的字符，将 s 构成回文串。"

**leetcode 516 最长回文子序列

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

输入：s = "bbbab"
输出：4
解释：一个可能的最长回文子序列为 "bbbb" 。

输入：s = "cbbd"
输出：2
解释：一个可能的最长回文子序列为 "bb" 。

class Solution {
    public int longestPalindromeSubseq(String s) {
        int len = s.length();
        int[][] dp = new int[len][len];
        for(int i = len-1; i >= 0; i--){
            dp[i][i] = 1;
            for(int j = i+1; j < len; j++){
                if(s.charAt(i) == s.charAt(j)){
                    dp[i][j] = dp[i+1][j-1] + 2;
                }
                else{
                    dp[i][j] = Math.max(dp[i+1][j],dp[i][j-1]);
                }
            }
        }
        return dp[0][len-1];
    }
}

此题详解：

子串和子序列问题-动态规划向_子串子序列_ForwardSummer的博客-CSDN博客

再看此题

class Solution {
    public int minInsertions(String s) {
        int len = s.length();
        int[][] dp = new int[len+1][len+1];
        for(int i = len-1; i>= 0; i--){
            dp[i][i] = 1;
            for(int j = i+1; j < len; j++){
                if(s.charAt(i) == s.charAt(j)){
                    dp[i][j] = dp[i+1][j-1] + 2;
                }
                else{
                    dp[i][j] = Math.max(dp[i+1][j],dp[i][j-1]);
                }
            }
        }
        return len-dp[0][len-1];
    }
}

本题小结：

（1）dp[i][j] 代表从i到j的区间(左闭右闭)内最长的回文子序列的长度

（2）那么，当s.charAt(i) == s.charAt(j)， $dp[i][j] = dp[i+1][j-1] + 2$

（3）当s.charAt(i) != s.charAt(j)， $dp[i][j] = Math.max(dp[i+1][j],dp[i][j-1])$

（4）字符串 s 中除去最长回文子序列，剩下的字符就是不构成回文子序列的字符

2.leetcode1039 多边形三角剖分的最低得分

你有一个凸的 n 边形，其每个顶点都有一个整数值。给定一个整数数组 values ，其中 values[i] 是第 i 个顶点的值（即顺时针顺序）。

假设将多边形剖分为 n - 2 个三角形。对于每个三角形，该三角形的值是顶点标记的乘积，三角剖分的分数是进行三角剖分后所有 n - 2 个三角形的值之和。

返回多边形进行三角剖分后可以得到的最低分。

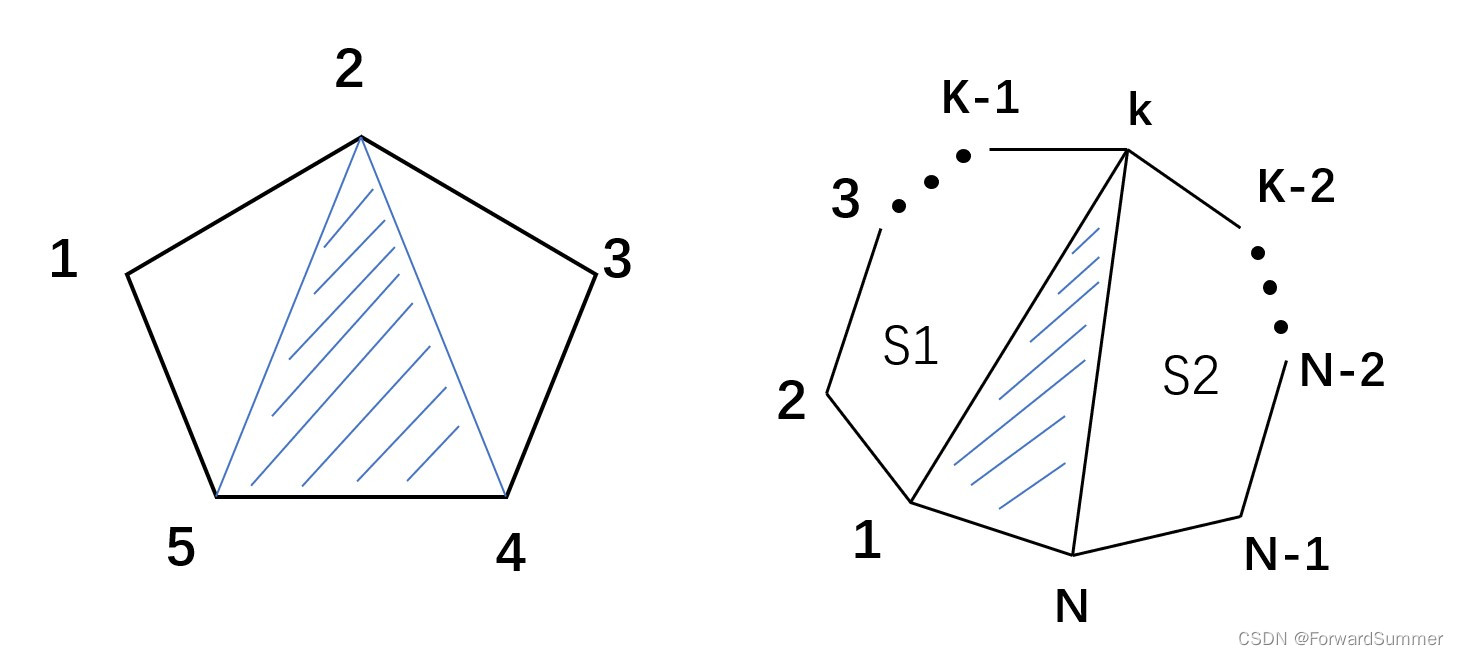
1.边长为n的多边形形产生的三角形为n-2个,n>=3

2.当边为5时，固定一个边当作底（比如4-5），选择一个顶点（比如2），
  蓝色线表示的三角形将整个五边形分为三个部分。

3.当边长为5时，知道当前三角形面积（蓝色部分），知道左右的三角形面积，
  即可得到所有的三角形面积，进而求其和。

4.当来到多边形，依然找到一个三角形（求出其面积），将三角形左右两边求出（S1+S2），
  即可求所有的三角形构成的面积之和。

5.求出所有的可能性，选择其中一个最小的。

枚举左右端点 DFS


class Solution {
    int[] v;
    public int minScoreTriangulation(int[] v) {
        this.v = v;
        return dfs(0,v.length-1);
    }
    public int dfs(int i, int j){
        if(i+1 == j) return 0;
        int res = Integer.MAX_VALUE;
        for(int k = i+1; k < j; k++){
            res = Math.min(res,dfs(i,k)+dfs(k,j)+v[i]*v[j]*v[k]);
        }
        return res;
    }
}

本方法小结：

（1）dfs的意义代表从i端点到j端点构成的多边形的最小面积，相当于上图的{1~N+N~1}（顺时针）

（2）以i和j为底，k为顶点的三角形会把整个多边形分成更小的子问题

（3）左边的子问题为dfs(i,k)，右边的子问题为dfs(k,j)，已经解决的问题为当前这个三角形，即为v[i]*v[j]*v[k]

（4）当i+1 == j时，只有两个点，构不成三角形，返回0

DFS超时，因为算法复杂度是 $O(n^3)$ ，数据很容易超时，接下来改成记忆化搜索。

记忆化搜索

class Solution {
    int[][] memo;
    int[] v;
    public int minScoreTriangulation(int[] v) {
        this.v = v;
        memo = new int[v.length][v.length];
        for(int[] i : memo){
            Arrays.fill(i,-1);
        }
        return dfs(0,v.length-1);
    }
    public int dfs(int i, int j){
        if(i+1 == j) return 0;
        if(memo[i][j] != -1) return memo[i][j];
        int res = Integer.MAX_VALUE;
        for(int k = i+1; k < j; k++){
            res = Math.min(res,dfs(i,k)+dfs(k,j)+v[i]*v[j]*v[k]);
        }
        memo[i][j] = res;
        return res;
    }
}

动态规划

class Solution {
    public int minScoreTriangulation(int[] v) {
        int[][] dp = new int[v.length][v.length];
        for(int i = v.length-3; i >= 0; i--){
            for(int j = i+2; j < v.length; j++){
                dp[i][j] = Integer.MAX_VALUE;
                for(int k = i+1; k < j; k++){
                    dp[i][j] = Math.min(dp[i][j],dp[i][k]+dp[k][j]+v[i]*v[j]*v[k]);
                }  
            }
        }
        return dp[0][v.length-1];
    }
}

本方法小结：

（1）dp[i][j]代表从i到j区间内所构成的三角形面积的最小值

（2）i从length-3开始可以理解成从i开始最少需要三条边构成三角形，j和k都比i要大，所以从i-3开始满足能成立一个三角形，j从i+2开始是因为中间需要留至少一个k的空间，最后k在i和j中取值，左虚右虚

（3）由于k比i大，而 dp[i][j]需要dp[i][k]作为基础，所以i的转移方向为从大到小，同理，j的方向为从小到大

经典枚举区间

class Solution {
    public int minScoreTriangulation(int[] v) {
        int n = v.length;
        int[][] dp = new int[n][n];
        for(int len = 3; len <= n; len++){
            for(int L = 0; L+len-1 < n; L++){
                int R = L + len - 1;
                dp[L][R] = 0x3f3f3f3f;
                for(int k = L+1; k < R; k++){
                    dp[L][R] = Math.min(dp[L][R], dp[L][k] + dp[k][R] + v[L]*v[R]*v[k]);
                }
            }
        }
        return dp[0][n-1];
    }
}

本方法小结：

（1）以上的方法都是枚举左右端点，此方法为经典的枚举区间

（2）区间长度len最少从3开始，长度大于等于3才能构成三角形，枚举左端点，右端点为左端点加上区间长度，然后枚举中间的k点（相当于三角形的顶点）

（3）一般的区间DP都是枚举区间，然后枚举左右端点，这题可以直接枚举左右端点，然后枚举中间的k点