1.还原AhutOj
如图,位置1和2的最大值是3,位置1可以直接放3,同理,位置5可以直接放5
位置1和位置2的最大值是3,位置2和位置3的最大值是4,位置3和位置4的最大值是4,所以位置2只能取3和4的最小值,同理,位置3只能取4和4的最小值,位置4只能取4和5的最小值
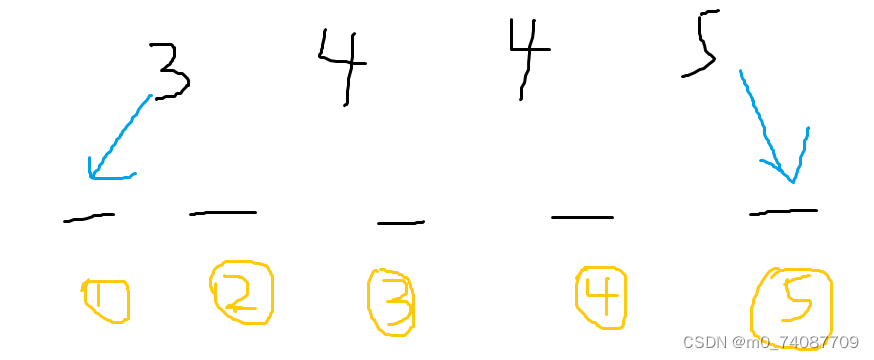



AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 2e5 + 10;
int a[N];
int b[N];
int main()
{
int t;
cin >> t;
while (t--) {
int n;
cin >> n;
for (int i = 1; i <= n-1; i++) cin >> a[i];
for (int i = 1; i <= n; i++) {
if (i == 1) {
b[i] = a[i];
}
else if (i < n) {
b[i] = min(a[i - 1], a[i]);
}
if (i == n) b[i] = a[i - 1];
}
for (int i = 1; i <= n; i++) cout << b[i] << " ";
cout << endl;
}
return 0;
}2.三进制异或AhutOj
观察样例,可以发现第一个字符肯定是2,分成1和1
后面的字符如果是0的话就分成0和0,如果是2的话就分成1和1(平分的话可以使得a,b两者之间的最大值最小),但如果是1的话就没办法平分了,就只能分成1和0,这样就势必会一个大一个小,以这为分界点,之后分的时候就不要平分了,分到1的肯定比分到0的要大,所以现在要做的就是使得那个肯定大的数就可能小
之后分的时候:如果是字符0,分成0和0
如果是1,肯定大的那个数分0,肯定小的的那个数分1
如果是2,肯定大的那个数分0,肯定小的的那个数分2


AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 100010;
int a[N];
int b[N];
bool flag;
int main()
{
int t;
cin >> t;
while (t--) {
flag = false;
int n;
cin >> n;
string s;
cin >> s;
int len = s.size();
a[0] = 1;
b[0] = 1;
for (int i = 1; i <len; i++) {
if (!flag) {
if (s[i] == '0') {
a[i] = 0;
b[i] = 0;
}
else if (s[i] == '1') {
a[i] = 1;
b[i] = 0;
flag = true;
}
else if (s[i] == '2') {
a[i] = 1;
b[i] = 1;
}
}
else {
if (s[i] == '0') {
a[i] = b[i] = 0;
}
else if (s[i] == '1') {
a[i] = 0;
b[i] = 1;
}
else if (s[i] == '2') {
a[i] = 0;
b[i] = 2;
}
}
}
for (int i = 0; i <len; i++) cout << a[i];
cout << endl;
for (int i = 0; i <len; i++) cout << b[i];
cout << endl;
}
return 0;
}3.Good子串AhutOj
用前缀和,字符为0的时候加-1,字符为1的时候加1,和为0的时候说明0和1的个数相同
做法是记录某前缀和第一次(只记录第一次的)出现时的下标,然后当该前缀和的值再次出现时,两下标所夹的子串的和就是0,该子串就是好子串
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1000010;
int a[N];
int sum;
int id[N];
int maxn = 1e5 + 10;
int main()
{
int n;
cin >> n;
string s;
cin >> s;
for (int i = 0; i < n; i++) {
if (s[i] == '0') a[i+1] = -1;
else a[i+1] = 1;
}
int ans = 0;
for (int i = 1; i <= n; i++) {
sum += a[i];
if (sum == 0) ans = i;//第一次找到好子串,记录子串长度,不能省去,因为省去的话,如果到最后一个前缀和才为0的话或者后面没有前缀和为0的,就无法把该子串记下来了
else if (id[sum+maxn]) ans = max(ans, i - id[sum+maxn]);//找到了好子串,i-id[sum+maxn]即好子串的长度
else id[sum+maxn] = i;//记录每一个前缀和第一次出现的下标,加上一个偏移量maxn保证下标为正,不会为负从而导致溢出
}
cout << ans << endl;
return 0;
}4.二分图但是不匹配AhutOj



AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long LL;
const int N = 100010, M = 200010;
int n, m;
int h[N], e[M], ne[M], idx;
int color[N];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool dfs(int u, int c) {
color[u] = c;
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
if (!color[j]) {
if (!dfs(j, 3 - c)) return false;
}
else if (color[j] == c) return false;
}
return true;
}
LL cnt1;
LL cnt2;
int main()
{
cin >> n ;
memset(h, -1, sizeof h);
int m = n - 1;
while (m--) {
int u, v;
cin >> u >> v;
add(u, v), add(v, u);
}
bool flag = true;
for (int i = 1; i <= n; i++) {
if (!color[i]) {
if (!dfs(i, 1)) {
flag = false;
break;
}
}
}
if (!flag) {
cout << 0 << endl;
return 0;
}
for (int i = 1; i <= n; i++) {
if (color[i] == 1) cnt1++;
else if (color[i] == 2) cnt2++;
}
cout << cnt1 * cnt2 - (n - 1) << endl;
return 0;
}5.https://atcoder.jp/contests/abc299/tasks/abc299_d
(atcoder里的题)


因为最左边是0,最右边是1,所以一定存在01,不一定存在10,要想找到一个位置p使得sp!=sp+1,只需要找到01的0位置就行
一直二分,长度为2的时候找到的就是01,l就是0的位置,r就是1的位置
用二分,在l到r-1二分(不需要l==r时才结束,只要l==r-1时就可以结束了,只要找到0的位置就行了)
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
int main() {
int n;
cin >> n;
int l = 1, r = n;
while (l < r-1) {
int mid = (l + r) / 2;
cout << "? " << mid << endl;
char ch;
cin >> ch;
if (ch== '0') l = mid;
else if (ch == '1') r = mid;
}
cout << "! " << l << endl;
return 0;
}