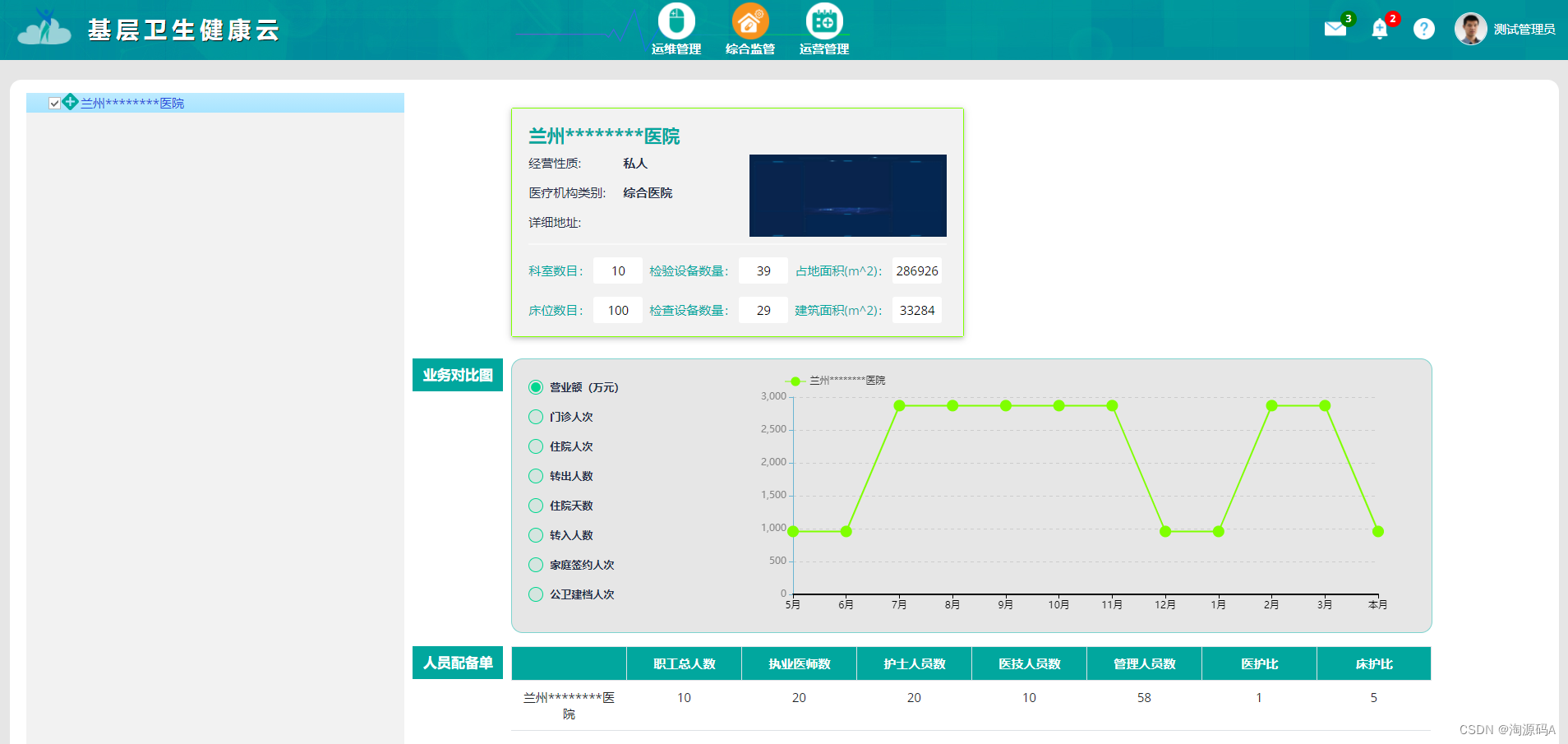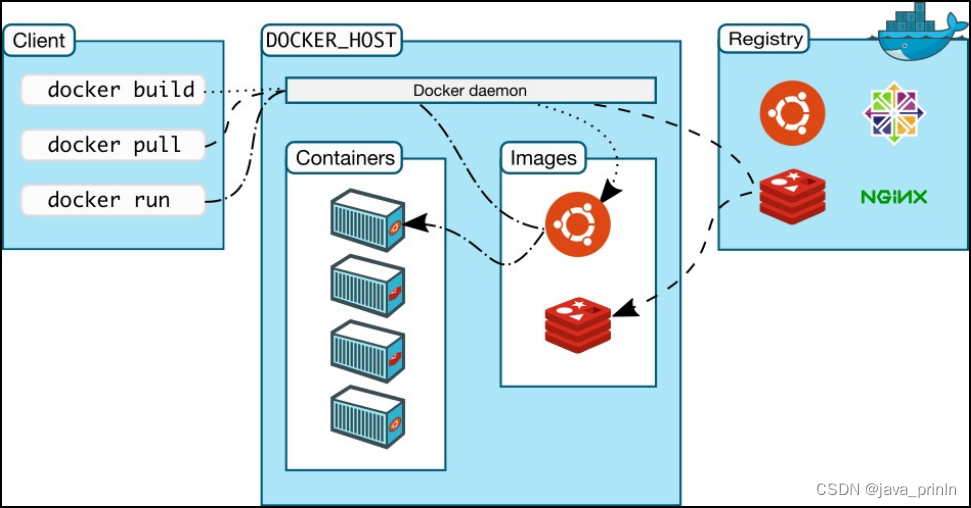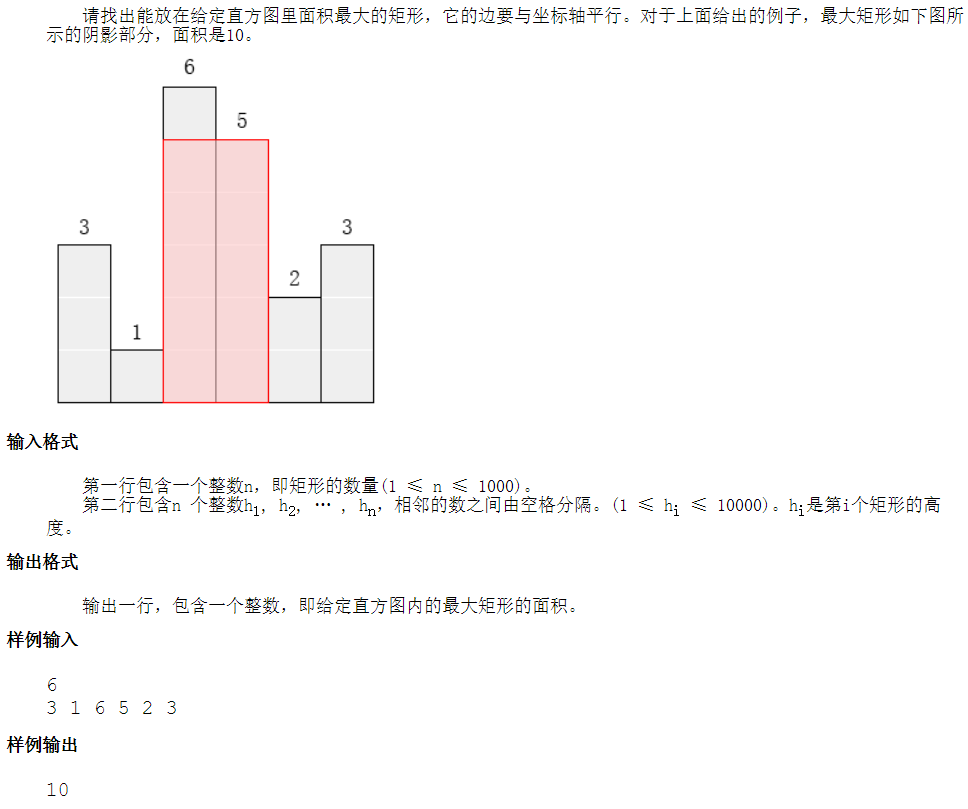
首先我们可以先根据数据范围反推时间复杂度，比如，数据范围n <= 1000,我们可以将时间复杂度控制在O(n²), O(n²)logn

思路上比较容易想到的是枚举所有情况，然后输出面积最大的情况即可

可以在第一重循环枚举i，表示从第i个矩形开始往后，然后第二重循环枚举j，表示从第i个矩形往后到第j个矩形所组成的面积，此时我们已经确定了组成的矩形的底是多大即j-i+1(如果下标从1开始)，那么我们再确定高即可，根据题意不难得知，高是由我们选取的矩形区间[ i , j ]之间的矩形的最小高决定的，比如我们选取了第2个矩形到第5个矩形，那么高就是由最小矩形第2个矩形决定的，因此我们再设置第三重循环枚举得到矩形区间[ i , j ]的最小高

但是一开始我们就确定的大致的时间复杂度要求，如果按照上面的思路已经达到三重循环是肯定不能满足的，因此我们需要优化

这里我们想到尝试空间换时间，即使用一个数组来存储矩形区间的最小高

int book[1010][1010];//辅助数组定义为存储矩形[i,j]的最小高 

于此同时我们并不需要提前将数组的值设置好，只需在遍历矩形区间时更新数组即可

 如上图所示，矩形 i 到 j 的最小高在遇到一个新加入的矩形时要么被刷新最小值要么不变

这样我们就避免了三重循环，而缩小到了二重循环

#include<iostream>
#include<iomanip>
#include<cstring>
using namespace std;

int n,maxn=INT_MIN;
int arr[1010];
int book[1010][1010];//辅助数组定义为存储矩形[i,j]的最小高 

int main(){
	cin>>n;
	memset(book,0x3f,sizeof(book));//初始化为最大值，否则在遍历时会出现0的情况 
	for(int i=1;i<=n;i++){
		cin>>arr[i];
		book[i][i]=arr[i];//初始化 
	}	
	for(int i=1;i<=n;i++){
		for(int j=i;j<=n;j++){
			book[i][j]=min(book[i][j-1],arr[j]);//一边遍历一边更新区间最小高数组		
			int area=(j-i+1)*book[i][j];//高由区间最小高决定 
			if(area>maxn){//取最大面积 
				maxn=area;
			}
		}
	}
	cout<<maxn<<endl;
	return 0;
}

需要注意的是辅助数组的初始化问题，因为需要取最小值，所以我们将其所有元素初始化为最大值

思路2（参考CCF最大的矩形）：

实际上我们可以确定的是我们最终选定的矩形的高必然是所给高中的其中一个，而我们最终的矩形的高是由其中的最小高决定的，因此我们为了维持我们所选取的高，那么它能向左右扩展的距离就是底了，扩展的条件就是左右矩形的高比我们选取的矩形的高要大于等于

具体代码参考这里