作者:王再军
不管是什么样的数据,投其所好,才能够优化代码性能。本文将用一个实际用例为大家分享如何通过用心组织的代码来提升性能。
一、出现性能差别的代码
CPU友好的代码与我们平时的那些CRUD操作可能没什么关系。但是用心组织的代码其实也能让性能提升百倍。我们不应该停留在CRUD的漩涡中。今天我给大家带来一个很神奇的现象,文章不长,原理通用,还请大家耐心看完。
我们可以先看下面的矩阵计算。大家也可以自己思考一下,如果是你来实现一个矩阵的乘法,你会怎么来做。
下图是我给出的A、B、C 三个解题的思路。大家觉得在JVM里面,下面的代码性能会有区别么?如果有的话,哪一个会快一点?如果没有的话,又为什么?

下图是benchmark运行的结果(具体的运行代码和结果查看文末附件),是否和你想的一样呢。

x轴是计算数组的大小,y轴是所消耗的时间。
最上两条线是B代码块的结果,中间是A代码块的结果,最下面是C代码块的结果。
从运行时间角度看结果是:TC < TA < TB。从性能角度看结果是:PC > PA > PB。
大家猜对结果了么,是不是很你想的一样呢?如果不是的话,那就慢慢往下面看。
二、为什么会有性能差别?
要想知道这个问题的答案,我们需要知道两个知识点。
-
首先,我们需要知道Java二维数组的存储结构是什么样子的。
-
其次,我们需要知道CPU在计算的时候它L1、L2、L3的缓存机制。
2.1 知识点
2.1.1 知识点一:Java二维数组的存储结构
下图便是Java二维数组的一个存储方式示意图,意思是 int[][] array_A = new int[4][3]。

在一个数组里面存的都是“指针”,指向真实存放数据的地址块。
每一行的数据是连续的地址,但是行与行之间的地址就不一定连续了。这一点很重要,后面会用到。
2.1.2 知识点二:CPU的缓存机制
CPU架构是会演进的,高低端的参数也不一定相同。但我们毕竟不是CPU的制造者,不必每一个CPU都去细扣,我们只需要理解他的原理,在适当的时候做一些抽象方便理解就可以。
下图是我当前Mac的CPU参数,大家需要注意2个东西,L2缓存、L3缓存。这2个参数就是影响我们今天讨论的性能的主要因素。

下面是各个缓存的CPU的访问时间:
L1 、L2、L3、主存的大小是逐渐增大,速度是逐渐减小的。

下面是现代CPU的一个架构示意图:

其中:
-
Regs,是寄存器。
-
d-cache,是数据缓存。
-
i-cache,是指令缓存。本次我们并不讨论这个缓存快的影响。
CPU的缓存里面还有很多的细节,知道上面的信息就已经足够我们理解今天的问题了。
2.2 性能损失的原因 — 缓存命中率
有了上面的各级别的缓存参考之后,我们可以想象一下,如果把上面的图像换成是我们的二维数组呢。是不是就是下面这样(可能没有那么严谨,但是不妨碍我们理解)。
在RAM(主存)的数据是这样的:

L3缓存就是这样的(红色框选中部分):
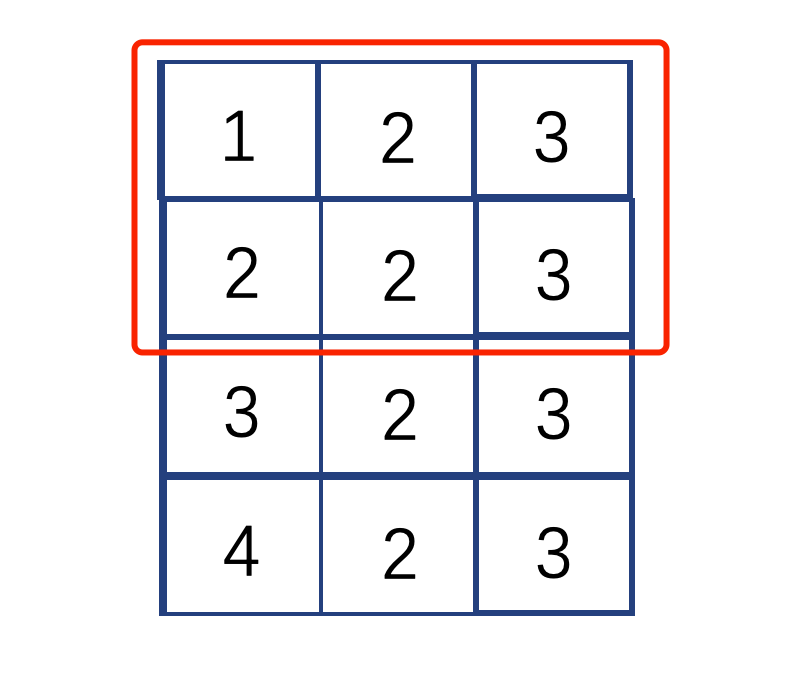
L2缓存就是这样的(红色框选中部分):
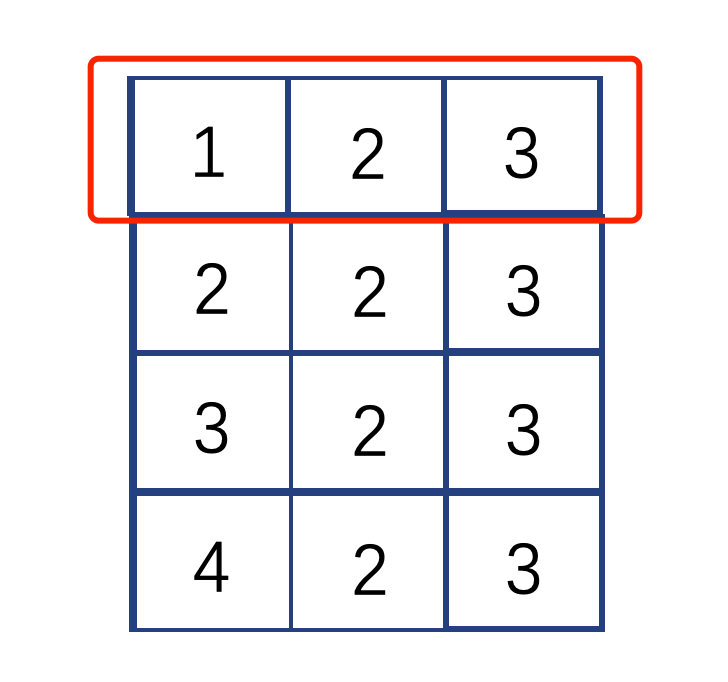
有了这个这些层级的缓存之后,CPU在计算的时候就可以不用来回的到速度极慢的RAM(主存)中去找数组的数据了。
2.2.1 友好的遍历方式
假设上面的数据的变量名称是A,成员使用a来表述。
我们取数据按照从左到右,再从上到下的顺序来进行遍历。
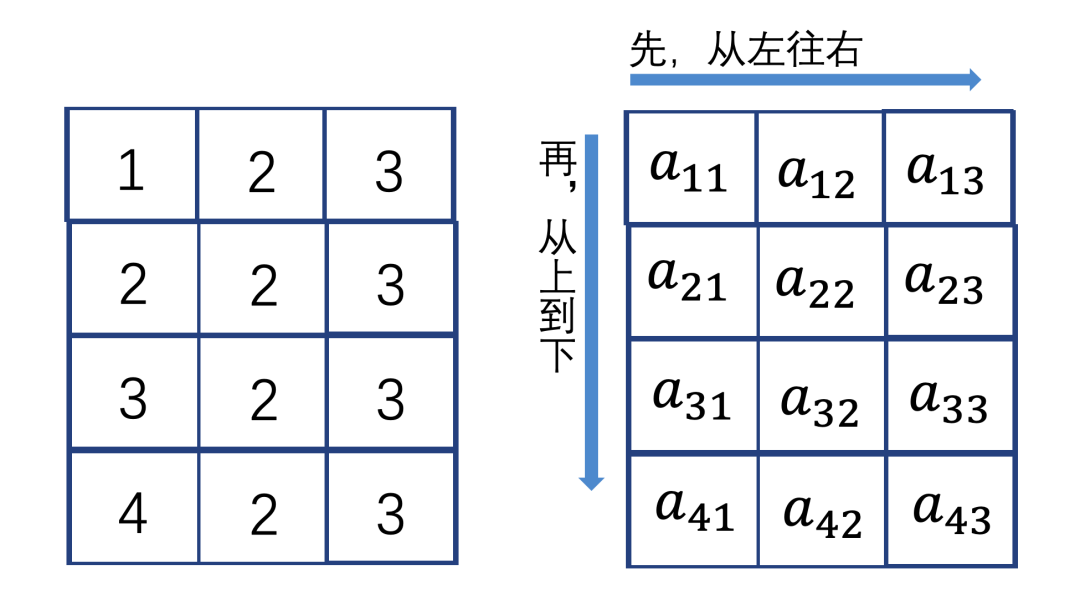
对于L2缓存来说:
第一次获取数据a11(“1”)的时候其实是没有数据的,所以会耗时去把a11,a12,a13(“1,2,3”)都取回来缓存起来。
当第二次取a12、a13的时候候就直接从L2缓存取了。这样cache命中率就是 66.7%。
对于L3的情况类似。这样的遍历方式对于CPU来说是一个很友好且高效的。
-
C代码块就是这种横向优先的访问方式。
-
A代码块里面对arrays_A的方式是横向优先遍历的,但是在处理arrays_B的时候就是纵向遍历的(也就是下面即将提到的方式)。
-
B代码块所有的访问都是纵向的(不友好的遍历方式)。因为发挥不出CPU缓存的效果,所以性能最差。
2.2.2 不友好的遍历方式
从上到下,再从左到右。
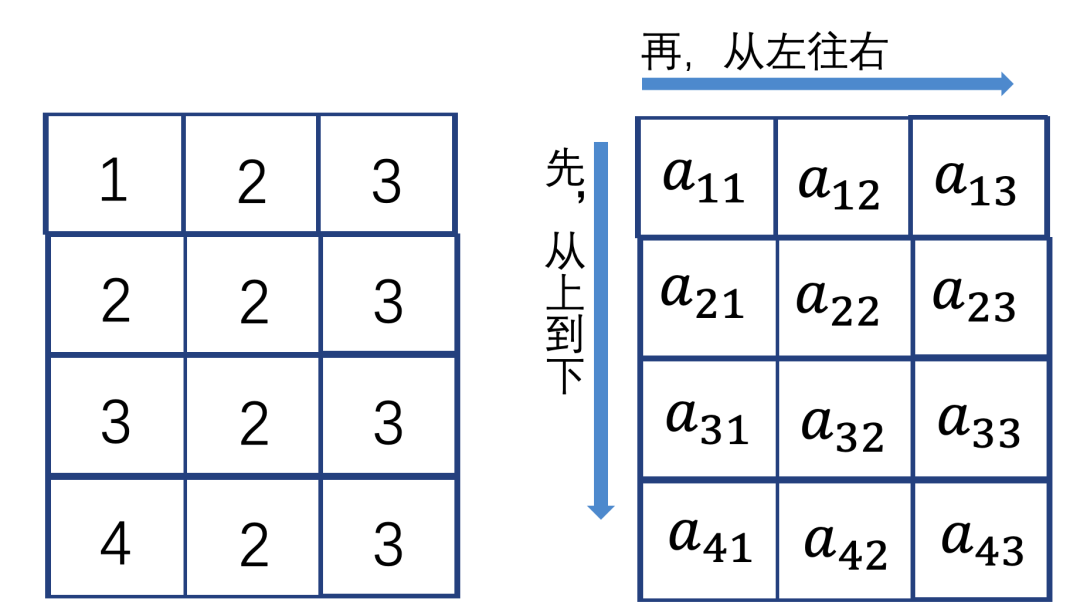
为什么这是一个不好的遍历方式呢?
这个得结合上一节Java的二维数组的存储结构一起看。再来回顾一下:

从上面的存储的结构图来看,其实a11,a12,a13 与 a21,a22,a23行与行之间并不是连续的。所以对于L1、L2、L3缓存来说很有可能是不能一起被缓存的(这里用了可能,具体得看L1、L2、L3的容量和数组的大小)。虽然是可能,但是通常都不会一起出现。
有了这个知识之后,我们再来看,先从上到下,再从左到右的顺序的缓存命中率。
-
第一次,获取a11,但是缓存里面没有,找到a11之后就把a11,a12,a13缓存下来了。
-
第二次,获取a21,但是缓存里面没有,找到a21之后就把a21,a22,a23缓存下来了,假设有CPU有两行的缓存空间。
-
第三次,获取a31,但是缓存里面没有,找到a31之后把a31,a32,a33缓存下来,并且把a11,a12,a13替换掉(缓存的空间有限,虽然具体的替换策略有很多种,并且还和数据本身的Hash有关系,这里就假设把第一次的结果覆盖了)。
-
后面的逻辑重复之前的步骤。最后得到的缓存命中率就是0%。
结合文章开头的缓存速率表格,我们就不难发现,如果我们每次都不命中缓存的话,那么延迟带来的耗时将会相差一个数量级。
三、总结
再来回顾一下我们之前的问题。

-
C代码块是横向优先的访问方式。
-
A代码块里面对arrays_A的方式是横向顺序访问的,但是在处理arrays_B的时候就是纵向遍历的。
-
B代码块所有的访问都是纵向的(不友好的遍历方式)。因为发挥不出CPU缓存的效果,所以性能最差。
Java的二维数组在内存里面是行连续的,但是行与行之间不一定连续。CPU在缓存大小有限的情况下,不可能把所有的数据都缓存下来。再加上每一层级访问速度的硬件限制,就导致了上面的性能结果。
相信大家也和我一样,知道原理之后,也不是那么迷惑了。
在实际的业务环境中,我们不一定能遇到这种纯计算的场景。但是我们还是应该尽量顺序访问数据,不管是什么样的数据。投其所好,才能够优化代码性能。
其次,我们在访问数据的时候,还是需要了解各种语言背后实际的存储结构和CPU的缓存原理,本次是讲述的是Java,但是这个思想其他语言其实也是受用的。
四、附件
4.1 运行的环境
系统参数:
JMH version: 1.36
VM version: JDK 11.0.13, Java HotSpot(TM) 64-Bit Server VM, 11.0.13+10-LTS-370
型号名称:MacBook Pro
型号标识符:MacBookPro15,2
处理器名称:四核Intel Core i5
处理器速度:2.4 GHz
处理器数目:1
核总数:4
L2缓存(每个核):256 KB
L3缓存:6 MB
超线程技术:已启用
内存:16 GB
系统固件版本:1715.60.5.0.0 (iBridge: 19.16.10647.0.0,0)4.2 整个benchmark的java代码
ArrayTestBenchmark
import org.openjdk.jmh.annotations.*;
/**
* 矩阵 C = AB 的计算
*
* @author wzj
* @date 2023/02/09
*/
@BenchmarkMode(Mode.AverageTime)
@State(value = Scope.Benchmark)
// 预热3次
@Warmup(iterations = 3, time = 1)
// 循环 10 次
@Measurement(iterations = 10, time = 1)
public class ArrayTestBenchmark {
private final int N = 1000;
private final int[][] arrays_A = new int[N][N];
private final int[][] arrays_B = new int[N][N];
@Setup
public void setUp() {
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
arrays_A[i][j] = i + j;
arrays_B[i][j] = i + j;
}
}
}
@Benchmark
public void ijk() {
final int[][] arrays_C = new int[N][N];
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
int sum = 0;
for (int k = 0; k < N; k++) {
sum += arrays_A[i][k] * arrays_B[k][j];
}
arrays_C[i][j] += sum;
}
}
assert arrays_C.length > 0;
}
@Benchmark
public void jik() {
final int[][] arrays_C = new int[N][N];
for (int j = 0; j < N; j++) {
for (int i = 0; i < N; i++) {
int sum = 0;
for (int k = 0; k < N; k++) {
sum += arrays_A[i][k] * arrays_B[k][j];
}
arrays_C[i][j] += sum;
}
}
assert arrays_C.length > 0;
}
@Benchmark
public void jki() {
final int[][] arrays_C = new int[N][N];
for (int j = 0; j < N; j++) {
for (int k = 0; k < N; k++) {
int r_B = arrays_B[k][j];
for (int i = 0; i < N; i++) {
arrays_C[i][j] += arrays_A[i][k] * r_B;
}
}
}
assert arrays_C.length > 0;
}
@Benchmark
public void kji() {
final int[][] arrays_C = new int[N][N];
for (int k = 0; k < N; k++) {
for (int j = 0; j < N; j++) {
int r_B = arrays_B[k][j];
for (int i = 0; i < N; i++) {
arrays_C[i][j] += arrays_A[i][k] * r_B;
}
}
}
assert arrays_C.length > 0;
}
@Benchmark
public void kij() {
final int[][] arrays_C = new int[N][N];
for (int k = 0; k < N; k++) {
for (int i = 0; i < N; i++) {
int r_A = arrays_A[k][i];
for (int j = 0; j < N; j++) {
arrays_C[i][j] += r_A * arrays_B[k][j];
}
}
}
assert arrays_C.length > 0;
}
@Benchmark
public void ikj() {
final int[][] arrays_C = new int[N][N];
for (int i = 0; i < N; i++) {
for (int k = 0; k < N; k++) {
int r_A = arrays_A[k][i];
for (int j = 0; j < N; j++) {
arrays_C[i][j] += r_A * arrays_B[k][j];
}
}
}
assert arrays_C.length > 0;
}
}4.3 多次运行benchmark的结果
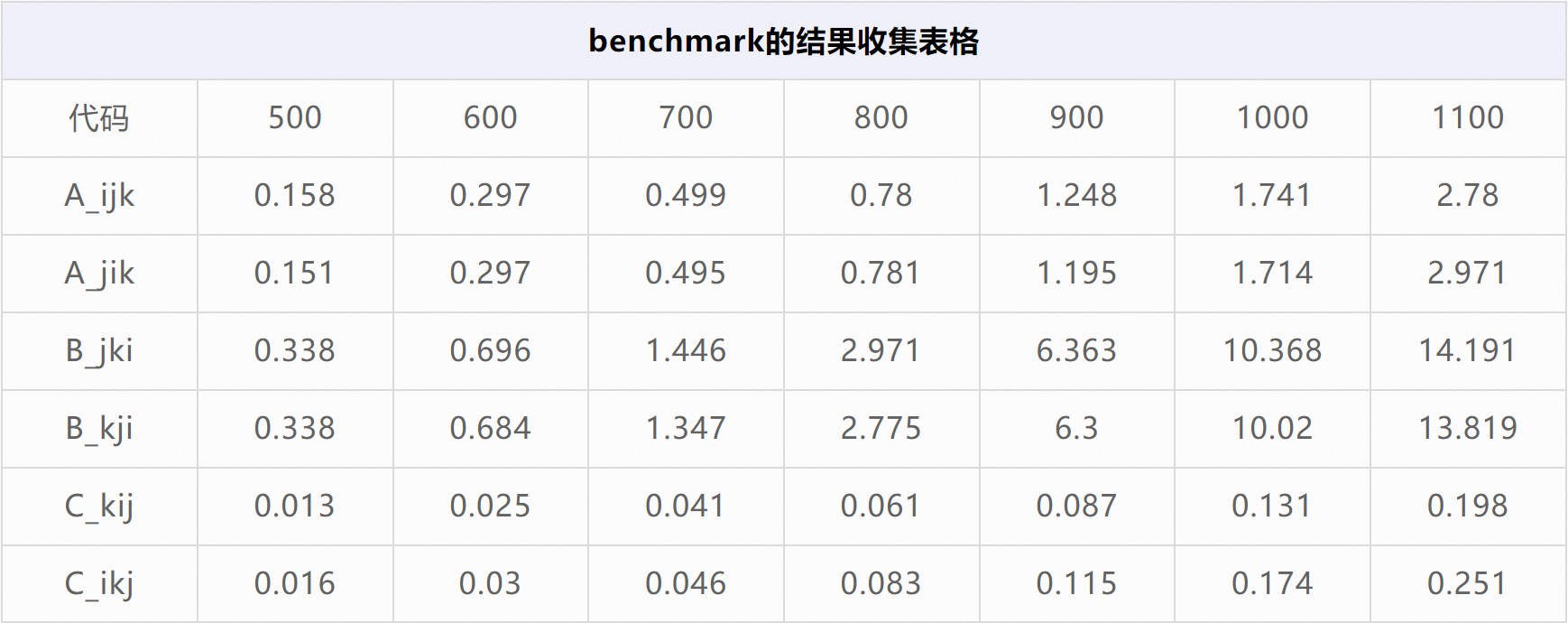
引用
[01] 《深入理解计算机操作系统》
[02] 《深入理解Java虚拟机》