周期信号的傅里叶变换计算
- 一、周期信号的傅里叶变换存在的条件
- 二、周期信号的傅里叶变换
- 例题:
一、周期信号的傅里叶变换存在的条件
典型非周期信号(如指数信号,矩形信号等)都是满足绝对可积(或绝对可和)条件的能量信号,其傅里叶变换存在。但绝对可积(或绝对可和)条件仅是充分条件,而不是必要条件。在引入广义函数的概念,允许傅里叶变换采用冲激函数的前提下,
使许多原本并不满足绝对可积条件的功率信号(周期和非周期的)以及某些非功率、非能量信号都可以获得傅里叶变换。这样就可以把周期信号和非周期信号的分析方法统一起来,也可把周期信号的傅里叶级数与傅里叶变换统一起来,使傅里叶变换得到
更广泛的应用。
由于在这一类并不满足绝对可积条件周期信号的傅里叶变换中,一般都存在冲激函数,所以把它们称为含有冲激函数的傅里叶变换。例如:
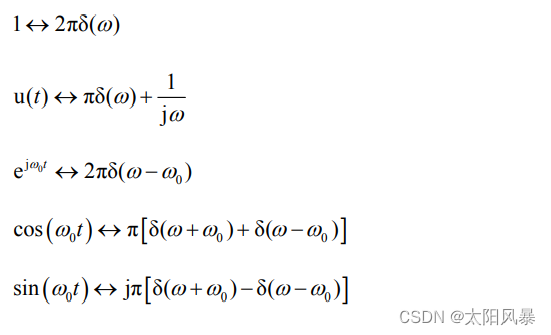
二、周期信号的傅里叶变换
对于周期信号的傅里叶级数表达式,令周期信号的周期趋于无穷大,这样,周期信号就变成非周期信号,于是傅里叶级数演变成傅里叶变换,周期信号的离散频谱过渡成连续频谱。傅里叶级数用于周期信号的频谱分析,而傅里叶变换则用于非周期信号的频谱分析。现在,我们利用冲激函数的概念,从而可以将傅里叶级数看做傅里叶变换的特殊情况。
推论:

上式表明,周期信号的傅里叶变换或频谱密度函数是由(无穷多个)冲激函数所组成,位于谐波频率 nω0 处冲激函数的强度是第 n 个傅里叶级数系数 Fn 的 2π 倍。
例题:
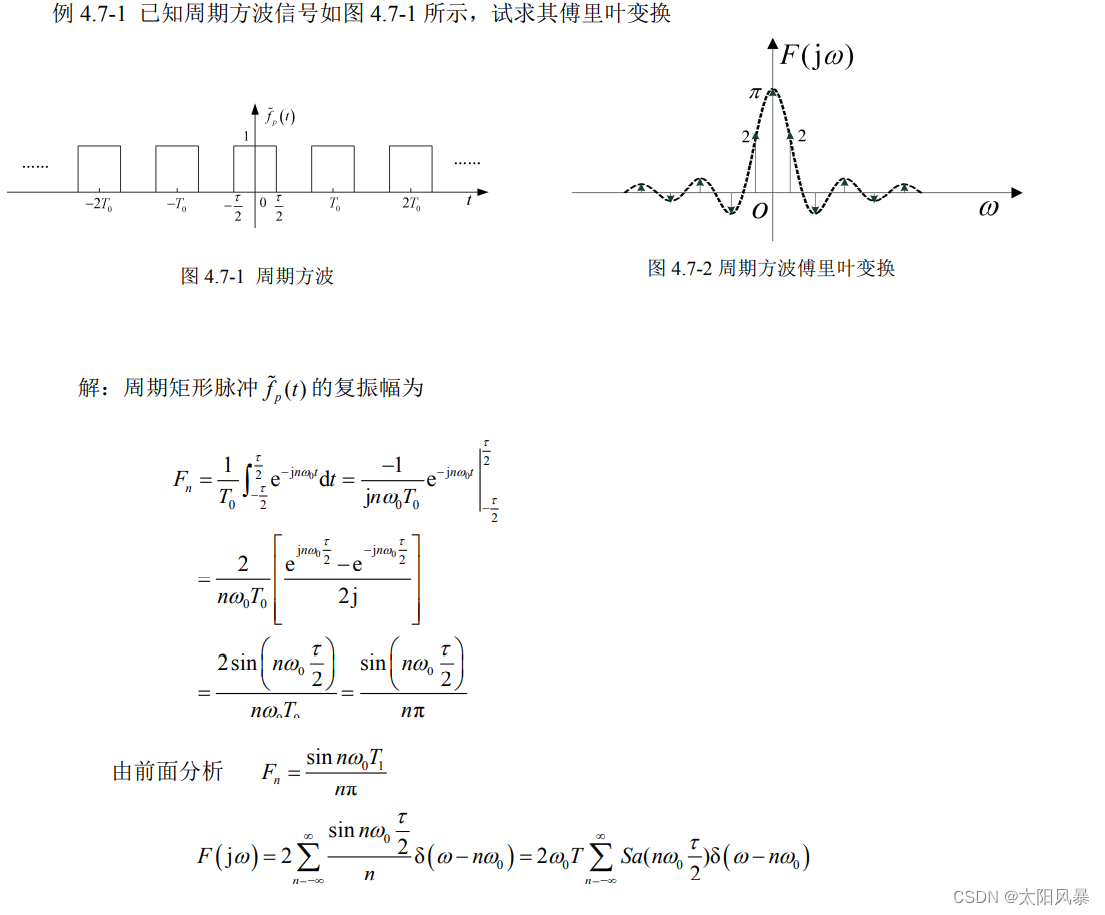


![[附源码]SSM计算机毕业设计新冠疫苗线上预约系统JAVA](https://img-blog.csdnimg.cn/19572828ebfd4181923e74dc9a38652c.png)