https://codeforces.com/contest/4/problem/D
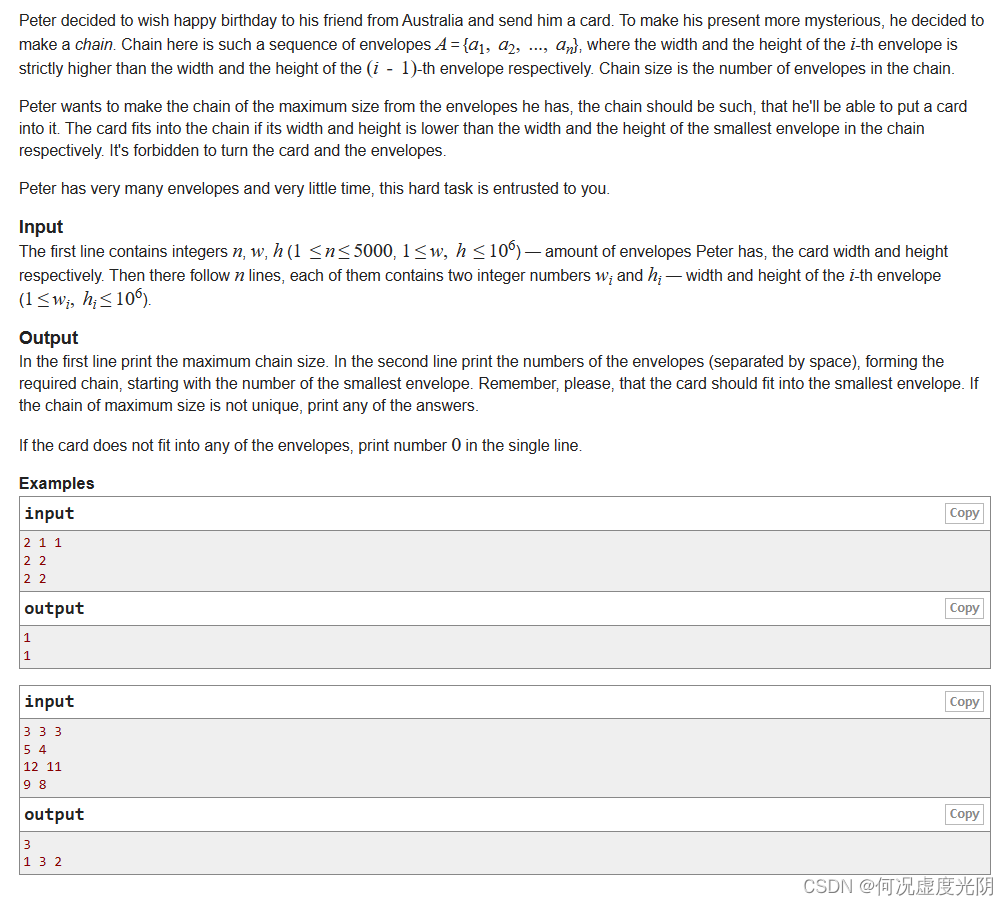
题目大意
给定 n n n 个信封的长和宽,以及一张卡片的长和宽,要求选出最多的信封,并且这些信封的长和宽都比前面的信封要大,并且最小的信封能够装下这张卡片。输出这些信封的数量和编号。
思路分析
考虑到这是一道动态规划题目,我们需要先对原问题进行拆分。具体而言,我们需要找到最长的一个信封序列
s
s
s,满足条件:
s
s
s 中的信封数最大;
s
s
s 中的所有信封的长和宽都比其前面的信封要大;
s
s
s 中最小的信封能够装下这张卡片。
我们设
d
p
[
i
]
dp[i]
dp[i] 表示以第
i
i
i 个信封结尾的最长信封序列长度。可以得到转移方程:
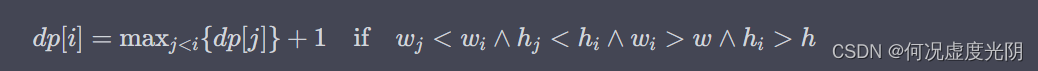
其中 w i w_i wi 和 h i h_i hi 分别是第 i i i 个信封的长和宽。
接下来,只需要在 d p dp dp 数组中寻找最大的值,即为所求的答案。为了输出方便,我们在转移的过程中,记下每个状态对应的决策节点 p r e [ i ] pre[i] pre[i],表示以第 i i i 个信封结尾的最长信封序列的前一个节点的编号。在 d p dp dp 数组的遍历过程中,一边更新 d p [ i ] dp[i] dp[i],一边更新 p r e [ i ] pre[i] pre[i]。这样,我们只需要从 d p dp dp 数组中的最大值开始,反向遍历 p r e pre pre 数组,就能得到构成最长信封序列的信封的编号。
时间复杂度:
O
(
n
2
)
O(n^2)
O(n2)。
AC代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5222;
int dp[N],f[N];
struct node{
int x,y,z;
}a[N];
bool cmp (node a,node b){
return a.x<b.x;
}
void find(int x){
if(f[x]!=-1) find(f[x]);
if(f[x]!=-1) cout<<" ";
cout<<a[x].z;
}
signed main(){
int n,xx,yy;
cin>>n>>xx>>yy;
for(int i=1;i<=n;i++){
cin>>a[i].x>>a[i].y;
a[i].z=i;
}
sort(a+1,a+n+1,cmp);
int j;
for(int i=1;i<=n;i++){
if(a[i].x<=xx||a[i].y<=yy){
dp[i]=0;
}
else {
dp[i]=1;
f[i]=-1;
for(j=1;j<i;j++){
if(dp[j]==0) continue;
if(a[j].x<a[i].x&&a[j].y<a[i].y&&dp[j]+1>dp[i]){
dp[i]=dp[j]+1;
f[i]=j;
}
}
}
}
int ans=0;
for(int i=1;i<=n;i++){
if(dp[i]>ans){
ans=dp[i];
j=i;
}
}
if(ans==0){
cout<<"0\n";
return 0;
}
else {
cout<<ans<<'\n';
find(j);
cout<<"\n";
}
}