BM38-在二叉树中找到两个节点的最近公共祖先

news2024/9/20 8:36:08

题目

给定一棵二叉树(保证非空)以及这棵树上的两个节点对应的val值 o1 和 o2，请找到 o1 和 o2 的最近公共祖先节点。

数据范围：树上节点数满足 1≤n≤10^5 , 节点值val满足区间 [0,n)

要求：时间复杂度 O(n)

注：本题保证二叉树中每个节点的val值均不相同。

如当输入{3,5,1,6,2,0,8,#,#,7,4},5,1时，二叉树{3,5,1,6,2,0,8,#,#,7,4}如下图所示：

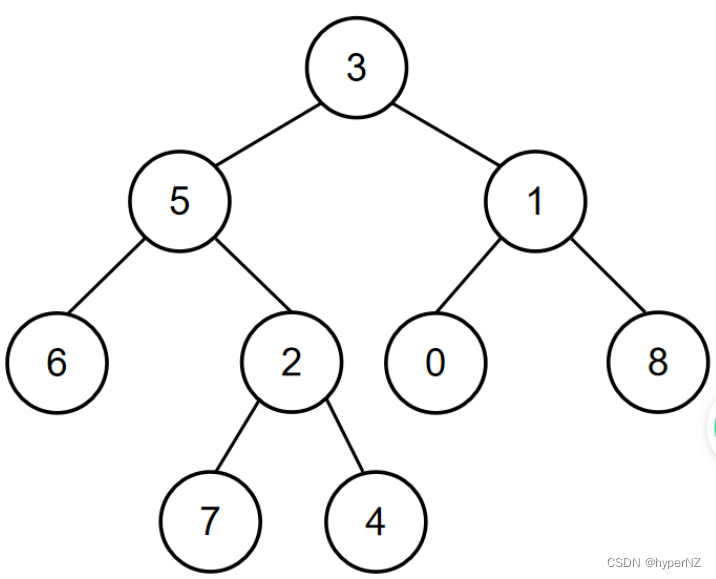
所以节点值为5和节点值为1的节点的最近公共祖先节点的节点值为3，所以对应的输出为3。

节点本身可以视为自己的祖先。

示例1

输入：{3,5,1,6,2,0,8,#,#,7,4},5,1

返回值：3

示例2

输入：{3,5,1,6,2,0,8,#,#,7,4},2,7

返回值：2

思路1：非递归写法

要想找到两个节点的最近公共祖先节点，可以从两个节点往上找，每个节点都往上走，一直走到根节点，那么根节点到这两个节点的连线肯定有相交的地方，如果是从上往下走，那么最后一次相交的节点就是他们的最近公共祖先节点。

层序遍历二叉树（BFS），记录遍历到的每个节点的父节点，存储在Map中，当两个节点o1，o2都遍历到为止。
从o1节点开始一直到根节点，记录o1节点和它的祖先节点的值，存入ancestors中。
查看o1节点和它的祖先节点是否包含o2节点，如果不包含再看是否包含o2节点的父节点......
第一次包含的节点，即是o1和o2的公共祖先节点。

代码1

import java.util.*;

/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 * }
 */

public class Solution {
    /**
     *
     * @param root TreeNode类
     * @param o1 int整型
     * @param o2 int整型
     * @return int整型
     */
    public int lowestCommonAncestor (TreeNode root, int o1, int o2) {
        //记录遍历到的每个节点的父节点存入Map中
        Map<Integer, Integer> parent = new HashMap<>();
        //队列作为辅助
        Queue<TreeNode> queue = new LinkedList<>();
        //先将根节点存入Map和queue中
        parent.put(root.val, Integer.MIN_VALUE); //根节点没有父节点，给它默认一个值
        queue.add(root);

        //直到两个节点都找到为止
        while (!parent.containsKey(o1) || !parent.containsKey(o2)) {
            //队列是一边进一边出，这里poll方法是出队
            TreeNode node = queue.poll();
            if (node.left != null) {
                //左子节点不为空，记录下它的父节点
                parent.put(node.left.val, node.val);
                //左子节点不为空，把它加入到队列中
                queue.add(node.left);
            }
            //右节点同上
            if (node.right != null) {
                parent.put(node.right.val, node.val);
                queue.add(node.right);
            }
        }

        Set<Integer> ancestors = new HashSet<>();
        //记录下o1和它的祖先节点，从o1节点开始一直到根节点
        while (parent.containsKey(o1)) {
            ancestors.add(o1);
            o1 = parent.get(o1);
        }
        //查看o1和它的祖先节点是否包含o2节点，如果不包含再看是否包含o2的父节点……
        while (!ancestors.contains(o2)) {
            o2 = parent.get(o2);
        }
        //最先相交的节点即是o1和o2的最近公共祖先节点
        return o2;
    }
}

时间复杂度：O（n），n是二叉树节点的个数，最坏情况下每个节点都会被访问一遍。
空间复杂度：O（n），一个是BFS需要的队列，一个是父子节点关系的map。

思路2：递归写法

代码2

import java.util.*;

/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 * }
 */

public class Solution {
    /**
     *
     * @param root TreeNode类
     * @param o1 int整型
     * @param o2 int整型
     * @return int整型
     */
    public int lowestCommonAncestor(TreeNode root, int o1, int o2) {
        return helper(root, o1, o2).val;
    }

    public TreeNode helper(TreeNode root, int o1, int o2) {
        if (root == null || root.val == o1 || root.val == o2) {
            return root;
        }

        TreeNode left = helper(root.left, o1, o2);
        TreeNode right = helper(root.right, o1, o2);

        //如果left为空，说明这两个节点在root结点的右子树上，只需要返回右子树查找的结果即可
        if (left == null) {
            return right;
        }
        //同上
        if (right == null) {
            return left;
        }
        
        //如果left和right都不为空，说明这两个节点一个在root的左子树上，一个在root的右子树上，只需要返回cur结点即可。
        return root;
    }
}