1. 本文讲述的是匈牙利算法，即图论中寻找最大匹配的算法。
2. 解决的问题是从二分图中找到尽量多的匹配。

原题-华为-HJ28 素数伴侣

描述
题目描述
若两个正整数的和为素数，则这两个正整数称之为“素数伴侣”，如2和5、6和13，它们能应用于通信加密。现在密码学会请你设计一个程序，从已有的 N （ N 为偶数）个正整数中挑选出若干对组成“素数伴侣”，挑选方案多种多样，例如有4个正整数：2，5，6，13，如果将5和6分为一组中只能得到一组“素数伴侣”，而将2和5、6和13编组将得到两组“素数伴侣”，能组成“素数伴侣”最多的方案称为“最佳方案”，当然密码学会希望你寻找出“最佳方案”。

输入:

有一个正偶数 n ，表示待挑选的自然数的个数。后面给出 n 个具体的数字。

输出:

输出一个整数 K ，表示你求得的“最佳方案”组成“素数伴侣”的对数。

数据范围： 1≤n≤100 ，输入的数据大小满足 2≤val≤30000
输入描述：
输入说明
1 输入一个正偶数 n
2 输入 n 个整数

输出描述：
求得的“最佳方案”组成“素数伴侣”的对数。

示例1
输入：
4
2 5 6 13
输出：
2

示例2
输入：
2
3 6
输出：
0

解题

1. 判断和是否是素数
2. 进行最佳最多的匹配实现配对
3. 两数必定是一偶一奇数
4. 把输入的数字进行判断分成奇偶两组
5. 若一组为空说明无法组成
6. 之后通过匈牙利算法实现最多匹配

#include<iostream>
#include<vector>
using namespace std;

bool isprime(int num){ //判断一个数是否是素数
    for(int i = 2; i * i <= num; i++){ //遍历到根号num
        if(num % i == 0) //检查有无余数
            return false;
    }
    return true;
}

bool find(int num, vector<int>& evens, vector<bool>& used, vector<int>& match){
    for(int i = 0; i < evens.size(); i++){ //遍历每个偶数与奇数比较
        if(isprime(num + evens[i]) && !used[i]){
            used[i] = true;
            if(match[i] == 0 || find(match[i], evens, used, match)){ //如果第i个偶数还未配对，或者跟它配对的奇数还有别的选择
                match[i] = num; //则配对该数
                return true;
            }
        }
    }
    return false;
}
int main(){
    int n;
    while(cin >> n){
        vector<int> odds;
        vector<int> evens;
        vector<int> nums(n);
        for(int i = 0; i < n; i++){ //输入n个数
            cin >> nums[i];
            if(nums[i] % 2) //奇数
                odds.push_back(nums[i]);
            else //偶数
                evens.push_back(nums[i]);
        }
        int count = 0;
        if(odds.size() == 0 || evens.size() == 0){ //缺少奇数或者偶数无法构成素数
            cout << count << endl;
            continue;
        }
        vector<int> match(evens.size(), 0); //统计每个偶数的配对是哪个奇数
        for(int i = 0; i < odds.size(); i++){ //遍历每个奇数
            vector<bool> used(evens.size(), false); //每一轮偶数都没用过
            if(find(odds[i], evens, used, match)) //能否找到配对的偶数，且要最优
                count++;
        }
        cout << count << endl;
    }
    return 0;
}

匈牙利算法

二分图如下：

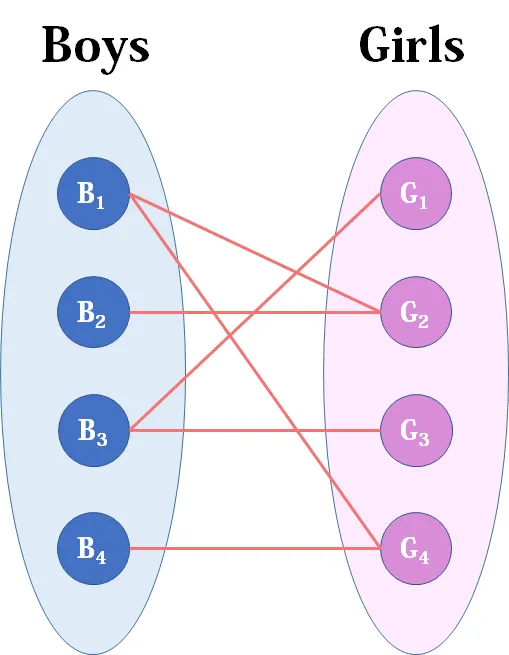
你是红娘，可以撮合任何一对有暧昧关系的男女，那么你最多能成全多少对情侣？（数学表述：在二分图中最多能找到多少条没有公共端点的边）

思路：如何成全一个男的和另外两个女的暧昧，

• 情况1：其中一个女A有其他暧昧对象，另外一个女B没有暧昧对象，优先撮合男的和女B，反之亦然;如果A的另外一个暧昧对象C还有一个暧昧对象D，那么C和D成也行和A成也行都是最优。
• 情况2：A有其他暧昧对象，B也有其他暧昧对象，考虑排在前的
• 情况3：A和B没有有暧昧对象，考虑排在前的

简单来说就是，让只有一个暧昧对象的先成，再考虑渣男渣女
代码如下：

int M, N;            //M, N分别表示左、右侧集合的元素数量
int Map[MAXM][MAXN]; //邻接矩阵存图
int p[MAXN];         //记录当前右侧元素所对应的左侧元素
bool vis[MAXN];      //记录右侧元素是否已被访问过
bool match(int i)
{
    for (int j = 1; j <= N; ++j)
        if (Map[i][j] && !vis[j]) //有边且未访问
        {
            vis[j] = true;                 //记录状态为访问过
            if (p[j] == 0 || match(p[j])) //如果暂无匹配，或者原来匹配的左侧元素可以找到新的匹配
            {
                p[j] = i;    //当前左侧元素成为当前右侧元素的新匹配
                return true; //返回匹配成功
            }
        }
    return false; //循环结束，仍未找到匹配，返回匹配失败
}
int Hungarian()
{
    int cnt = 0;
    for (int i = 1; i <= M; ++i)
    {
        memset(vis, 0, sizeof(vis)); //重置vis数组
        if (match(i))
            cnt++;
    }
    return cnt;
}