Data Preprocessing
- 前言
- Why preprocess?
- Major Tasks in Data Preprocessing
- Data Cleaning
- Incomplete (Missing) Data
- What to Consider When Handling Missing Data?
- MCAR
- MAR
- MNAR
- How to Handle Missing Data - Imputation
- More on Imputation
- Even More on Imputation
- Preprocessing and Evaluation
- Conclusion
- Noisy Data
- Handling Noisy Data
- Data Transformation and Data Discretization
- Data Transformation
- Normalization
- Discretization
- Discretization Methods
- Binnning (在Tutorial中出现过)
- Discretization by Correlation Analysis
- Correlation Analysis
- Discretization by Correlation Analysis
- Imbalanced Data
- Sampling the data
- Cluster-Based Oversampling
- SMOTE - Synthetic Minority Oversampling Technique (Chawla et al. 2002)
- Data Reduction
- Dimensionality Reduction
- Principal Component Analysis - PCA (重点)
- PCA approaches
- PCA - steps
- Feature or Attribute Selection
- Feature Selection using Correlation
- Heuristic Search in Attribute Selection
- Relief - Instance-based heuristic for feature selection (在Tutorial中出现过)
- Relief Example
- Relief summary
- Wrappers
- Preprocessing
- Conclusion
前言
本文将基于UoA的课件介绍机器学习中的数据预处理。
涉及的英语比较基础,所以为节省时间(不是full-time,还有其他三门课程,所以时间还是比较紧的),只在我以为需要解释的地方进行解释。
此文不用于任何商业用途,仅仅是个人学习过程笔记以及心得体会,侵必删。
We will cover:
Data Cleaning
Missing Data
Preprocessing and Evaluation
Data Reduction
Noisy Data
Data Transformation and Data Discretization
Imbalanced Data
Why preprocess?
 we will…
we will…

Major Tasks in Data Preprocessing

Data Cleaning

Incomplete (Missing) Data

What to Consider When Handling Missing Data?
MCAR
缺失完全随机指的是缺失数据的出现与数据本身完全无关,缺失数据的出现没有任何模式或规律,纯粹是随机发生的。完全无关于数据指的是缺失数据与数据本身之间没有任何关联或联系,缺失数据的出现对数据的分析和解释没有影响。
 潜在的问题可能出现在样本量较小的情况下,因为缺失数据的样本量较少,可能对结果的可靠性和泛化性产生影响。
潜在的问题可能出现在样本量较小的情况下,因为缺失数据的样本量较少,可能对结果的可靠性和泛化性产生影响。
MAR
缺失随机指的是缺失数据的出现与缺失数据本身有关,但是与缺失数据所在的行或样本无关,与其他数据的观测值有关。缺失数据的出现和其他数据的观测值之间有关系,也就是说,缺失数据和其他数据有一定的相关性或联系。
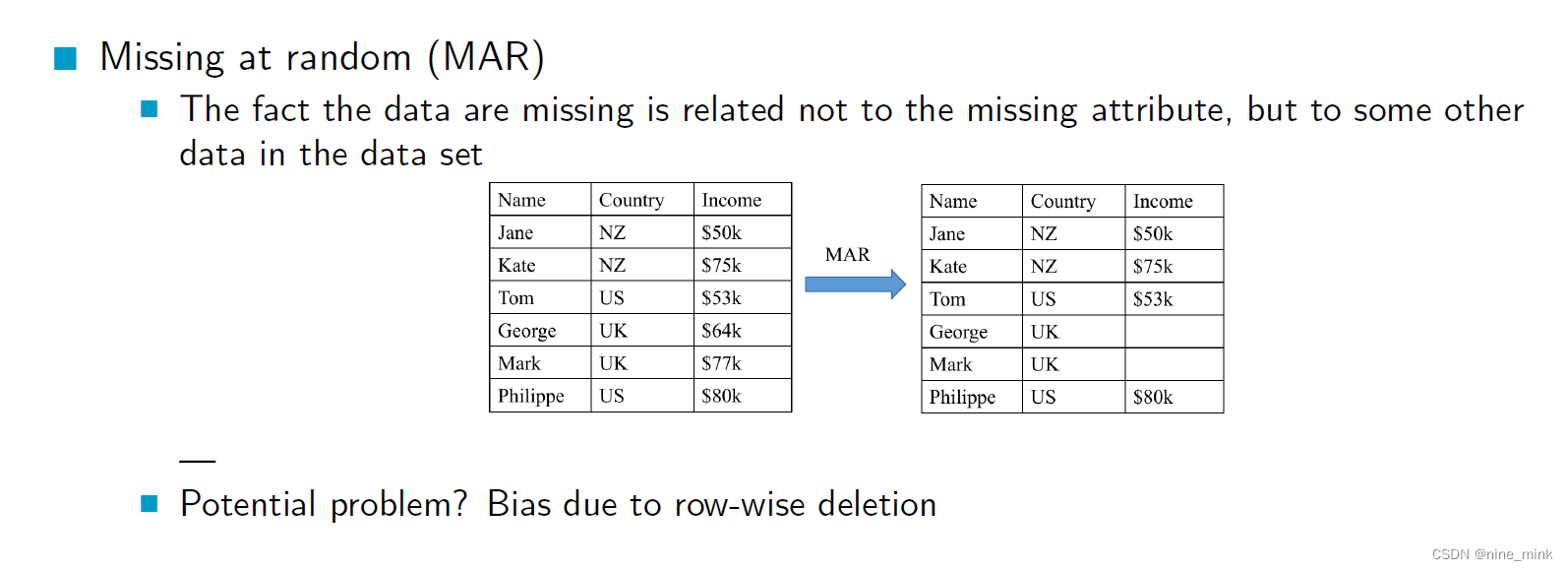 潜在的问题可能出现在行删除方式的情况下,因为行删除方式可能会导致样本偏差,即删除了某些缺失值较多或者某些特定属性的数据,从而影响结果的可靠性和泛化性。
潜在的问题可能出现在行删除方式的情况下,因为行删除方式可能会导致样本偏差,即删除了某些缺失值较多或者某些特定属性的数据,从而影响结果的可靠性和泛化性。
MNAR
非随机缺失指的是缺失数据的出现与缺失数据本身有关,与其他数据的观测值无关,缺失的原因是与变量本身相关的。比如说,某些人不愿意透露自己的财产状况,导致财产数据出现缺失。
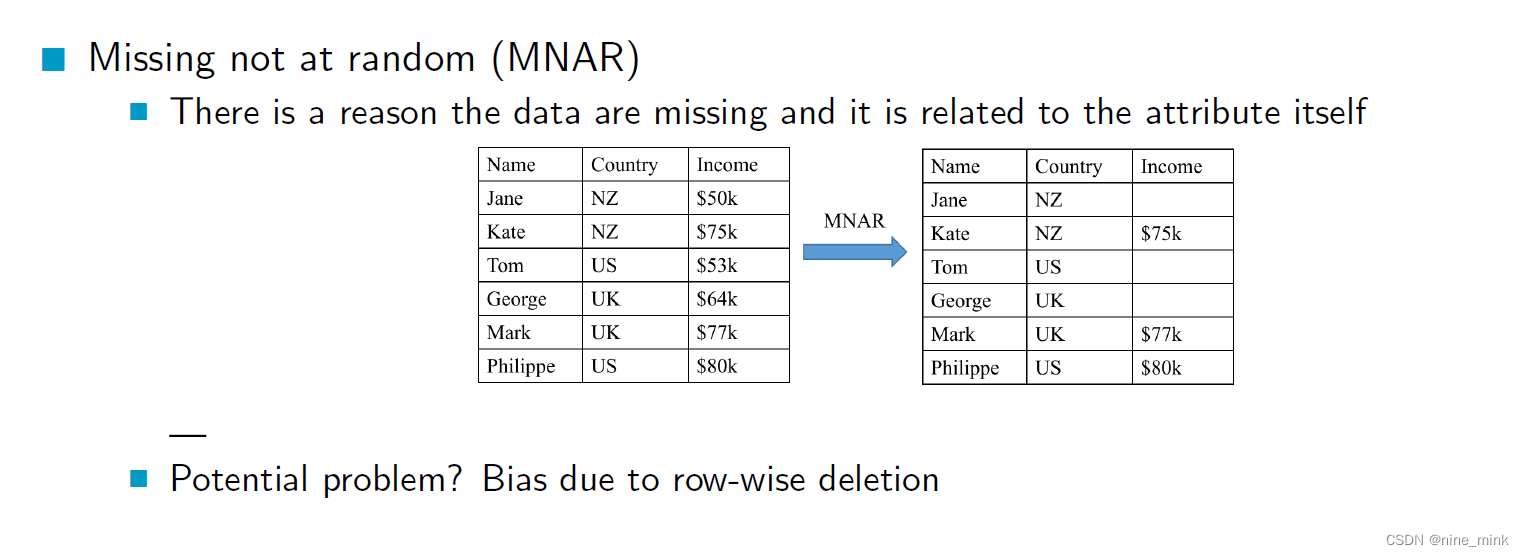 潜在的问题可能出现在行删除方式的情况下,因为行删除方式可能会导致样本偏差,即删除了某些缺失值较多或者某些特定属性的数据,从而影响结果的可靠性和泛化性
潜在的问题可能出现在行删除方式的情况下,因为行删除方式可能会导致样本偏差,即删除了某些缺失值较多或者某些特定属性的数据,从而影响结果的可靠性和泛化性
How to Handle Missing Data - Imputation
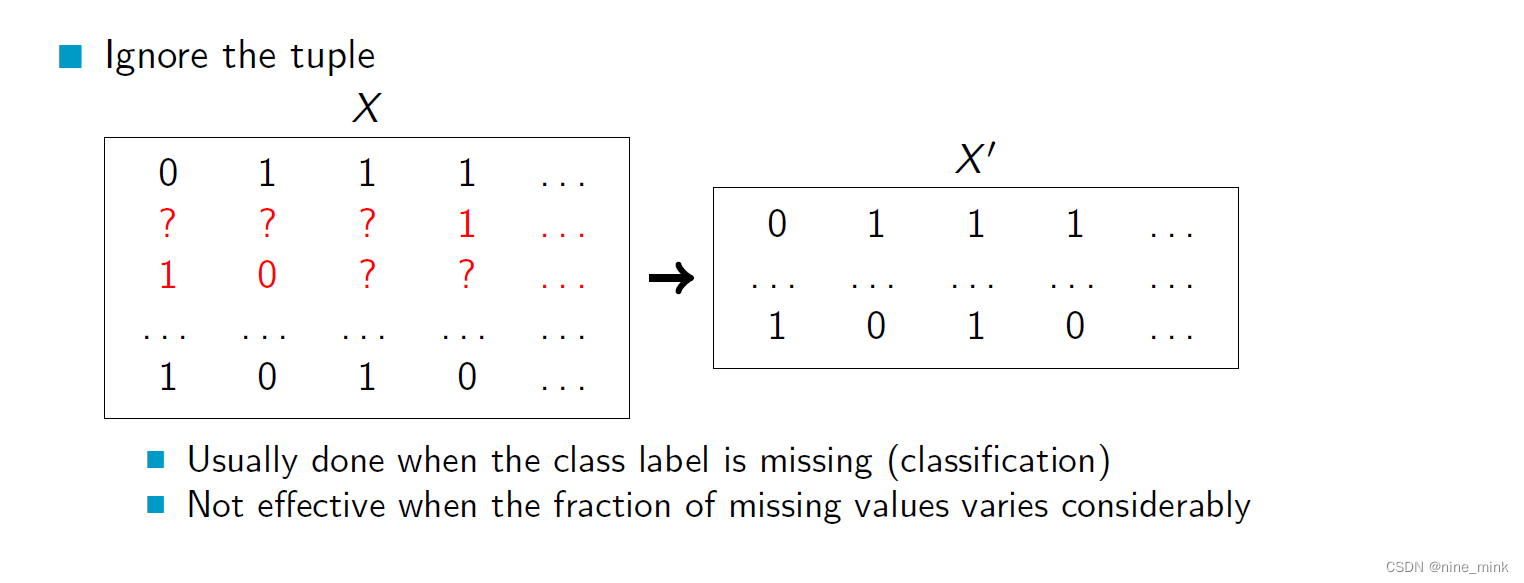
当某一行数据缺失了类别标签(classification)时,我们通常会采取这种方法来处理。具体操作就是将该行数据直接从数据集中删除。但是这种方法并不适用于缺失值的数量变化很大的情况。在这种情况下,忽略元组的效果会受到影响。
当数据中存在缺失值时,我们可以通过人工的方式来填充这些缺失值,使得数据变得完整。但是这种方法通常比较繁琐,而且有时候可能并不可行,尤其当缺失值较多时。

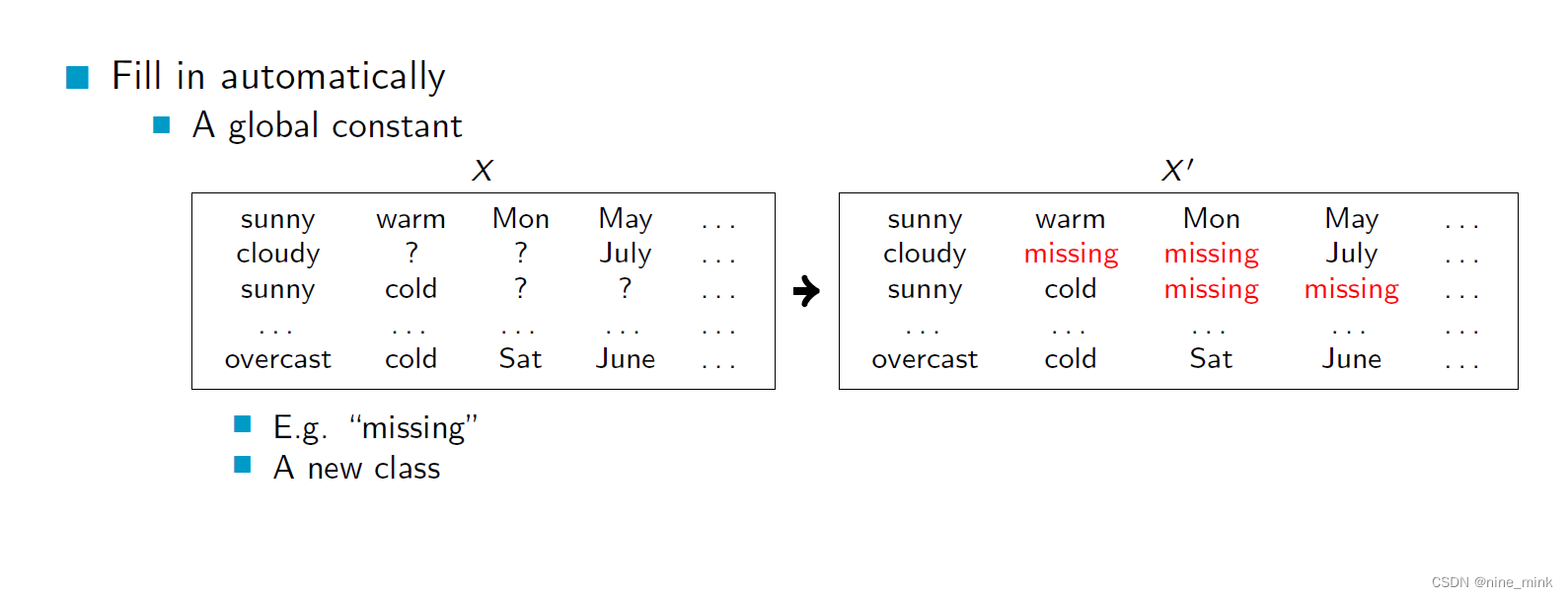
当数据中存在缺失值时,我们可以使用一些默认值或者新的类别来自动填充这些缺失值,使得数据变得完整。例如,可以使用一个全局的常量值来填充缺失值,或者将缺失值划分为一个新的类别,表示这些数据的特殊性质。
另一种方法是使用该属性的平均值来代替缺失值。这种方法通常由许多软件自动完成,但会改变与其他变量的关系,可能会引入偏差。
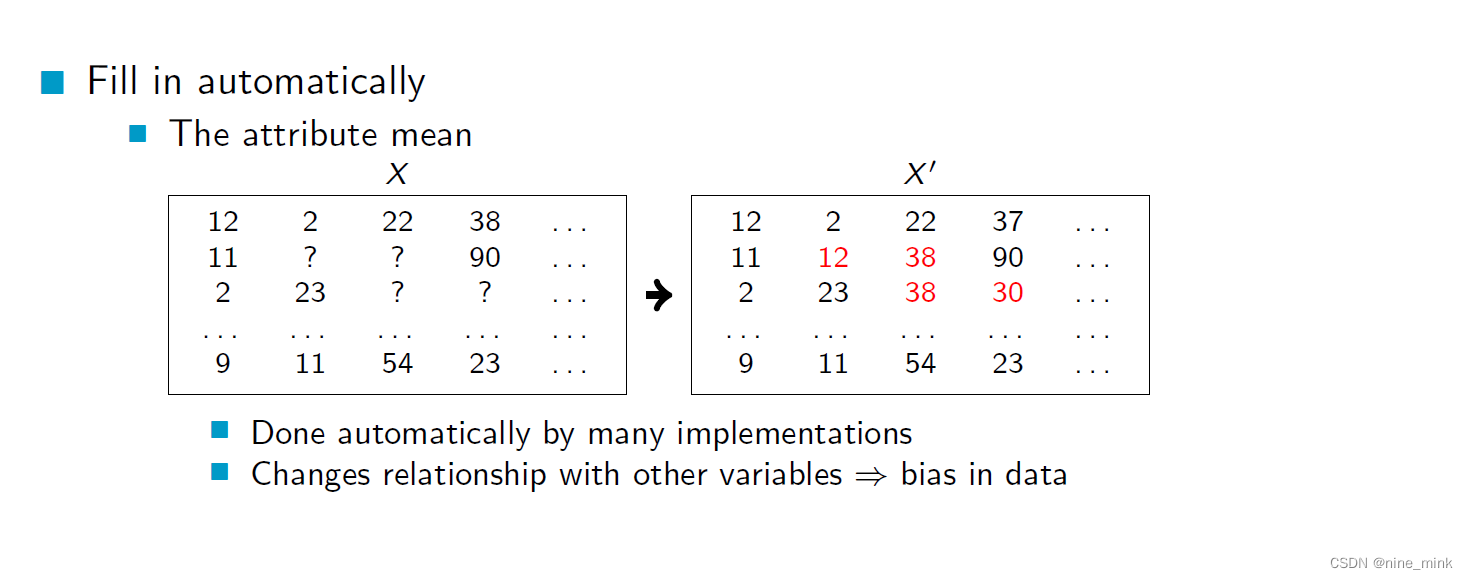
在同一类别下的样本中,对于缺失的属性值进行填充,使用的值是该类别下所有样本该属性的平均值。这个方法的优点是可以保持类别内部的一致性,缺点是可能会导致与其他属性之间的关系发生改变,导致数据偏
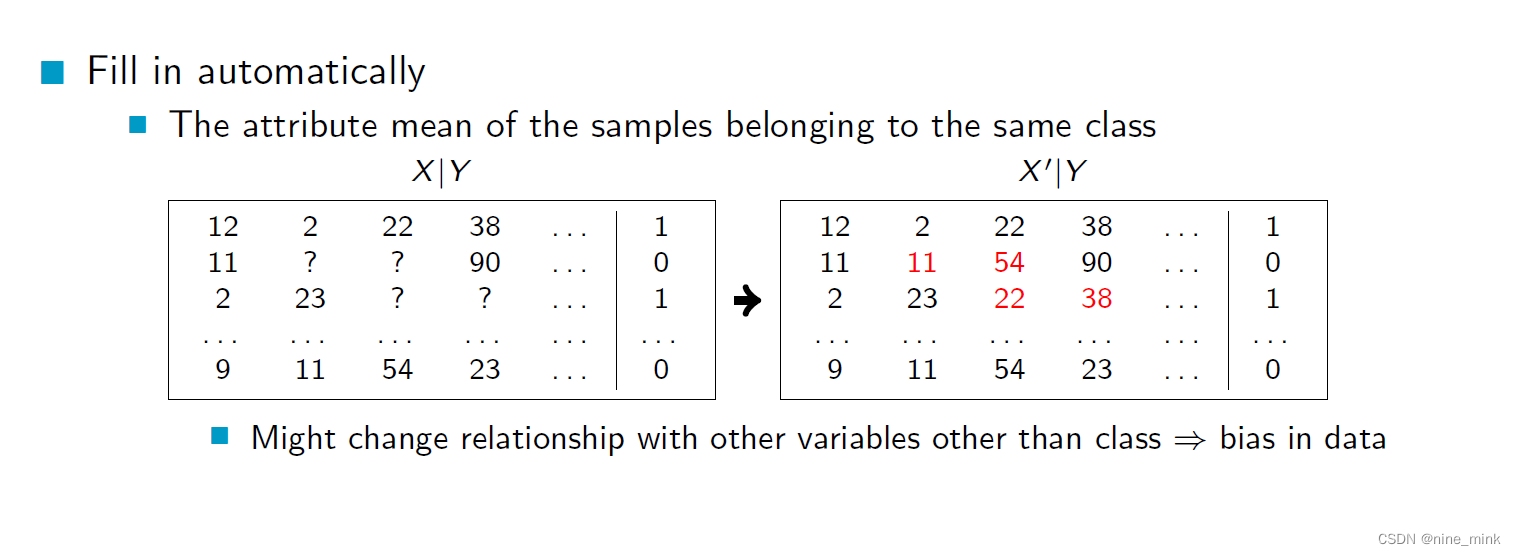
这个方法是使用基于推断的算法,比如贝叶斯公式、决策树、最近邻等自动填充缺失值。具体来说,通过使用这些算法,从已有的数据中找到最有可能的值来填充缺失的数据。这种方法可以根据已有的数据和模型的推断能力来进行填充,但也可能因为模型的不准确性而导致填充结果不准确。
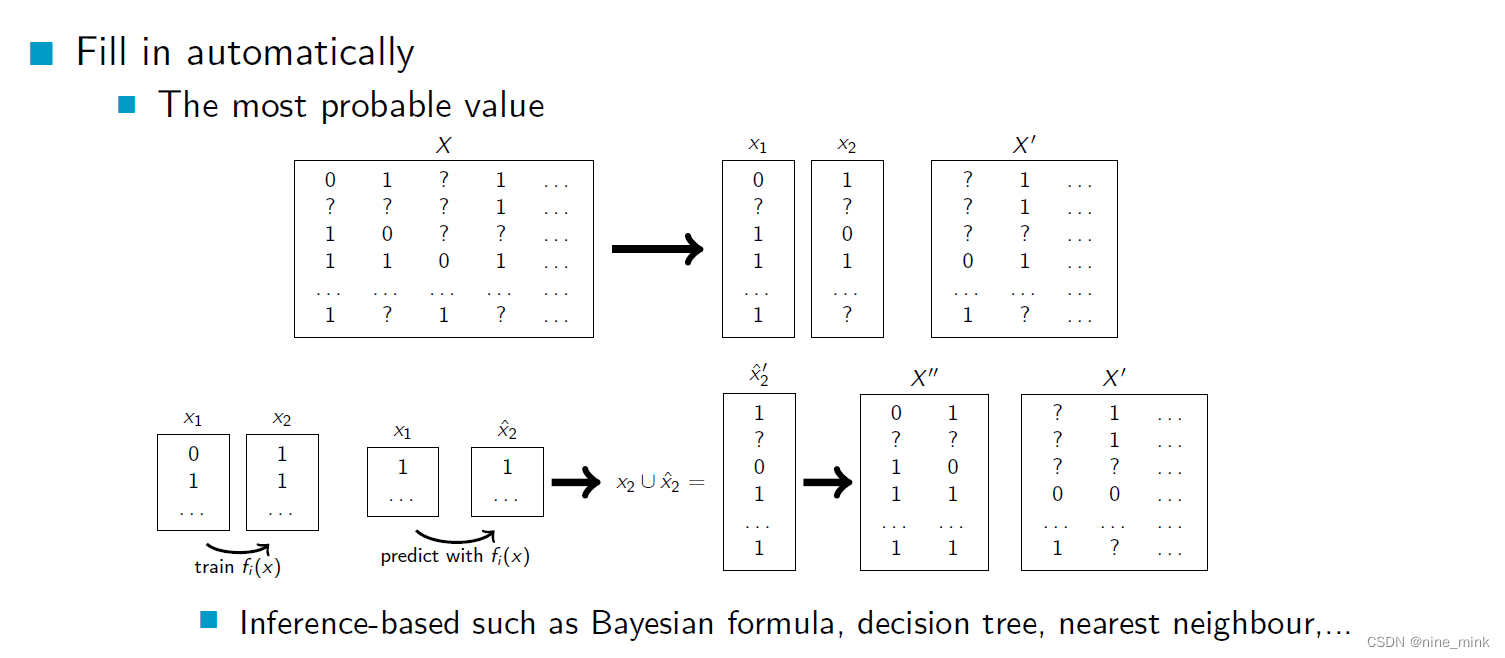
More on Imputation
矩阵分解方法,例如奇异值分解,可以将数据矩阵X分解为X=UVT的形式。通过将U和VT相乘,可以创建插补矩阵X0。例如,可以在矩阵X中插入一些缺失值,并通过分解矩阵X来估算这些缺失值,最小化估算值与实际值之间的平方误差。分解矩阵X会得到三个矩阵U、和VT,其中U和VT包含每个样本的隐含特征,是奇异值矩阵。插补矩阵X0的值是通过乘以矩阵U、和VT的转置得到的。

Even More on Imputation
 EM插补是一种使用其他变量的值来估算缺失值的方法。它包含两个步骤:期望步骤(Expectation)和最大化步骤(Maximization)。
EM插补是一种使用其他变量的值来估算缺失值的方法。它包含两个步骤:期望步骤(Expectation)和最大化步骤(Maximization)。
在期望步骤中,使用适当的模型(例如分类器或回归模型)来预测缺失值。这些预测值会作为估算值,用于填充缺失值。
在最大化步骤中,检查估算值是否是最可能的值。这可以通过比较估算值与其他可能的值来实现,选择最可能的值作为最终的填充值。
多次插补(例如MICE)是一种重复使用期望步骤和最大化步骤的方法,通常会重复3-5次。在完成多次插补后,可以进行所需的完整数据分析,例如构建分类器和评估模型性能。
最后,平均估算值或评估结果是通过多次插补得到的,作为最终的插补值或评估结果。
没有一种通用的最佳方法,选择合适的插补方法取决于数据的性质、缺失值的分布以及分析的目标。不同的方法在不同情况下可能会有不同的效果,需要根据具体情况选择合适的方法。
Preprocessing and Evaluation
 在数据评估中,预处理步骤的位置通常取决于具体的预处理方法,例如插补(imputation)。
在数据评估中,预处理步骤的位置通常取决于具体的预处理方法,例如插补(imputation)。
对于插补这个例子,有几种可能的做法:
-
在将数据集划分为训练集和测试集之前进行插补:这意味着在进行数据集划分之前,先对整个数据集进行插补处理,包括训练集和测试集。然后,再将数据集划分为训练集和测试集,并在划分后的数据集上进行后续的评估和建模。
-
只在训练集中进行插补:这意味着只对训练集进行插补处理,不对测试集进行插补。这样做的目的是模拟在实际应用中,模型只能根据训练集中的信息进行预测,而无法访问测试集中的真实值。然后,在训练集上进行建模和评估,并将模型应用于未插补的测试集上进行评估。
对于这两种做法,没有固定的规则,应该根据具体情况和预处理方法的性质来选择。例如,如果插补方法涉及使用训练集中的信息来填充缺失值,并且这些信息对测试集的预测可能有影响,那么在训练集和测试集之前都进行插补可能是更合适的做法。如果插补方法不依赖于训练集中的信息,或者对测试集的预测没有影响,那么只在训练集中进行插补也可以是一个合理的选择。在选择预处理步骤的位置时,应该考虑数据的性质、预处理方法的性质以及评估的目标,确保在进行评估和建模时使用合适的数据处理方法。
Conclusion

Noisy Data

Handling Noisy Data
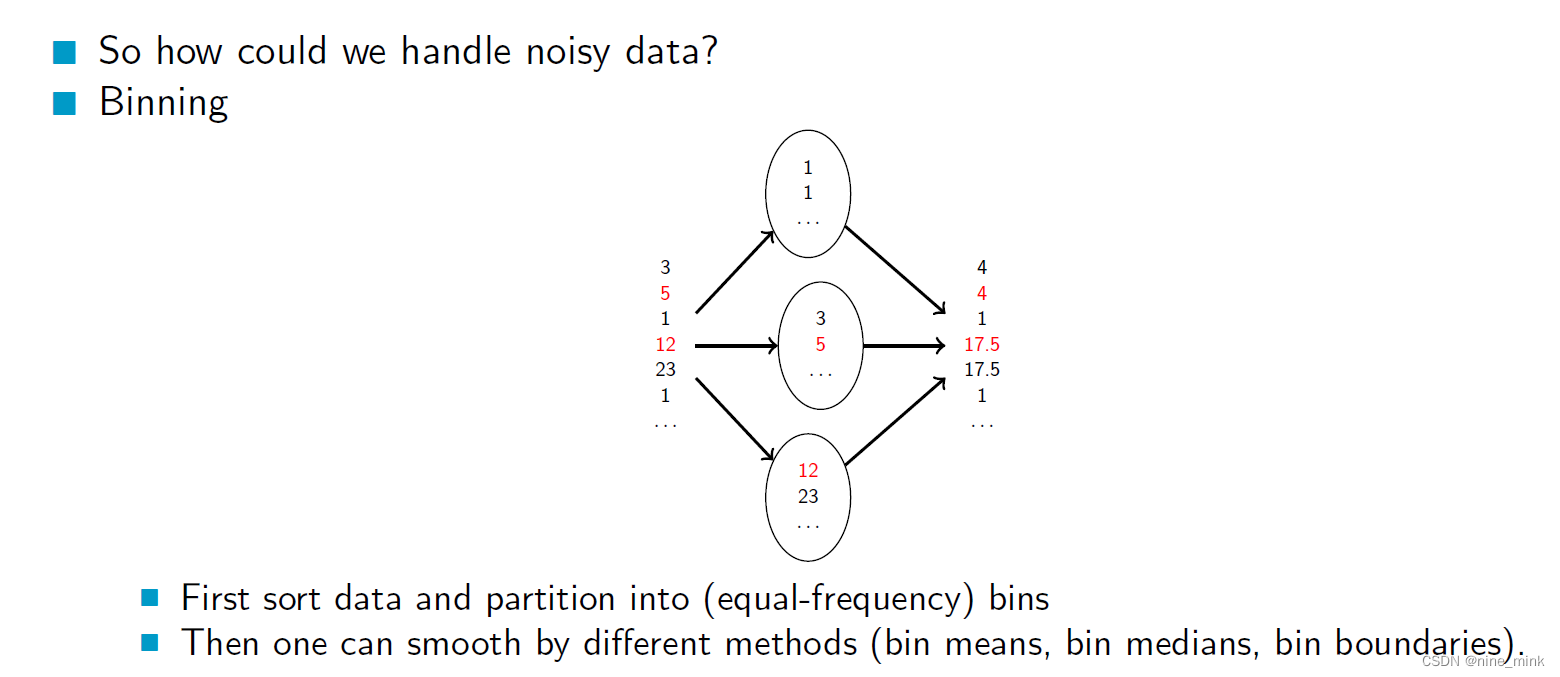
Binning是一种将连续的数值变量离散化为有序的类别变量的方法。将数据分成几个桶(bins),每个桶代表一个数值区间。这可以减少数据中的噪声或随机误差对分析的影响,因为将数据离散化可以使数据更加平滑,并使分析更容易。
通过将连续数据划分为有限数量的类别,Binning可以减少数据集中的噪声和不必要的复杂性。例如,将数据集中的温度值划分为“低温”,“中温”和“高温”,可以在不失去太多信息的情况下简化数据。然后,我们可以在每个类别中计算出统计信息,例如平均值和标准差,以更好地理解数据。

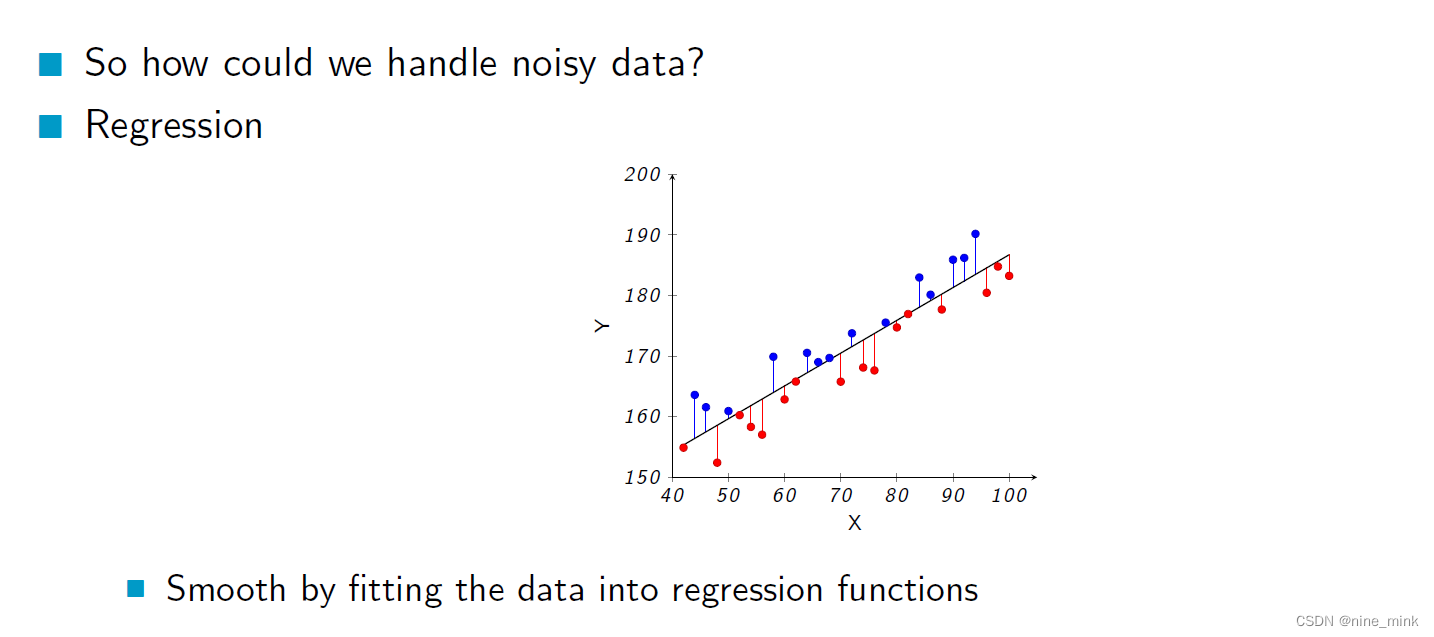
在回归分析中,可以通过拟合一个数学模型来描述自变量和因变量之间的关系,并且通过分析模型的拟合程度来评估这种关系的强度。当数据中存在噪声时,即存在一些随机误差或变异性,回归分析可以通过将这些噪声纳入模型中,进而将其纠正或降低其影响,从而提高模型的拟合程度和预测能力
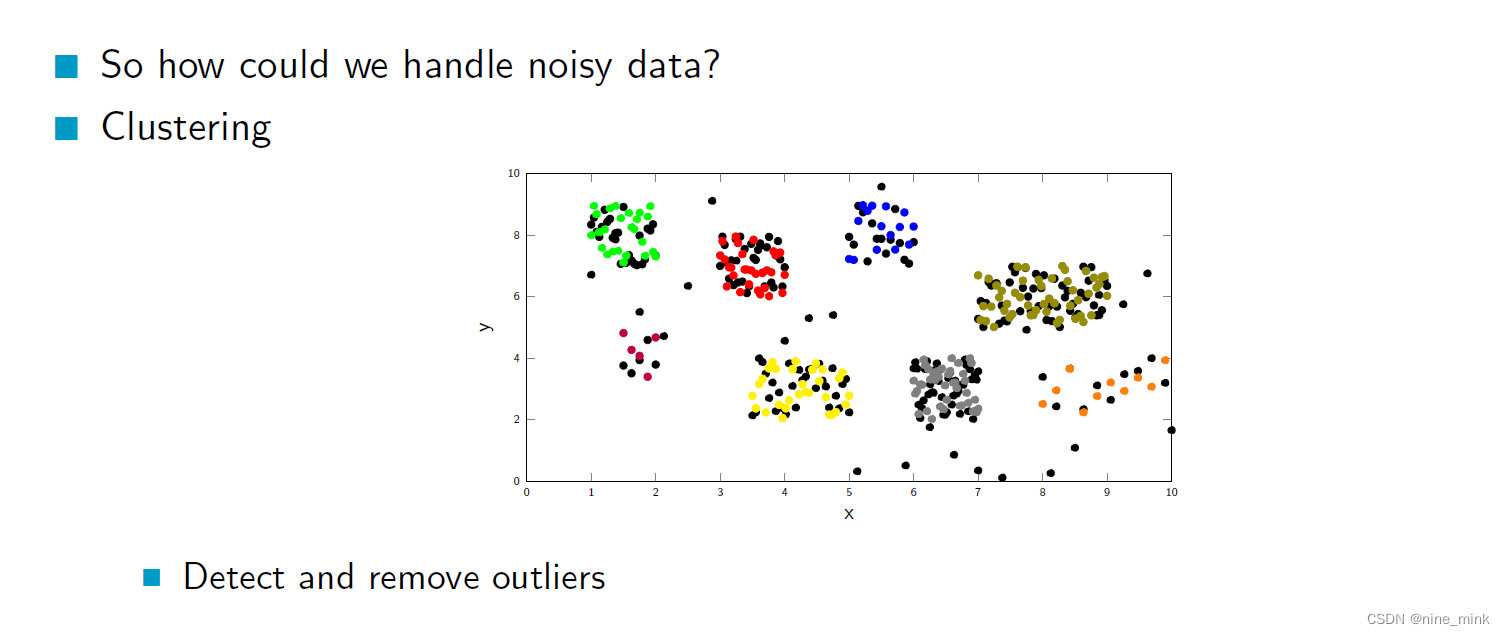
聚类可以被介绍为一种处理Nosy的方法,因为它可以用于发现数据集中的异常值或离群点。在聚类过程中,算法会将相似的数据点归为一类,并尝试识别与其他点不同的点。
如果一个数据点与其它数据点很不相似,那么它有可能是一个异常值或离群点。聚类算法可以将这些点分为它们自己的簇中,使得它们更容易被识别和处理。
此外,聚类还可以用于探索数据集的结构,识别潜在的模式和关系,这也有助于发现Nosy数据并进行处理。
Data Transformation and Data Discretization
Data Transformation
数据转换是指将一个属性的所有值映射到一个新的取值集合,每个旧的值对应一个新的值。数据转换的方法包括:平滑、属性/特征构建、归一化和离散化等。平滑可以去除数据中的噪声,属性/特征构建可以从给定的属性中构建出新的属性,归一化可以将数据缩放到指定的范围内,常用的归一化方法有最小-最大归一化、Z-score归一化和十进制标度归一化。离散化则是通过概念层次上升将连续属性转换为离散属性。

Normalization
归一化(Normalization)是一种数据转换方法,将属性的值域映射到一个新的范围内,以便更好地处理和比较不同的属性。归一化的方法有多种,其中包括最小最大归一化、Z-score归一化和十进制缩放归一化等。最小最大归一化将数据映射到新的最小值和最大值之间,Z-score归一化使用均值和标准差对数据进行归一化,十进制缩放归一化通过使属性的值除以某个数量级的幂次,使得所有值都在[-1, 1]之间。

Discretization
离散化是将连续属性的值域划分为间隔的过程。通过离散化,可以将实际数据值替换为间隔标签。离散化可以递归地应用于属性,有助于减小数据量和为进一步分析做准备,例如分类。得到的挖掘模式通常更易于理解,并可以在不同数据抽象级别(概念层次结构)上进行挖掘。属性类型有三种:名义属性(来自无序集合的值,例如颜色),序数属性(来自有序集合的值,例如排名)和数值属性(实数,例如整数或实数)。

Discretization Methods
离散化方法可以根据其处理方式和使用类别信息的方式进行分类。
-
自上而下 vs 自下而上(处理方式):自上而下的离散化方法从整体范围开始,逐步划分为子范围;而自下而上的离散化方法从单个数据点开始,逐步合并为更大的范围。
-
监督式 vs 非监督式(类别信息使用方式):监督式离散化方法使用类别信息来指导离散化过程,而非监督式离散化方法则不考虑类别信息。
一些常见的离散化方法包括:
- Binning(自上而下划分,非监督式):将数据范围划分为固定数量或固定宽度的间隔。
- 直方图分析(自上而下划分,非监督式):基于数据的分布情况,将数据划分为不同的间隔。
- 聚类分析(非监督式,可以是自上而下划分或自下而上合并):利用聚类算法将数据点分组为不同的簇,然后将簇作为离散化的间隔。
- 决策树分析(监督式,自上而下划分):利用决策树算法根据类别信息来划分数据范围。
- 相关性分析(监督式,自下而上合并):根据属性之间的相关性来合并数据范围。

Binnning (在Tutorial中出现过)

等宽离散化是一种将数据离散化为区间的方法,可以按照区间的数量将数据划分为等宽的N个区间,每个区间的宽度为数据的范围除以区间数。这种方法比较简单,但是对于有些数据不太适用,例如数据分布不均匀或者存在离群值的情况。等深离散化则是将数据划分为包含相同数量样本的N个区间,这种方法更适用于数据分布不均匀的情况,但是对于分类属性的处理较为棘手。
Discretization by Correlation Analysis
 基于相关性分析的离散化方法,如Chi-merge,是一种利用类别信息进行离散化的方法。它采用了自底向上的合并策略,找到具有相似类别分布(即低卡方值)的相邻区间进行合并。合并操作会递归地进行,直到满足预定义的停止条件。这种方法可以在离散化过程中考虑类别信息,从而提高离散化的准确性和效果。
基于相关性分析的离散化方法,如Chi-merge,是一种利用类别信息进行离散化的方法。它采用了自底向上的合并策略,找到具有相似类别分布(即低卡方值)的相邻区间进行合并。合并操作会递归地进行,直到满足预定义的停止条件。这种方法可以在离散化过程中考虑类别信息,从而提高离散化的准确性和效果。
Correlation Analysis
 相关性分析是用来衡量两个变量之间相关性的一种方法。在这里,我们考虑两个名义变量 C 和 B,它们分别有 k 和 r 种取值。使用 χ2 检验可以计算它们之间的相关性:
相关性分析是用来衡量两个变量之间相关性的一种方法。在这里,我们考虑两个名义变量 C 和 B,它们分别有 k 和 r 种取值。使用 χ2 检验可以计算它们之间的相关性:
χ2 = ∑∑ (oij − eij)2 / eij
其中 oij 是事件 (ci, bj) 的实际频率,eij 是期望频率,n 是实例数量。期望频率 eij 通过以下方式计算:
eij = (count(C = ci) × count(B = bj)) / n
χ2 越大,说明两个变量越不可能独立。
Discretization by Correlation Analysis
使用 Chi-merge 方法进行离散化是一种基于 χ2 统计量的方法,它利用了类别信息。它采用自底向上的合并策略,通过找到相邻的区间(其类别分布相似,即 χ2 值较低)来合并区间。合并是递归进行的,直到满足预定义的停止条件为止。这种方法可以根据类别信息帮助选择合适的离散化边界,从而在离散化过程中考虑了类别分布的影响。


Imbalanced Data
当数据不平衡时,一些类别的样本数量比其他类别多很多。这可能会导致评估问题,因为分类器可能会倾向于预测样本数量更多的类别,导致对较少类别的预测效果较差。例如,如果类别1的样本比类别0多很多,则分类器可能会过度预测类别1,导致类别0的预测效果较差。
解决这个问题的方法之一是重新采样。一种方法是欠采样,即从样本数量更多的类别中随机选择一些样本,以使两个类别的样本数量相等。另一种方法是过采样,即增加样本数量较少的类别的样本数量,直到两个类别的样本数量相等。还可以使用一些组合方法,例如SMOTE算法,生成一些合成的样本来增加样本数量较少的类别。此外,可以使用不同的评估指标,例如精确度-召回率和ROC曲线,来评估分类器的性能。

Sampling the data
数据采样是一种通过增加或减少特定类别的样本数量来调整数据集的方法,以改善分类器对少数类别的预测效果。
欠采样是从样本数量较多的类别中随机选择一些样本,使两个类别的样本数量相等或接近相等。这可以通过随机删除多数类别的样本来实现,从而平衡数据集。但是,这样做可能会导致丢失重要信息,并引入偏差。
过采样是从样本数量较少的类别中随机添加更多的样本,以增加其样本数量,从而使两个类别的样本数量相等或接近相等。这样做可以避免信息丢失,但可能会导致过拟合问题,因为添加的样本可能过于相似。
除了随机采样外,还有一些替代方法。例如,可以使用基于SMOTE(合成少数类过采样技术)的方法,通过生成合成的少数类样本来增加其样本数量。还可以使用集成学习方法,如集成采样和集成欠采样,以平衡数据集并提高分类器性能。这些方法可以根据具体情况选择,以改善对不平衡数据的处理效果。

Cluster-Based Oversampling
聚类过采样是一种通过将正类和负类样本独立地分成不同的簇(或者群组),然后对每个独立的簇应用过采样或欠采样技术的方法。
聚类过采样的优势在于可以在样本之间建立更丰富的关系,从而更好地保留了样本之间的数据分布信息。这样做可以避免传统的随机过采样可能导致的样本相似性过高的问题,从而减少了过拟合的风险。
然而,聚类过采样本身并不一定解决过拟合问题,因为在某些情况下,仍然可能存在过采样导致的样本重复和噪声问题。因此,在应用聚类过采样时,仍然需要谨慎地选择合适的聚类算法和采样策略,以确保在处理过拟合问题时取得良好的效果。

SMOTE - Synthetic Minority Oversampling Technique (Chawla et al. 2002)
 SMOTE(合成少数类过采样技术)是一种生成新的人工样本的方法,用于解决类别不平衡的问题。
SMOTE(合成少数类过采样技术)是一种生成新的人工样本的方法,用于解决类别不平衡的问题。
SMOTE的处理过程如下:
- 找到少数类样本中最近的一对实例(通过计算在少数类样本中的欧氏距离或其他距离度量方法),这两个实例被称为"合成样本"的"种子"。
- 在这两个种子样本之间创建一个新的合成样本。这个合成样本的特征值是在两个种子样本之间的线性插值。
- 将新合成的样本添加到少数类样本中,使得它们被归类为少数类。
SMOTE的目标是通过合成新的少数类样本来平衡类别不平衡的数据集,从而增加少数类样本的数量,提高分类器对少数类的预测性能。然而,需要注意的是,生成的合成样本可能会引入一定的噪声和不确定性,因此在应用SMOTE时需要谨慎选择合适的参数和策略,以确保取得良好的效果。
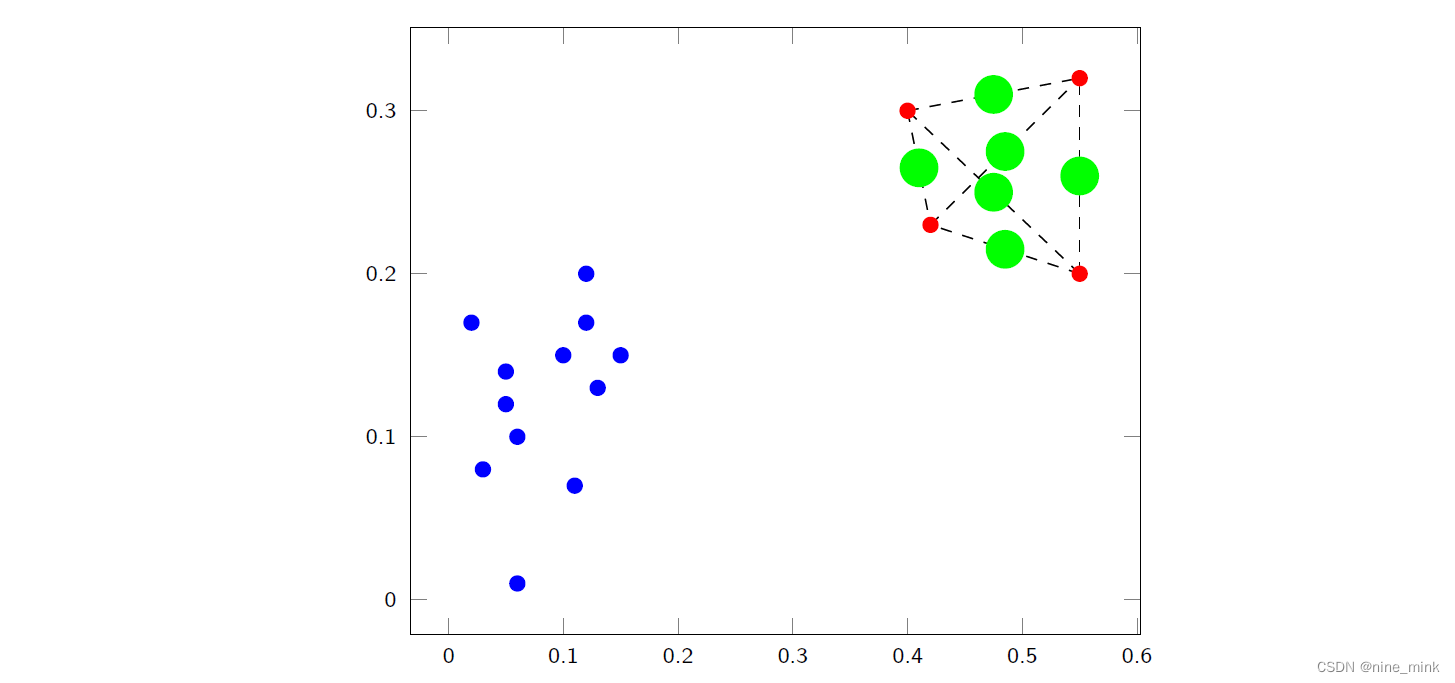
Data Reduction
数据压缩是一种数据减少的策略,目的是获取一个数据集的简化版本,这个版本的体积小得多,但产生的分析结果与原数据集相同或几乎相同。为什么要进行数据减少呢?因为一个数据库可能存储着数千兆字节的数据,对这些数据进行复杂的数据分析可能需要很长时间。数据减少的策略有很多种,比如维度减少、小波变换、主成分分析(PCA)、特征选择、数量缩减、回归和对数线性模型、直方图、聚类、抽样和数据压缩。

Dimensionality Reduction
在高维数据中,数据变得越来越稀疏,点之间的密度和距离变得越来越不具有代表性。这被称为维数灾难。维数灾难的发生会影响到聚类、异常检测、分类和回归等任务的精度和效率。因此,为了解决这个问题,我们需要进行降维处理,使得数据变得更加紧密,同时保留重要的特征信息,以便后续的分析和挖掘。常见的降维技术有主成分分析(PCA)、线性判别分析(LDA)和t-SNE等。


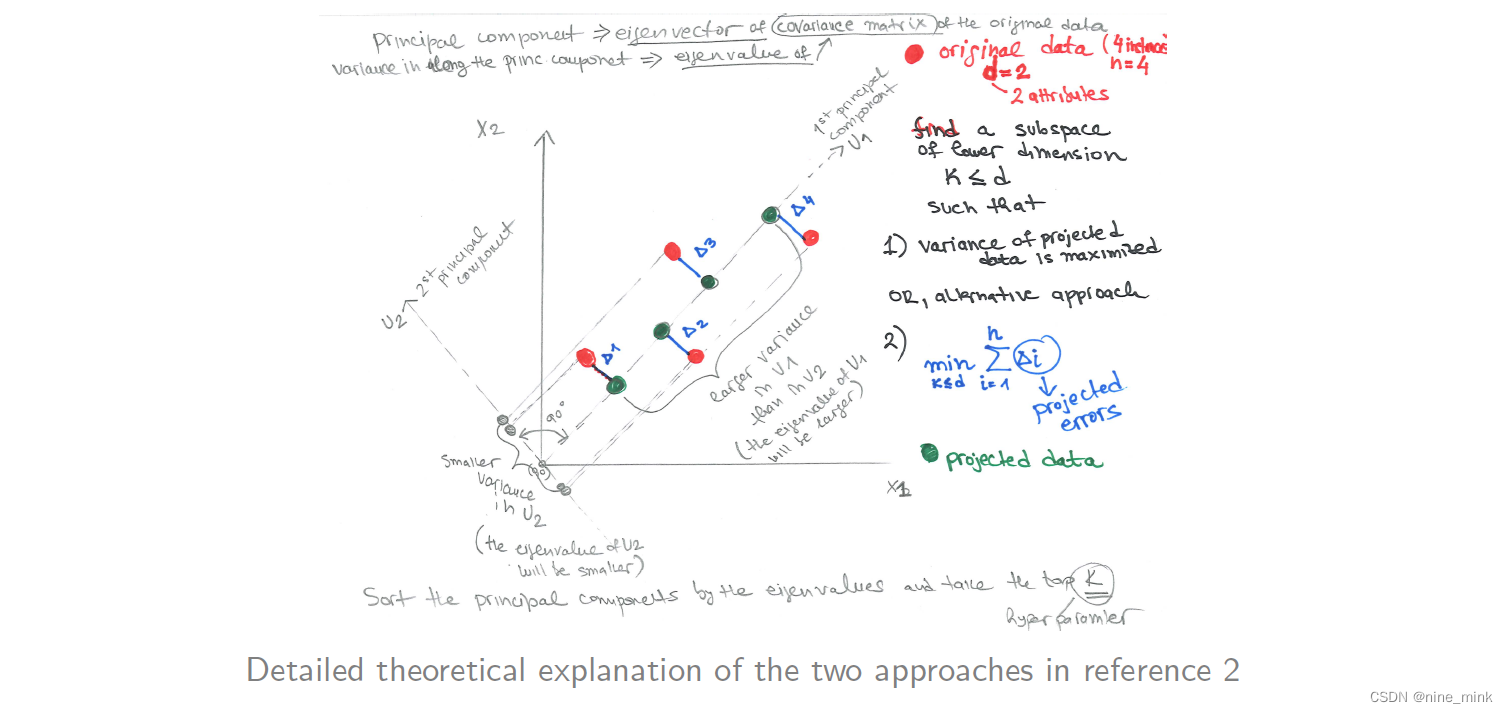
Principal Component Analysis - PCA (重点)
主成分分析(PCA)是一种降维技术,它通过找到能够捕捉数据中最大变化的投影来将原始数据投影到一个较小的空间中。具体而言,我们会计算输入属性的协方差矩阵的特征向量和特征值。特征向量表示数据变化的方向,它们定义了新的属性空间;而特征值表示沿着相应特征向量的方向上的方差的大小。通过选择具有最大特征值的特征向量,我们可以将数据投影到一个更低维度的空间,从而实现数据的降维。这样做可以减少数据的复杂性,同时保留了大部分的信息。

PCA approaches
PCA - steps
 PCA 的步骤如下:
PCA 的步骤如下:
- 归一化输入数据:把每个属性放到相同的尺度上;
- 计算 k 个正交的特征向量,也就是主成分;
- 输入数据是 k 个主成分的线性组合;
- 主成分按照重要性排序,也就是按照方差来排,方差越大的主成分越重要;
- 保留前 d-k 个最重要的主成分,舍弃剩下的弱主成分;
- 最后得到的主成分是互不相关的向量。
PCA 可以用在数值型数据和分类型数据上。
Feature or Attribute Selection
特征选择是通过移除一组属性来降低维度的方法。
- 冗余属性:一个或多个属性中包含大部分或全部信息,是多余的。例如,产品购买价格和支付的销售税金额。
- 不相关属性:包含对当前数据挖掘任务无用的信息。例如,学生的ID对预测学生GPA的任务通常是无关的。
有两种类型的方法:过滤器(快速)和包装器(高准确性,昂贵)。
- 过滤器将特征选择与分类器学习分开。没有偏向任何学习算法。

Feature Selection using Correlation
对于名义数据,给定两个属性A和B,其值为a1, …, ac和b1, …, br,可以使用χ2检验计算相关性:
χ2 = Xc i=1 Xr j=1 (oij - eij )^2 / eij
其中oij是事件(ai, bj)的实际频率,而eij是预期频率(n是实例的数量)
eij = count(A = ai) * count(B = bj) / n
其中count(A = ai)是属性A中ai值的计数,count(B = bj)是属性B中bj值的计数。通过计算χ2值,可以衡量属性A和B之间的相关性,即它们是否可能相互依赖。如果χ2值越高,则属性A和B之间的相关性越强。在特征选择中,可以根据这种相关性来决定是否保留或删除某些属性。
 对于两个数值属性A和B,可以使用Pearson相关系数来度量它们之间的相关性。公式如下:
对于两个数值属性A和B,可以使用Pearson相关系数来度量它们之间的相关性。公式如下:
r_AB = Σ((a_i - μ_A)(b_i - μ_B)) / (n * σ_A * σ_B)
其中,a_i和b_i分别是A和B属性的实际值,μ_A和μ_B分别是A和B属性的平均值,n是实例的数量,σ_A和σ_B分别是A和B属性的标准差。
Pearson相关系数的取值范围在-1到1之间,表示两个属性之间的线性关系的强度和方向。当r_AB接近1时,表示两个属性之间存在强正相关性;当r_AB接近-1时,表示两个属性之间存在强负相关性;当r_AB接近0时,表示两个属性之间没有线性关系。如果标准差σ_A或σ_B为0,那么Pearson相关系数将未定义。通过计算Pearson相关系数,可以帮助判断数值属性A和B之间的相关性,从而在特征选择中做出相应的决策。

 相关性测量两个变量之间的关系强度和方向,取值范围为[-1,1]。如果两个变量之间具有强相关性,则它们的相关系数接近1;如果两个变量之间具有负相关性,则它们的相关系数接近于-1;如果两个变量之间没有线性关系,则它们的相关系数接近于0。相关性是评估两个变量之间是否存在某种关联或依赖关系的一种度量。
相关性测量两个变量之间的关系强度和方向,取值范围为[-1,1]。如果两个变量之间具有强相关性,则它们的相关系数接近1;如果两个变量之间具有负相关性,则它们的相关系数接近于-1;如果两个变量之间没有线性关系,则它们的相关系数接近于0。相关性是评估两个变量之间是否存在某种关联或依赖关系的一种度量。
可以使用相关性来删除冗余或不重要的特征。具有高相关性的特征可能包含相同或类似的信息,因此可以选择其中一个特征进行保留。对于不相关或低相关性的特征,则可以考虑将其删除,因为它们可能对模型的性能没有贡献。使用相关性进行特征选择可以提高模型的准确性并减少过拟合的可能性。
Heuristic Search in Attribute Selection
启发式搜索在属性选择中的应用:
在属性组合中,有2的d-1次方种可能的属性组合,这样的穷举搜索是不可行的(例如,当d = 300时,属性组合数是2.04x10^90)。因此,常见的启发式属性选择方法有:
- 在属性独立性假设下选择最佳单个属性
- 最佳逐步特征选择:首先选择最佳单个属性,然后再选择与第一个属性条件独立的最佳属性,以此类推。
- 逐步属性消除:反复消除最差的属性。
- 最佳组合属性选择和消除
- 最优分支定界:使用属性消除和回溯。

Relief - Instance-based heuristic for feature selection (在Tutorial中出现过)
Relief是一种基于实例的启发式特征选择算法,适用于二分类问题的数据集。它的输入包括具有n个实例和d个输入属性的数据集,以及要随机选择的实例数nr。该算法的步骤如下:
-
首先,对输入属性进行归一化,并创建一个包含每个属性权重wi的权重向量W,初始化为0。
-
然后,从数据集中随机选择一个实例R,并选择同类中离它最近的实例H(即近邻),以及异类中离它最近的实例M(即远邻)。
-
对于每个输入属性i,计算R和M之间的距离减去R和H之间的距离,然后将这个值添加到属性i的权重wi中。
-
重复步骤2-3共nr次,以更新所有属性的权重。
-
最后,将每个属性的权重wi除以nr,以获得最终权重,表示该属性对分类任务的重要性。
Relief算法利用实例之间的相似性来估计属性的重要性,它认为,与相邻实例之间距离差异较大的属性更可能是具有区分度的重要属性。

Relief Example
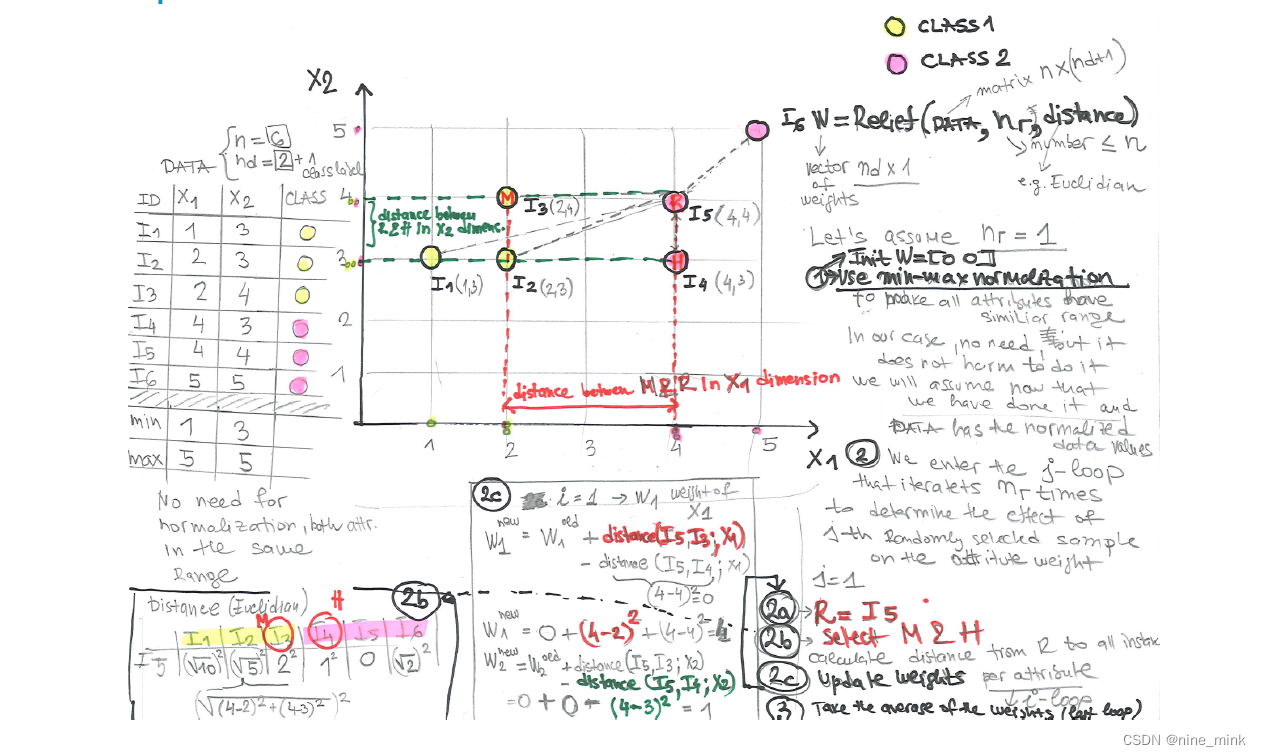

Relief summary
Relief是一种基于实例的启发式算法,用于特征选择。它考虑了所有的属性,并返回一个权重向量,表示每个特征的重要性。特征根据一个阈值或排名进行选择。上述算法是Relief的基本版本,还有各种扩展(如ReliefF、RReliefF等)。在算法中,对于每个随机选择的实例,找到与它最近的同类实例和最近的不同类实例。通过比较它们与该实例的属性值来更新每个属性的权重,权重越高表示该属性越重要。最终得到的权重向量可用于特征选择,也可以通过阈值或排序来确定选择的特征。

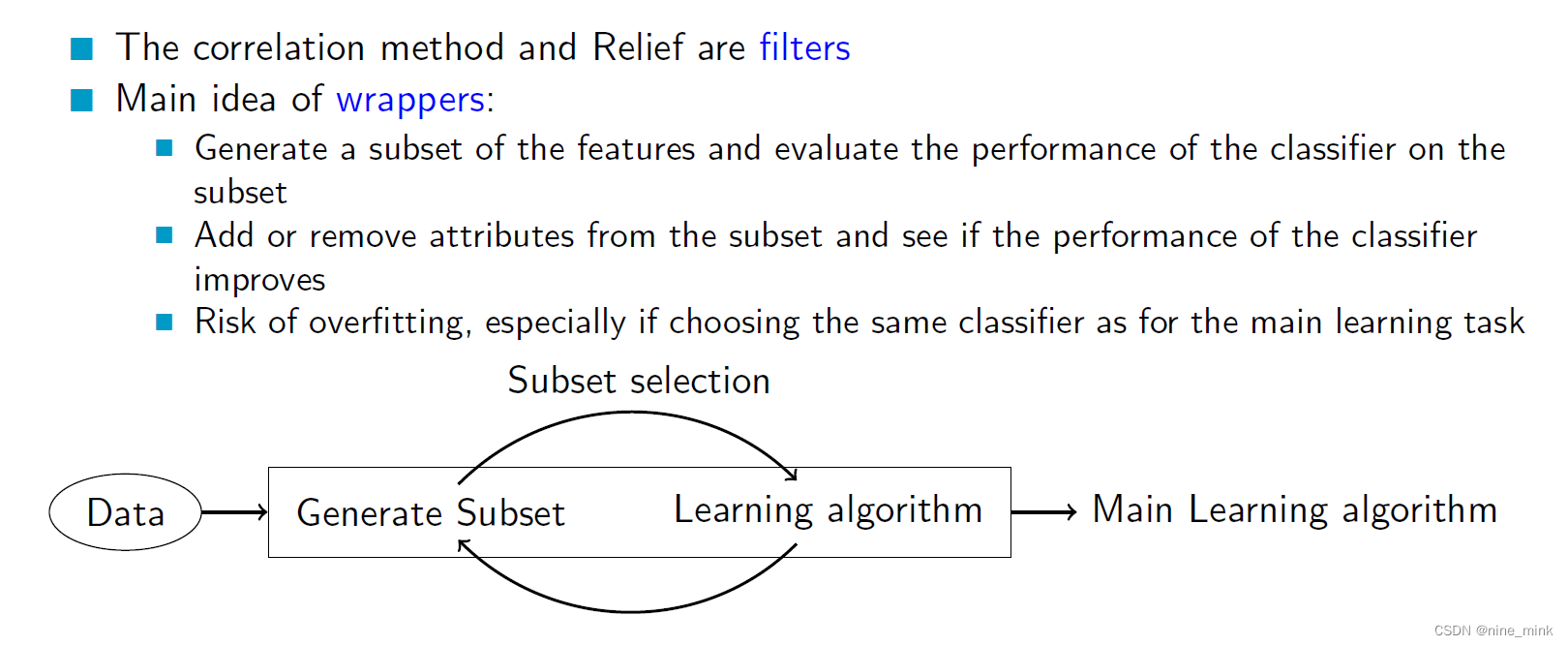
Wrappers
Wrapper方法是一种特征选择的方法,相对于过滤方法,它们可以更好地评估候选特征集的质量,因为它们使用的是实际的学习算法,而不是简单的评估函数。Wrapper方法的主要思想是生成一组特征子集,并评估分类器在这些子集上的性能。然后添加或删除特征并观察分类器的性能是否有所改善。使用Wrapper方法时需要注意过拟合问题,特别是当使用与主要学习任务相同的分类器时。
Preprocessing
 When are preprocessing approaches useful?
When are preprocessing approaches useful?
当数据集中包含许多冗余或不相关的特征时,预处理方法会很有用。预处理方法可以用于特征选择,可以缩小特征空间并提高分类器的效率和准确性。另外,如果数据集包含缺失值,预处理方法可以用来填补缺失值。
When should you avoid them?
应该避免在数据集上使用预处理方法,如果数据集非常小并且不包含冗余特征或缺失值,因为在这种情况下,预处理可能会导致过度拟合,从而影响分类器的泛化性能。
How about speci c cases
Many correlated features?
当数据集中有很多相关特征时,使用特征选择技术是很有用的。
Many independent features?
而当数据集中有许多独立特征时,特征选择方法可能没有太大的帮助,因为每个特征都提供了额外的信息。
Which algorithms you know already would need preprocessing?
许多机器学习算法都需要预处理,如KNN,支持向量机,神经网络等。
How about Decision trees? Why?
决策树不需要预处理,因为它可以自动选择重要的特征进行分割。决策树是一种自顶向下的贪婪算法,每次选择最能提高信息增益的特征进行分割。
How about Regression? Why?
回归模型通常需要特征缩放,因为回归模型基于特征的线性组合。
Are we cheating in preprocessing: for example by creating new examples?
在预处理过程中,有时会创建新的示例来填补缺失值或平衡数据集。这种方法可能会在某些情况下导致过度拟合或泛化能力降低,因此需要谨慎使用。
Conclusion
概括地说,预处理是机器学习和数据分析中非常重要的一部分。在预处理的过程中,我们需要处理缺失值、噪声数据以及进行特征选择等。对于缺失值,我们可以使用各种填充方法进行处理;对于噪声数据,我们可以使用分箱、聚类或回归等方法进行处理。特征选择可以用来减少冗余和不重要的特征。在数据不平衡的情况下,我们可以使用采样方法来解决分类器的问题。


![【LeetCode】数据结构题解(3)[查找链表中倒数第k个节点]](https://img-blog.csdnimg.cn/7d08c8c749a349baa29e524eaa2139ac.png#pic_center)