1.星座图

h = scatterplot(sqrt(sps)*txSig(sps*span+1:end-sps*span),sps,offset);
hold on
scatterplot(rxSigFilt(span+1:end-span),n,offset,'bx',h)
scatterplot(dataMod,n,offset,'r+',h)
legend('Transmit Signal','Received Signal','Ideal','location','best')

2. 眼图

Eye Diagram

Display 1000 points of the transmitted signal eye diagram over two symbol periods.

eyediagram(txSig(sps*span+1:sps*span+1000),2*sps)

3. timescope EVM

fdmmod = comm.OFDMModulator('FFTLength',256,'NumSymbols',2);

pnoise = comm.PhaseNoise('Level',-60,'FrequencyOffset',20,'SampleRate',1000);

tscope = timescope('YLabel','EVM (%)','YLimits',[0 40], ...
    'SampleRate',1000,'TimeSpanSource','Property','TimeSpan',1.2, ...
    'ShowGrid',true);

Create an EVM object. To generate a time-varying estimate of the EVM, set the AveragingDimensions property to 2.

evm = comm.EVM('MaximumEVMOutputPort',false, ...
    'ReferenceSignalSource','Input port', ...
    'AveragingDimensions',2);

modDims = info(ofdmmod)

data = randi([0 3],modDims.DataInputSize);
qpskSig = pskmod(data,4,pi/4);
txSig1 = ofdmmod(qpskSig);

data = randi([0 3],modDims.DataInputSize);
qpskSig = pskmod(data,4,pi/4);
txSig2 = ofdmmod(qpskSig);
txSig = [txSig1; zeros(112,1); txSig2];
rxSigIQimb = iqimbal(txSig,2,5);
rxSig = pnoise(rxSigIQimb);
e = evm(txSig,rxSig);
tscope(e)

rxSym = awgn(refSym,20);

Measure the EVM of the noisy signal.

[rmsEVM,maxEVM,pctEVM,numSym] = evm(refSym,rxSym)

rmsEVM = 9.8775

maxEVM = 26.8385

pctEVM = 14.9750

numSym = 1000

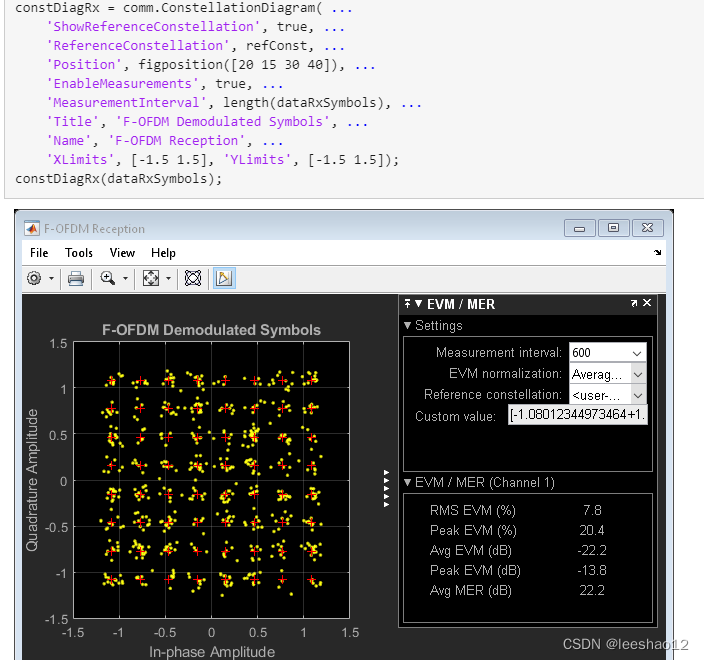
4.
% Request user input from command-line for application parameters
userInput = helperFrequencyCalibrationUserInput;

% Calculate system parameters based on the user input
[fcParam,sigSrc] = helperFrequencyCalibrationConfig(userInput);

% Create a DC blocker system object to remove the DC component of the
% received signal and increase accuracy of the frequency offset estimation.
dcBlocker = dsp.DCBlocker('Algorithm', 'Subtract mean');

% Create a coarse frequency offset estimation System Object to calculate
% the offset. The system object performs an FFT on its input signal and
% finds the frequency of maximum power. This quantity is the frequency
% offset.
CFO = comm.CoarseFrequencyCompensator( ...
    'FrequencyResolution',  25, ...
    'SampleRate',           fcParam.FrontEndSampleRate);

% Create a spectrum analyzer scope to visualize the signal spectrum
scope = dsp.SpectrumAnalyzer(...
    'Name',             'Actual Frequency Offset',...
    'Title',            'Actual Frequency Offset', ...
    'SpectrumType',     'Power',...
    'FrequencySpan',    'Full', ...
    'SampleRate',       fcParam.FrontEndSampleRate, ...
    'YLimits',          [-40,10],...
    'SpectralAverages', 50, ...
    'FrequencySpan',    'Start and stop frequencies', ...
    'StartFrequency',   -200e3, ...
    'StopFrequency',    200e3,...
    'Position',         figposition([50 30 30 40]));

5. Test and Measurement

Waveform generation, visualization, and performance analysis

Generate waveforms and use quantitative tools to measure system performance. Use graphical utilities such as constellation and eye diagrams to visualize the effects of various impairments and corrections.