目录
一, 二叉树链式实现
1. 前置说明
2. 二叉树遍历(主打的就是一个分治思想)
2. 1 前序遍历
2. 2 中序遍历
2. 3 后序遍历
2. 4 层序遍历
3. 二叉树结点个数及高度
3. 1 二叉树节点个数
3. 2 二叉树叶子节点个数
3. 3 二叉树第K层的节点个数
3. 4 二叉树查找为X的节点
3. 5 二叉树的深度
二,二叉树简单算法题
1. 965. 单值二叉树
2.100. 相同的树
3. 572. 另一棵树的子树
结语
一, 二叉树链式实现
1. 前置说明
typedef char BTDataType;
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
BTDataType data;
}BTNode;
// 结点创建
BTNode* BuyNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
printf("malloc fail\n");
exit(-1);
}
node->data = x;
node->left = node->right = NULL;
return node;
}
BTNode* CreatBinaryTree()
{
BTNode* nodeA = BuyNode('A');
BTNode* nodeB = BuyNode('B');
BTNode* nodeC = BuyNode('C');
BTNode* nodeD = BuyNode('D');
BTNode* nodeE = BuyNode('E');
BTNode* nodeF = BuyNode('F');
BTNode* nodeG = BuyNode('G');
nodeA->left = nodeB;
nodeA->right = nodeC;
nodeB->left = nodeD;
nodeB->right = nodeE;
nodeC->left = nodeF;
nodeC->right = nodeG;
return nodeA;
}构建的二叉树如图:
2. 二叉树遍历(主打的就是一个分治思想)
分治思想:将一棵大树分成多个小树。
2. 1 前序遍历
思路:分治思想,先根,再左孩子,最后右孩子。
以上面我们所创建的二叉树,来进行前序遍历结果为:
A B D NULL NULL E NULL NULL C F NULL NULL G NULL NULL
代码实现如下:
// 二叉树前序遍历
void PreOrder(BTNode* root)
{
if (root == NULL) {
printf("NULL ");
return;
}
printf("%c ", root->data);
PreOrder(root->left);
PreOrder(root->right);
}如果还是怎么清楚可以画递归图(建议多画几次):
 最后一层补充:
最后一层补充:
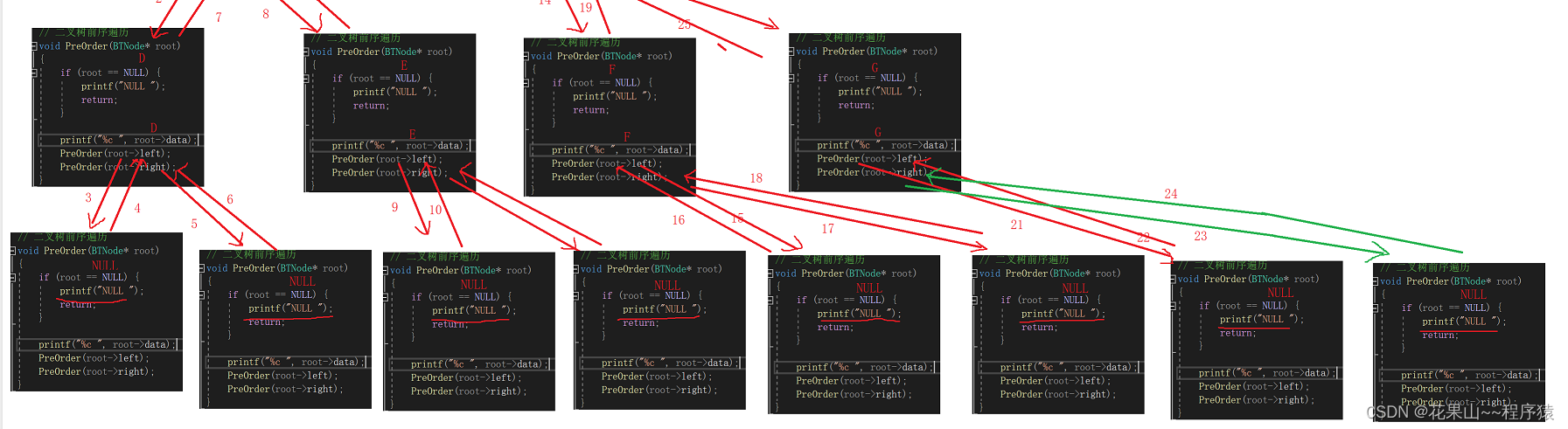
2. 2 中序遍历
思路:分治思想,先左孩子,后根,最后右孩子。
结果: NULL D NULL B NULL E NULL A NULL F NULL C NULL G NULL
代码:
// 二叉树中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%c ", root->data);
InOrder(root->right);
}如果思路不清楚,可以按照上面的递归方法进行画图。
2. 3 后序遍历
思路:分治思想,先左孩子,后右孩子,最后根。
结果: NULL NULL D NULL NULL E B NULL NULL F NULL NULL G C A
// 二叉树后序遍历
void PostOrder(BTNode* root)
{
{
if (root == NULL) {
printf("NULL ");
return;
}
PreOrder(root->left);
PreOrder(root->right);
printf("%c ", root->data);
}
}这里我们已经学完了前中后序遍历,我们会发现三种遍历法就是遍历根的时机不同造成的。
2. 4 层序遍历
层序遍历思路比较难想到,这里需要用到队列知识,需要队列的基本操作。
思路如下:
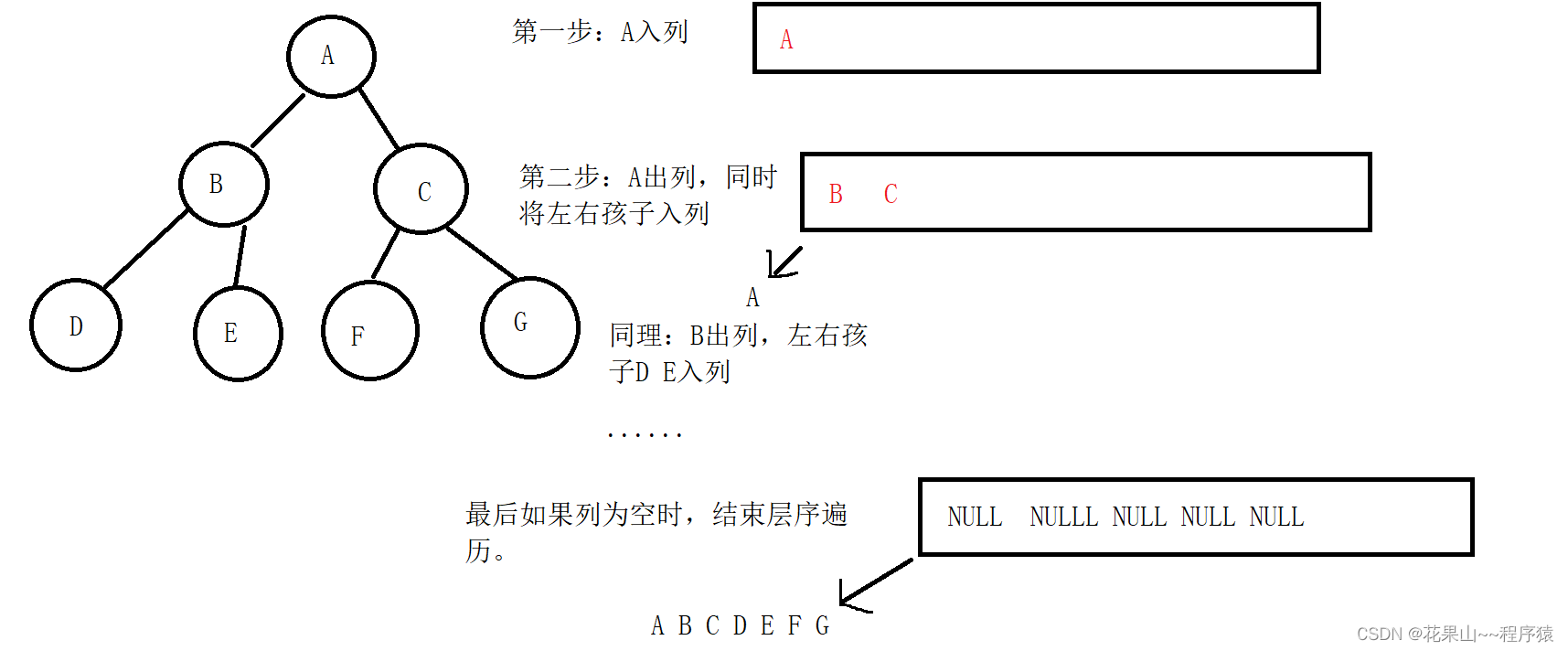
代码:
void LevelOrder(BTNode* root)
{
assert(root);
QUE my_room;
QueueInit(&my_room);
QueuePush(&my_room, root);
// 因为循环条件是队列为空
while (!QueueEmpty(&my_room))
{ // 导出队头并出列
BTNode* front = QueueFront(&my_room);
printf("%c ", front->data);
QueuePop(&my_room);
// 开始录入孩子数据
if (front->left)
{
QueuePush(&my_room, front->left);
}
if (front->right)
{
QueuePush(&my_room, front->right);
}
}
printf("\n");
QueueDestroy(&my_room);
}3. 二叉树结点个数及高度
3. 1 二叉树节点个数
思路:换一种思路, 假设我们是校长,我们要统计全校师生人数,那我会打电话给每个学院的主任他们几个主任统计的人数加起来,再加上校长本人不就是全校人数了嘛;而学院主任又会打给辅导员,让他们统计各班的人数再加上他自己,通过这样的方法不断细化,直到不能再细分为止。
以上类推可知,统计二叉树我们就只要记录每个左右孩子+ 父亲的人数即可。
代码如下:
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}3. 2 二叉树叶子节点个数
思路:如果一个根,其左右孩子都位空,那么就是叶子节点。
代码如下:
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
3. 3 二叉树第K层的节点个数
思路:在K = 1的时候,返回1即可,然后每个根统计左右孩子在K层的节点个数。
3. 4 二叉树查找为X的节点
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
if (root == NULL)
{
return 0;
}
if ( k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(root->left, k - 1)
+ BinaryTreeLevelKSize(root->right, k - 1);
}
3. 5 二叉树的深度
思路: 从根出发,我们只要保留左右孩子所返回的深度,取较大的深度然后加1(每个小树的根层)
代码如下:
// 二叉树的深度
int BinaryTreeDepth(BTNode* root)
{
if (root == NULL)
{
return 0;
}
int BTD_left = BinaryTreeDepth(root->left); // 用于保存比较,避免重新遍历
int BTD_right = BinaryTreeDepth(root->right);
return BTD_left > BTD_right ? BTD_left + 1 : BTD_right + 1;
}二,二叉树简单算法题
1. 965. 单值二叉树
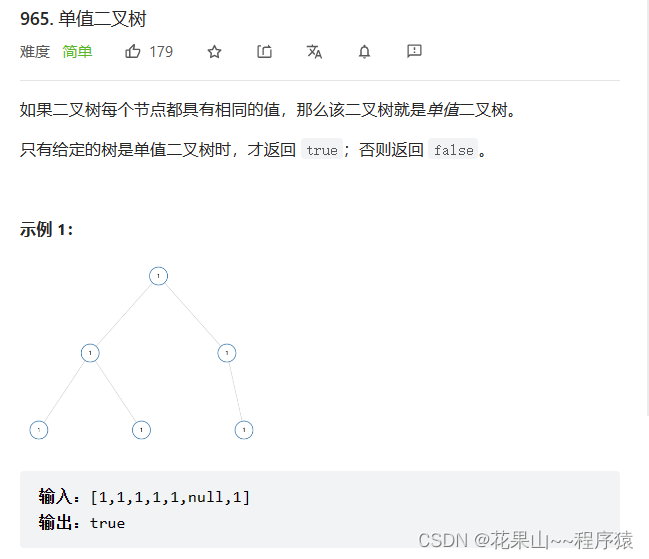
思路:从根开始判断左右孩子,是否同根相同。如果相同,返回True;反之false。 返回值必须左右孩子都为True才能表明两边根和孩子都相同。
代码如下:
bool isUnivalTree(struct TreeNode* root){
if(root == NULL)
return true;
if(root->left && root->left->val != root->val)
return false;
if(root->right && root->right->val != root->val)
return false;
return isUnivalTree(root->left) && isUnivalTree(root->right);
} 
2.100. 相同的树
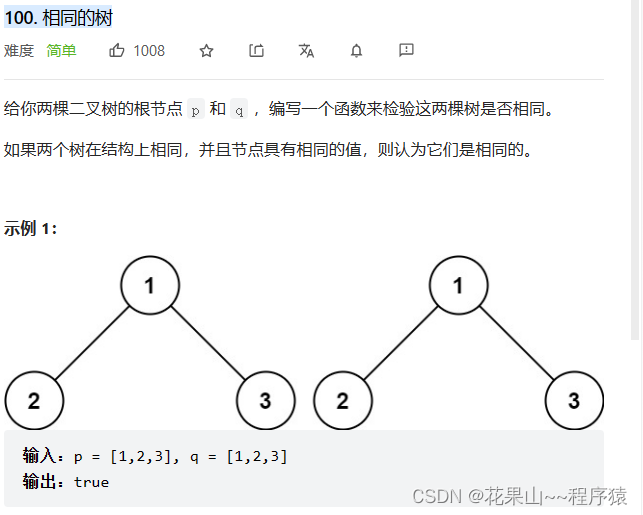
思路:两树同时遍历,如果不相同返回False;
代码如下:
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
if (p == NULL && q == NULL)
return true;
if(p == NULL || q == NULL)
return false;
if(p->val != q->val)
return false;
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
} 
3. 572. 另一棵树的子树
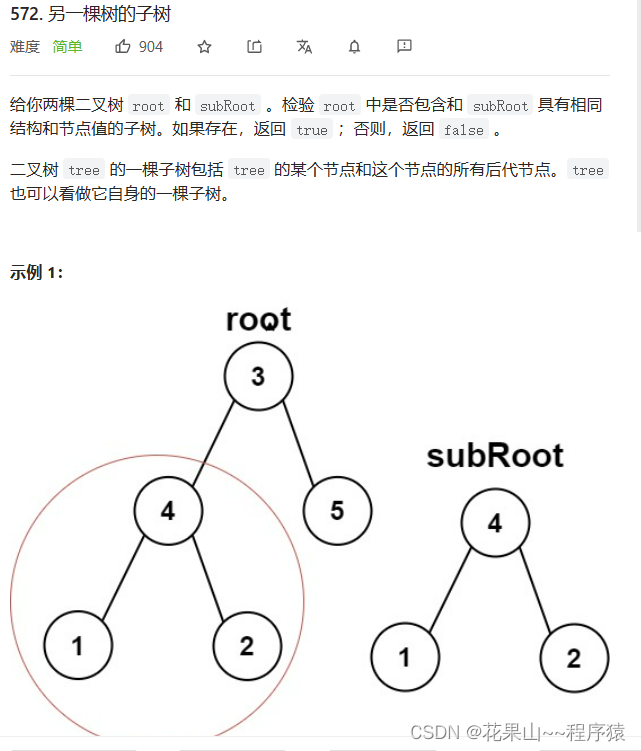
这个题是相同的树的一道变形题。
- 相同点:当根同subRoot树的根相同,则进入判断是否是相同的树这道题的逻辑。
- 不同点:是从一棵大树中寻找,中间可能存在多个目标子树,也可能没有,那么每一个根都可能是,所以需要遍历大树,一旦找到直接返回true,毕竟题目只要求存在。
代码如下:
bool isSymmetricSubTree(struct TreeNode* root1, struct TreeNode* root2)
{
// 第一种, 两树全为NULL
if(root1 == NULL && root2 == NULL)
return true;
// 第二种, 一树,为空,则不相等
if(root1 == NULL || root2 == NULL)
return false;
// 第三种, 数值不相等,则不相等。
if(root1->val != root2->val)
return false;
// 如果都不是则,这一组满足,判断下组,
return isSymmetricSubTree(root1->left, root2->left)
&& isSymmetricSubTree(root1->right, root2->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
if(root == NULL || subRoot == NULL)
return false;
if(isSymmetricSubTree(root, subRoot))
return true;
return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}
结语
本小节就到这里了,感谢小伙伴的浏览,如果有什么建议,欢迎在评论区评论,如果给小伙伴带来一些收获请留下你的小赞,你的点赞和关注将会成为博主创作的动力。