文章目录
- 1 RBF神经网络
- 1.1 简介
- 1.2 步骤
- 输入
- rbf层
- 核函数
- 中心点求解方法
- 输出
- 1.3 几个问题
- 2 分类
- 2.0 数据集
- 2.1 网络架构
- 2.2 代码
- 2.3 结果
- 3 回归
- 3.0 数据集
- 3.1 网络架构
- 3.2 代码
- 3.3 结果
- 4 代码(可直接食用)
众所周知,MATLAB工具箱里提供了RBF神经网络。个人认为这个东西虽然蛮好用的——有的时候比你自己写的效果都好。但是,不是长久之计。通过Pytorch能建立自定义程度更高的人工神经网络,往后在网络里面加乱七八糟的东西都很方便(比如GA/PSO求解超参之类的、比如微调模型架构之类的)。
看了眼网上的写法,用python实现的人还是挺多的,但是大多数还是选择用 numpy 实现 RBF,有用 torch 的,不是很多。
本文将首先简单介绍和推导RBF神经网络的理论,然后分别在分类数据集和回归数据集中演示该神经网络的具体搭建方法。
1 RBF神经网络
1.1 简介
径向基(Radial Basis Function, RBF)神经网络主要具有以下特性:
- 单隐层前馈神经网络。因此,RBF 神经网络一般都蛮简单的,毕竟只有一个隐藏层,也翻不出什么浪花。
- 隐藏层激活函数为径向基函数。这个也没有任何问题,这正式人家的特点。
- 最终结果是隐藏层结果的线性组合。
因为径向基函数图像基本上都呈现为钟形,所以径向基神经网络可以简单地理解为由多个钟形函数加权求和凑出来的一个拟合线。
因为 RBF 在隐藏层用了个核函数把数据从低维空间映射到高维空间以求解线性不可分问题,又在输出时用一个简单的线性关系计算 RBF 层的结果,所以我们可以这样理解:
RBF 神经网络 输入 ——> 输出 是一段非线性关系。
RBF 神经网络 隐层 ——> 输出 是一段线性关系。
1.2 步骤
步骤分为三步(输入,rbf层,输出):
输入
输入没啥好说的,就跟正常神经网络一样,有几个特征就用几个输入神经元。
rbf层
这部分相当于借鉴了聚类算法的思路,根据数据的特性把输入数据拆分为了 n(隐藏层神经元个数) 类,再由每个神经元负责自己的范围内的数据(主要是由激活函数的数学性质导致的)。
因此这就涉及到了每个神经元负责的范围大小,称为中心宽度;也涉及到了类别的数量确定,也就是隐藏层神经元的数量。
因为每个神经元只负责自己范围内的那些数据,在逼近最优值的时候不需要管其他神经元内的数据,因此这是一个局部逼近网络。
rbf层蛮有讲究的。大概有这几个点比较重要。
核函数
核函数就是一个能把低维数据映射到高维的东西,拿高斯核函数举例:
φ ( x i , r j ) = e − ∣ ∣ x i − c j ∣ ∣ 2 2 σ 2 \varphi(x_i,r_j)=e^{-\frac{||x_i-c_j||^2}{2\sigma^2}} φ(xi,rj)=e−2σ2∣∣xi−cj∣∣2
其中, ∣ ∣ x i − c j ∣ ∣ ||x_i-c_j|| ∣∣xi−cj∣∣是指点 x i x_i xi与中心点 c j c_j cj的欧氏距离, σ \sigma σ是指高斯核的宽度。
这个公式实际上就是:
φ ′ ( x i → , r j → ) = e − x i → ∙ r j → σ 2 \varphi'(\overrightarrow{x_i},\overrightarrow{r_j})=e^{-\frac{\overrightarrow{x_i}\bullet \overrightarrow{r_j}}{\sigma^2}} φ′(xi,rj)=e−σ2xi∙rj
这就好办了,幂级数展开
φ ′ ( x i → , r j → ) = ∑ n = 0 + ∞ ( x i → ∙ r j → ) n σ n n ! \varphi'(\overrightarrow{x_i},\overrightarrow{r_j})=\sum_{n=0}^{+\infty}{\frac{(\overrightarrow{x_i}\bullet \overrightarrow{r_j})^n}{\sigma^n\ n!}} φ′(xi,rj)=n=0∑+∞σn n!(xi∙rj)n
因为 n 趋近于无穷,所以这一对乘起来之后维度数据就上去了。
当然除了高斯核函数,还有很多核函数,比如
反常S型函数: φ ( r ) = 1 1 + e ∣ ∣ x i − c j ∣ ∣ 2 2 σ 2 \varphi(r)=\frac{1}{1+e^{\frac{||x_i-c_j||^2}{2\sigma^2}}} φ(r)=1+e2σ2∣∣xi−cj∣∣21
拟多二次函数: φ ( r ) = 1 ∣ ∣ x i − c j ∣ ∣ 2 + σ 2 \varphi(r)=\frac{1}{\sqrt{||x_i-c_j||^2+\sigma^2}} φ(r)=∣∣xi−cj∣∣2+σ21
等等
中心点求解方法
- 随机方法(直接计算法)
隐含层神经元的中心是随机地在输入样本中选取,且中心固定。一旦中心固定下来,隐含层神经元的输出便是已知的,这样的神经网络的连接权就可以通过求解线性方程组来确定。适用于样本数据的分布具有明显代表性。
- 无监督学习方法
思路像聚类
第一步:无监督学习过程,求解隐含层基函数的中心与方差
第二步:有监督学习过程,求解隐含层到输出层之间的权值
首先,选取h个中心做k-means聚类,对于高斯核函数的径向基,方差由公式求解:
σ i = c m a x 2 h i = 1 , 2 , 3 , … , h \sigma_i=\frac{c_{max}}{2h} \ \ \ i=1,2,3, …, h σi=2hcmax i=1,2,3,…,h
c m a x c_{max} cmax为所选取中心点之间的最大距离。
隐含层至输出层之间的神经元的连接权值可以用最小二乘法直接计算得到,即对损失函数求解关于w的偏导数,使其等于0,可以化简得到计算公式为:
w = e x p ( h c m a x 2 ∣ ∣ x p − c i ∣ ∣ 2 ) p = 1 , 2 , 3 , … , P ; i = 1 , 2 , 3 , … , h w = exp(\frac{h}{c^2_{max}}||x_p-c_i||^2) \ \ \ p=1,2,3, …, P;\ i = 1,2,3, …, h w=exp(cmax2h∣∣xp−ci∣∣2) p=1,2,3,…,P; i=1,2,3,…,h
- 有监督学习方法
通过训练样本集来获得满足监督要求的网络中心和其他权重参数,经历一个误差修正学习的过程,与BP网络的学习原理一样,同样采用梯度下降法。因此RBF同样可以被当作BP神经网络的一种。
这样,概括的来说RBF神经网络的隐层将输入空间映射到一个新空间 ,输出层在该新空间中实现线性组合器 ,可调节参数就是该线性组合器的权 。
这部分感觉这篇讲的更好一点。
输出
输出也没什么可以称道的,类似于简单的线性回归吧。实际上就是对上一层的聚类的结果的一个线性拟合(类似线性加权求和)。
1.3 几个问题
-
同样都是用核函数解决问题,在解决线性不可分问题时的 SVM 和 RBF 有什么区别吗?
看到高斯核,感觉大家第一想法应该都是SVM吧,这俩同样都是计算距离,两者计算的距离还是有点区别的:
SVM:计算与其他输入点间的距离,而且中心点是在已存在的样本中选取出来的。
RBF神经网络:计算的是输入点和几个神经元节点中心的距离,思路有点像聚类。 -
为什么用 RBF 而不用 BP?RBF 的优势在哪里?
- 快:相比于BP,RBF神经网络用了非线性技术做了优化,减小了计算量,增快了学习速率;而BP必须要用某种非线性优化技术,这大大损耗了时间。
- 局部逼近:(这个不知道算不算优点)RBF神经网络用的是局部逼近,所以空间中只有少数几个连接的权重会影响到网络的输出;但是BP就不一样,它的参数牵一发而动全身,稍微改一个参数就会导致整个结果大变。
-
RBF 和 BP 架构的区别?
- RBF是单层的,BP多少层理论上都可以。
- RBF局部逼近,BP全局逼近。
- RBF收敛的相对快一点。
2 分类
2.0 数据集
数据集我采用的是之前接手的一个保险理赔项目。
目标是判断用户是不是来骗保的,给了一大堆特征,这里我就不详细解释是哪些特征了,这篇文章主要负责搭建模型。
归一化之后发现数据还是非常稀疏的,而且看着可能二值化效果会不错,嫌麻烦,不尝试了,就直接拿这个用也没什么大问题。
是一个4分类任务,结果可能没2分类好看,这跟项目的数据也有关,本身数据也比较脏、噪声也比较多,感觉特征与 label 之间的联系也不是特别紧密。不过问题不大,我们的重心还是放在搭网络上。
数据集缺点还包括样本不平衡,确实会影响结果。
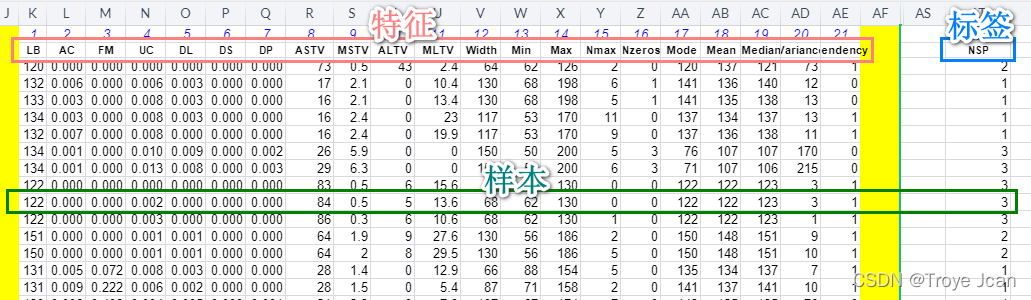
data.csv (36221x24)=> 已经包括 label 了
2.1 网络架构
torch 输出的架构如下

架构很简单,这个确实没办法,毕竟 RBF 神经网络就是单层的……
一共是1层隐藏层(32个神经元)。
也尝试过 64 个神经元和一些其他的参数,效果反而没这个好。
2.2 代码
分类任务的相关文件如下

RBF_clf.py 分类模型架构
data.csv 分类数据集
run.py 主函数
utils.py 相关函数和类
run.py
import os
import numpy
import torch
import random
from utils import Config, CLF_Model, REG_Model
from clf_model.RBF_clf import RBF
seed = 1129
random.seed(seed)
numpy.random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
os.environ['PYTHONHASHSEED'] = str(seed)
# 分类
if __name__ == '__main__':
config = Config(
data_path="dataset_clf/data.csv",
name="RBF",
batch_size=128,
learning_rate=0.007,
epoch=10
)
clf = RBF(
input_n=len(config.input_col),
output_n=len(config.output_class),
hidden_size=32
)
print(clf)
model = CLF_Model(clf, config)
model.run()
RBF_clf.py
import sys
import torch
from torch.nn import Linear, ReLU, ModuleList, Sequential, Dropout, Softmax, Tanh
import torch.nn as nn
class RBF(torch.nn.Module):
# 默认三层隐藏层,分别有128个 64个 16个神经元
def __init__(self, input_n, output_n, hidden_size=10, kernel="gaussian"):
"""
:param input_n: int 输入神经元个数
:param output_n: int 输出神经元个数
:param hidden_size: int 隐藏层神经元个数
:param kernel: string 核函数
"""
super(RBF, self).__init__()
self.input_n = input_n
self.output_n = output_n
# 输入层 -> RBF层
self.input_layer = rbf_layer(input_n, hidden_size, kernel)
# RBF层 -> 输出层
self.output_layer = nn.Linear(hidden_size, output_n)
def forward(self, x):
rbf_ret = self.input_layer(x)
output = self.output_layer(rbf_ret)
return output
class rbf_layer(torch.nn.Module):
def __init__(self, input_n, hidden_size=10, kernel="gaussian"):
"""
:param input_n: int 输入神经元个数
:param hidden_size: int 隐藏层神经元个数
:param kernel: string 核函数
"""
super(rbf_layer, self).__init__()
self.input_n = input_n
self.hidden_size = hidden_size
self.kernel = kernel
kernel_existed = {
'gaussian': gaussian,
'linear': linear,
'quadratic': quadratic,
'inverse quadratic': inverse_quadratic,
'multiquadric': multiquadric,
'inverse multiquadric': inverse_multiquadric,
'spline': spline,
'poisson one': poisson_one,
'poisson two': poisson_two,
'matern32': matern32,
'matern52': matern52
}
if self.kernel not in kernel_existed:
print("Unknown kernel function, plz check and modify RBF.kernel")
sys.exit(0)
self.centres = nn.Parameter(torch.Tensor(hidden_size, input_n))
self.log_sigmas = nn.Parameter(torch.Tensor(hidden_size))
# 初始化各项参数(聚类中心)
self.ini_parameters()
def ini_parameters(self):
nn.init.normal_(self.centres, 0, 1)
nn.init.constant_(self.log_sigmas, 0)
def forward(self, x):
# x: [batch_size, input_n]
size = (x.size(0), self.hidden_size, self.input_n)
# 调整数据shape
# point: [batch_size, hidden_size, input_n]
# center: [batch_size, hidden_size, input_n]
point = x.unsqueeze(1).expand(size)
centers = self.centres.unsqueeze(0).expand(size)
distance_p_c = self.distance(point, centers)
return distance_p_c
def distance(self, x1, x2):
distances = (x1 - x2).pow(2).sum(-1).pow(0.5) / torch.exp(self.log_sigmas).unsqueeze(0)
return distances
# 可能会用到的几个RBF核函数
def gaussian(alpha):
phi = torch.exp(-1*alpha.pow(2))
return phi
def linear(alpha):
phi = alpha
return phi
def quadratic(alpha):
phi = alpha.pow(2)
return phi
def inverse_quadratic(alpha):
phi = torch.ones_like(alpha) / (torch.ones_like(alpha) + alpha.pow(2))
return phi
def multiquadric(alpha):
phi = (torch.ones_like(alpha) + alpha.pow(2)).pow(0.5)
return phi
def inverse_multiquadric(alpha):
phi = torch.ones_like(alpha) / (torch.ones_like(alpha) + alpha.pow(2)).pow(0.5)
return phi
def spline(alpha):
phi = (alpha.pow(2) * torch.log(alpha + torch.ones_like(alpha)))
return phi
def poisson_one(alpha):
phi = (alpha - torch.ones_like(alpha)) * torch.exp(-alpha)
return phi
def poisson_two(alpha):
phi = ((alpha - 2*torch.ones_like(alpha)) / 2*torch.ones_like(alpha)) * alpha * torch.exp(-alpha)
return phi
def matern32(alpha):
phi = (torch.ones_like(alpha) + 3**0.5*alpha)*torch.exp(-3**0.5*alpha)
return phi
def matern52(alpha):
phi = (torch.ones_like(alpha) + 5**0.5*alpha + (5/3) * alpha.pow(2))*torch.exp(-5**0.5*alpha)
return phi
util.py
import sys
import numpy as np
import pandas as pd
import torch
import torch.nn.functional as F
from matplotlib import pyplot as plt
from sklearn import metrics
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
import time
from datetime import timedelta
# 一个数据格式。感觉这玩意好多余啊,但是nlp写多了就很习惯的写了一个上去 => 主要是不写没法封装
class Dataset(torch.utils.data.Dataset):
def __init__(self, data_df):
self.label = torch.from_numpy(data_df['label'].values)
self.data = torch.from_numpy(data_df[data_df.columns[:-1]].values).to(torch.float32)
# 每次迭代取出对应的data和author
def __getitem__(self, idx):
batch_data = self.get_batch_data(idx)
batch_label = self.get_batch_label(idx)
return batch_data, batch_label
# 下面的几条没啥用其实,就是为__getitem__服务的
def classes(self):
return self.label
def __len__(self):
return self.data.size(0)
def get_batch_label(self, idx):
return np.array(self.label[idx])
def get_batch_data(self, idx):
return self.data[idx]
# 存数据,加载数据用的
class Config:
def __init__(self, data_path, name, batch_size, learning_rate, epoch):
"""
:param data_path: string 数据文件路径
:param name: string 模型名字
:param batch_size: int 多少条数据组成一个batch
:param learning_rate: float 学习率
:param epoch: int 学几轮
"""
self.name = name
self.data_path = data_path
self.batch_size = batch_size
self.learning_rate = learning_rate
self.epoch = epoch
self.train_loader, self.dev_loader, self.test_loader = self.load_tdt()
self.input_col, self.output_class = self.get_class()
# 加载train, dev, test,把数据封装成Dataloader类
def load_tdt(self):
file = self.read_file()
train_dev_test = self.cut_data(file)
tdt_loader = [self.load_data(i) for i in train_dev_test]
return tdt_loader[0], tdt_loader[1], tdt_loader[2]
# 读文件
def read_file(self):
file = pd.read_csv(self.data_path, encoding="utf-8-sig", index_col=None)
# 保险起见,确认最后一列列名为label
file.columns.values[-1] = "label"
self.if_nan(file)
return file
# 切7:1:2 => 训练:验证:测试
def cut_data(self, data_df):
try:
train_df, test_dev_df = train_test_split(data_df, test_size=0.3, random_state=1129, stratify=data_df["label"])
dev_df, test_df = train_test_split(test_dev_df, test_size=0.66, random_state=1129, stratify=test_dev_df["label"])
except ValueError:
train_df, test_dev_df = train_test_split(data_df, test_size=0.3, random_state=1129)
dev_df, test_df = train_test_split(test_dev_df, test_size=0.66, random_state=1129)
return [train_df, dev_df, test_df]
# Dataloader 封装进去
def load_data(self, data_df):
dataset = Dataset(data_df)
return torch.utils.data.DataLoader(dataset, batch_size=self.batch_size)
# 检验输入输出是否有空值
def if_nan(self, data):
if data.isnull().any().any():
empty = data.isnull().any()
print(empty[empty].index)
print("Empty data exists")
sys.exit(0)
# 后面输出混淆矩阵用的
def get_class(self):
file = self.read_file()
label = file[file.columns[-1]]
label = list(set(list(label)))
return file.columns[:-1], label
# 跑clf用的,里面包含了训练,测试,评价等等的代码
class CLF_Model:
def __init__(self, model, config):
self.model = model
self.config = config
def run(self):
self.train(self.model)
def train(self, model):
dev_best_loss = float('inf')
start_time = time.time()
# 模型为训练模式
model.train()
# 定义优化器
optimizer = torch.optim.Adam(model.parameters(), lr=self.config.learning_rate)
# 记录训练、验证的准确率和损失
acc_list = [[], []]
loss_list = [[], []]
# 记录损失不下降的epoch数,到达20之后就直接退出 => 训练无效,再训练下去可能过拟合
break_epoch = 0
for epoch in range(self.config.epoch):
print('Epoch [{}/{}]'.format(epoch + 1, self.config.epoch))
for index, (trains, labels) in enumerate(self.config.train_loader):
# 归零
model.zero_grad()
# 得到预测结果,是一堆概率
outputs = model(trains)
# 交叉熵计算要long的类型
labels = labels.long()
# 计算交叉熵损失
loss = F.cross_entropy(outputs, labels)
# 反向传播loss
loss.backward()
# 优化参数
optimizer.step()
# 每100个迭代或者跑完一个epoch后,验证一下
if (index % 100 == 0 and index != 0) or index == len(self.config.train_loader) - 1:
true = labels.data.cpu()
# 预测类别
predict = torch.max(outputs.data, 1)[1].cpu()
# 计算训练准确率
train_acc = metrics.accuracy_score(true, predict)
# 计算验证准确率和loss
dev_acc, dev_loss = self.evaluate(model)
# 查看验证loss是不是进步了
if dev_loss < dev_best_loss:
dev_best_loss = dev_loss
improve = '*'
break_epoch = 0
else:
improve = ''
break_epoch += 1
time_dif = self.get_time_dif(start_time)
# 输出阶段性结果
msg = 'Iter: {0:>6}, Train Loss: {1:>5.3}, Train Acc: {2:>6.3%}, Val Loss: {3:>5.3}, Val Acc: {4:>6.3%}, Time: {5} {6}'
print(msg.format(index, loss.item(), train_acc, dev_loss, dev_acc, time_dif, improve))
# 为了画图准备的,记录每个epoch的结果
if index == len(self.config.train_loader) - 1:
acc_list[0].append(train_acc)
acc_list[1].append(dev_acc)
loss_list[0].append(loss.item())
loss_list[1].append(dev_loss)
# 验证集评估时模型编程验证模式了,现在变回训练模式
model.train()
# 20个epoch损失不变,直接退出训练
if break_epoch > 20:
self.config.epoch = epoch+1
break
# 测试
self.test(model)
# 画图
self.draw_curve(acc_list, loss_list, self.config.epoch)
def test(self, model):
start_time = time.time()
# 测试准确率,测试损失,测试分类报告,测试混淆矩阵
test_acc, test_loss, test_report, test_confusion = self.evaluate(model, test=True)
msg = 'Test Loss: {0:>5.3}, Test Acc: {1:>6.3%}'
print(msg.format(test_loss, test_acc))
print("Precision, Recall and F1-Score...")
print(test_report)
print("Confusion Matrix...")
print(test_confusion)
time_dif = self.get_time_dif(start_time)
print("Time usage:", time_dif)
def evaluate(self, model, test=False):
# 模型模式变一下
model.eval()
loss_total = 0
predict_all = np.array([], dtype=int)
labels_all = np.array([], dtype=int)
# 如果是测试模式(这一段写的不是很好)
if test:
with torch.no_grad():
for (dev, labels) in self.config.test_loader:
outputs = model(dev)
labels = labels.long()
loss = F.cross_entropy(outputs, labels)
loss_total += loss
labels = labels.data.cpu().numpy()
predict = torch.max(outputs.data, 1)[1].cpu().numpy()
labels_all = np.append(labels_all, labels)
predict_all = np.append(predict_all, predict)
acc = metrics.accuracy_score(labels_all, predict_all)
report = metrics.classification_report(labels_all, predict_all, target_names=[str(i) for i in self.config.get_class()[1]], digits=4)
confusion = metrics.confusion_matrix(labels_all, predict_all)
return acc, loss_total / len(self.config.dev_loader), report, confusion
# 不是测试模式
with torch.no_grad():
for (dev, labels) in self.config.dev_loader:
outputs = model(dev)
labels = labels.long()
loss = F.cross_entropy(outputs, labels)
loss_total += loss
labels = labels.data.cpu().numpy()
predict = torch.max(outputs.data, 1)[1].cpu().numpy()
labels_all = np.append(labels_all, labels)
predict_all = np.append(predict_all, predict)
acc = metrics.accuracy_score(labels_all, predict_all)
return acc, loss_total / len(self.config.dev_loader)
# 算时间损耗
def get_time_dif(self, start_time):
end_time = time.time()
time_dif = end_time - start_time
return timedelta(seconds=int(round(time_dif)))
# 画图
def draw_curve(self, acc_list, loss_list, epochs):
x = range(0, epochs)
y1 = loss_list[0]
y2 = loss_list[1]
y3 = acc_list[0]
y4 = acc_list[1]
plt.figure(figsize=(13, 13))
plt.subplot(2, 1, 1)
plt.plot(x, y1, color="blue", label="train_loss", linewidth=2)
plt.plot(x, y2, color="orange", label="val_loss", linewidth=2)
plt.title("Loss_curve", fontsize=20)
plt.xlabel(xlabel="Epochs", fontsize=15)
plt.ylabel(ylabel="Loss", fontsize=15)
plt.legend()
plt.subplot(2, 1, 2)
plt.plot(x, y3, color="blue", label="train_acc", linewidth=2)
plt.plot(x, y4, color="orange", label="val_acc", linewidth=2)
plt.title("Acc_curve", fontsize=20)
plt.xlabel(xlabel="Epochs", fontsize=15)
plt.ylabel(ylabel="Accuracy", fontsize=15)
plt.legend()
plt.savefig("images/"+self.config.name+"_Loss&acc.png")
2.3 结果
训练ing……

效果还不错。在 MLP 中,神经网络很容易陷入局部最优导致准确率一直卡在76%,但是在 RBF 里面神经网络在第三个epoch就跳出来了,这可能跟它追求局部收敛有关。
第三类的精确率感人,不过其他分类效果挺好的。感觉是数据集的问题,对比之前 MLP 的结果可以说是又快又好了。
虽然没有彻底解决第三类分类不准确的问题,但是在第二类上的精确度确实有所提升,而且收敛的很快。

曲线如下(看曲线感觉可以适当增加下epoch,虽然 loss 确实趋于平稳了,但是怎么感觉还能跌)

3 回归
3.0 数据集
用的2023美赛春季赛Y题数据,在原有的数据集上加了很多船的参数,再把两个 dataset 合一起。
预处理的操作简单暴力,重复值的行删掉,部分含空值多的行删掉,方便填充的随机森林下,不方便填充的直接暴力填0。
平时肯定是不能这么干的,但是这里我们只是需要一个数据集而已,重点还是模型。
data.csv(2793x39)=> 已经包括 label 了
label.csv(2793x1)
3.1 网络架构
torch 输出的架构如下

跟分类同理
架构很简单,这个确实没办法,毕竟 RBF 神经网络就是单层的……
一共是1层隐藏层(32个神经元)。
也尝试过多的少的神经元数量和一些其他的参数,都被打爆了。
3.2 代码
回归任务的相关文件如下

data.csv 回归数据集
RBF_reg.py 回归模型架构
run.py 主函数
utils.py 相关函数和类
run.py
import os
import numpy
import torch
import random
from utils import Config, CLF_Model, REG_Model
from clf_model.RBF_clf import RBF
seed = 1129
random.seed(seed)
numpy.random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
os.environ['PYTHONHASHSEED'] = str(seed)
from reg_model.RBF_reg import RBF
# 回归
if __name__ == '__main__':
config = Config(
data_path="dataset_reg/data.csv",
name="RBF",
batch_size=16,
learning_rate=0.01,
epoch=200
)
# 看是几输出问题
reg = RBF(
input_n=len(config.input_col),
output_n=1,
hidden_size=32,
)
print(reg)
model = REG_Model(reg, config)
model.run()
utils.py
import sys
import numpy as np
import pandas as pd
import torch
import torch.nn.functional as F
from matplotlib import pyplot as plt
from sklearn import metrics
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
import time
from datetime import timedelta
# 一个数据格式。感觉这玩意好多余啊,但是nlp写多了就很习惯的写了一个上去 => 主要是不写没法封装
class Dataset(torch.utils.data.Dataset):
def __init__(self, data_df):
self.label = torch.from_numpy(data_df['label'].values)
self.data = torch.from_numpy(data_df[data_df.columns[:-1]].values).to(torch.float32)
# 每次迭代取出对应的data和author
def __getitem__(self, idx):
batch_data = self.get_batch_data(idx)
batch_label = self.get_batch_label(idx)
return batch_data, batch_label
# 下面的几条没啥用其实,就是为__getitem__服务的
def classes(self):
return self.label
def __len__(self):
return self.data.size(0)
def get_batch_label(self, idx):
return np.array(self.label[idx])
def get_batch_data(self, idx):
return self.data[idx]
# 存数据,加载数据用的
class Config:
def __init__(self, data_path, name, batch_size, learning_rate, epoch):
"""
:param data_path: string 数据文件路径
:param name: string 模型名字
:param batch_size: int 多少条数据组成一个batch
:param learning_rate: float 学习率
:param epoch: int 学几轮
"""
self.name = name
self.data_path = data_path
self.batch_size = batch_size
self.learning_rate = learning_rate
self.epoch = epoch
self.train_loader, self.dev_loader, self.test_loader = self.load_tdt()
self.input_col, self.output_class = self.get_class()
# 加载train, dev, test,把数据封装成Dataloader类
def load_tdt(self):
file = self.read_file()
train_dev_test = self.cut_data(file)
tdt_loader = [self.load_data(i) for i in train_dev_test]
return tdt_loader[0], tdt_loader[1], tdt_loader[2]
# 读文件
def read_file(self):
file = pd.read_csv(self.data_path, encoding="utf-8-sig", index_col=None)
# 保险起见,确认最后一列列名为label
file.columns.values[-1] = "label"
self.if_nan(file)
return file
# 切7:1:2 => 训练:验证:测试
def cut_data(self, data_df):
try:
train_df, test_dev_df = train_test_split(data_df, test_size=0.3, random_state=1129, stratify=data_df["label"])
dev_df, test_df = train_test_split(test_dev_df, test_size=0.66, random_state=1129, stratify=test_dev_df["label"])
except ValueError:
train_df, test_dev_df = train_test_split(data_df, test_size=0.3, random_state=1129)
dev_df, test_df = train_test_split(test_dev_df, test_size=0.66, random_state=1129)
return [train_df, dev_df, test_df]
# Dataloader 封装进去
def load_data(self, data_df):
dataset = Dataset(data_df)
return torch.utils.data.DataLoader(dataset, batch_size=self.batch_size)
# 检验输入输出是否有空值
def if_nan(self, data):
if data.isnull().any().any():
empty = data.isnull().any()
print(empty[empty].index)
print("Empty data exists")
sys.exit(0)
# 后面输出混淆矩阵用的
def get_class(self):
file = self.read_file()
label = file[file.columns[-1]]
label = list(set(list(label)))
return file.columns[:-1], label
# 跑reg用的,里面包含了训练,测试,评价等等的代码
class REG_Model:
def __init__(self, model, config):
self.model = model
self.config = config
def run(self):
self.train(self.model)
def train(self, model):
dev_best_loss = float('inf')
start_time = time.time()
# 模型为训练模式
model.train()
# 定义优化器
optimizer = torch.optim.Adam(model.parameters(), lr=self.config.learning_rate)
acc_list = [[], []]
loss_list = [[], []]
# 记录损失不下降的epoch数,到达20之后就直接退出 => 训练无效,再训练下去可能过拟合
break_epoch = 0
for epoch in range(self.config.epoch):
print('Epoch [{}/{}]'.format(epoch + 1, self.config.epoch))
for index, (trains, labels) in enumerate(self.config.train_loader):
# 归零
model.zero_grad()
# 得到预测结果
outputs = model(trains)
# MSE计算要float的类型
labels = labels.to(torch.float)
# 计算MSE损失
loss = torch.nn.MSELoss()(outputs, labels)
# 反向传播loss
loss.backward()
# 优化参数
optimizer.step()
# 每100个迭代或者跑完一个epoch后,验证一下
if (index % 100 == 0 and index != 0) or index == len(self.config.train_loader) - 1:
true = labels.data.cpu()
# 预测数据
predict = outputs.data.cpu()
# 计算训练准确度 R2
train_acc = r2_score(true, predict)
# 计算验证准确度 R2 和 loss
dev_acc, dev_loss, dev_mse = self.evaluate(model)
# 查看验证loss是不是进步了
if dev_loss < dev_best_loss:
dev_best_loss = dev_loss
improve = '*'
break_epoch = 0
else:
improve = ''
break_epoch += 1
time_dif = self.get_time_dif(start_time)
# 输出阶段性结果
msg = 'Iter: {0:>6}, Train Loss: {1:>5.3}, Train R2: {2:>6.3}, Val Loss: {3:>5.3}, Val R2: {4:>6.3}, Val Mse: {5:>6.3}, Time: {6} {7}'
print(msg.format(index, loss.item(), train_acc, dev_loss, dev_acc, dev_mse, time_dif, improve))
# 为了画图准备的,记录每个epoch的结果
if index == len(self.config.train_loader) - 1:
acc_list[0].append(train_acc)
acc_list[1].append(dev_acc)
loss_list[0].append(loss.item())
loss_list[1].append(dev_loss)
# 验证集评估时模型编程验证模式了,现在变回训练模式
model.train()
# 20个epoch损失不变,直接退出训练
if break_epoch > 20:
self.config.epoch = epoch+1
break
# 测试
self.test(model)
# 画图
self.draw_curve(acc_list, loss_list, self.config.epoch)
def test(self, model):
start_time = time.time()
# 测试准确度 R2,测试损失,测试MSE
test_acc, test_loss, mse = self.evaluate(model, test=True)
msg = 'Test R2: {0:>5.3}, Test loss: {1:>6.3}, Test MSE: {2:>6.3}'
print(msg.format(test_acc, test_loss, mse))
time_dif = self.get_time_dif(start_time)
print("Time usage:", time_dif)
def evaluate(self, model, test=False):
# 模型模式变一下
model.eval()
loss_total = 0
predict_all = np.array([], dtype=int)
labels_all = np.array([], dtype=int)
# 如果是测试模式(这一段写的不是很好)
if test:
with torch.no_grad():
for (dev, labels) in self.config.test_loader:
outputs = model(dev)
labels = labels.to(torch.float)
loss = torch.nn.MSELoss()(outputs, labels)
loss_total += loss
labels = labels.data.cpu().numpy()
predict = outputs.data.cpu().numpy()
labels_all = np.append(labels_all, labels)
predict_all = np.append(predict_all, predict)
# 不是测试模式
else:
with torch.no_grad():
for (dev, labels) in self.config.dev_loader:
outputs = model(dev)
labels = labels.long()
loss = torch.nn.MSELoss()(outputs, labels)
loss_total += loss
labels = labels.data.cpu().numpy()
predict = outputs.data.cpu().numpy()
labels_all = np.append(labels_all, labels)
predict_all = np.append(predict_all, predict)
r2 = r2_score(labels_all, predict_all)
mse = mean_squared_error(labels_all, predict_all)
if test:
return r2, loss_total / len(self.config.test_loader), mse
else:
return r2, loss_total / len(self.config.dev_loader), mse
# 算时间损耗
def get_time_dif(self, start_time):
end_time = time.time()
time_dif = end_time - start_time
return timedelta(seconds=int(round(time_dif)))
# 画图
def draw_curve(self, acc_list, loss_list, epochs):
x = range(0, epochs)
y1 = loss_list[0]
y2 = loss_list[1]
y3 = acc_list[0]
y4 = acc_list[1]
plt.figure(figsize=(13, 13))
plt.subplot(2, 1, 1)
plt.plot(x, y1, color="blue", label="train_loss", linewidth=2)
plt.plot(x, y2, color="orange", label="val_loss", linewidth=2)
plt.title("Loss_curve", fontsize=20)
plt.xlabel(xlabel="Epochs", fontsize=15)
plt.ylabel(ylabel="Loss", fontsize=15)
plt.legend()
plt.subplot(2, 1, 2)
plt.plot(x, y3, color="blue", label="train_acc", linewidth=2)
plt.plot(x, y4, color="orange", label="val_acc", linewidth=2)
plt.title("Acc_curve", fontsize=20)
plt.xlabel(xlabel="Epochs", fontsize=15)
plt.ylabel(ylabel="Accuracy", fontsize=15)
plt.legend()
plt.savefig("images/"+self.config.name+"_Loss&acc.png")
RBF_reg.py
import sys
import torch
from torch.nn import Linear, ReLU, ModuleList, Sequential, Dropout, Softmax, Tanh
import torch.nn as nn
class RBF(torch.nn.Module):
# 默认三层隐藏层,分别有128个 64个 16个神经元
def __init__(self, input_n, output_n, hidden_size=10, kernel="gaussian"):
"""
:param input_n: int 输入神经元个数
:param output_n: int 输出神经元个数
:param hidden_size: int 隐藏层神经元个数
:param kernel: string 核函数
"""
super(RBF, self).__init__()
self.input_n = input_n
self.output_n = output_n
# 输入层 -> RBF层
self.input_layer = rbf_layer(input_n, hidden_size, kernel)
# RBF层 -> 输出层
self.output_layer = nn.Linear(hidden_size, output_n)
def forward(self, x):
rbf_ret = self.input_layer(x)
output = self.output_layer(rbf_ret)
# 减少多余的一维,方便计算mse,不然warning
output = output.squeeze(1)
return output
class rbf_layer(torch.nn.Module):
def __init__(self, input_n, hidden_size=10, kernel="gaussian"):
"""
:param input_n: int 输入神经元个数
:param hidden_size: int 隐藏层神经元个数
:param kernel: string 核函数
"""
super(rbf_layer, self).__init__()
self.input_n = input_n
self.hidden_size = hidden_size
self.kernel = kernel
kernel_existed = {
'gaussian': gaussian,
'linear': linear,
'quadratic': quadratic,
'inverse quadratic': inverse_quadratic,
'multiquadric': multiquadric,
'inverse multiquadric': inverse_multiquadric,
'spline': spline,
'poisson one': poisson_one,
'poisson two': poisson_two,
'matern32': matern32,
'matern52': matern52
}
if self.kernel not in kernel_existed:
print("Unknown kernel function, plz check and modify RBF.kernel")
sys.exit(0)
self.centres = nn.Parameter(torch.Tensor(hidden_size, input_n))
self.log_sigmas = nn.Parameter(torch.Tensor(hidden_size))
# 初始化各项参数(聚类中心)
self.ini_parameters()
def ini_parameters(self):
nn.init.normal_(self.centres, 0, 1)
nn.init.constant_(self.log_sigmas, 0)
def forward(self, x):
# x: [batch_size, input_n]
size = (x.size(0), self.hidden_size, self.input_n)
# 调整数据shape
# point: [batch_size, hidden_size, input_n]
# center: [batch_size, hidden_size, input_n]
point = x.unsqueeze(1).expand(size)
centers = self.centres.unsqueeze(0).expand(size)
distance_p_c = self.distance(point, centers)
return distance_p_c
def distance(self, x1, x2):
distances = (x1 - x2).pow(2).sum(-1).pow(0.5) / torch.exp(self.log_sigmas).unsqueeze(0)
return distances
# 可能会用到的几个RBF核函数
def gaussian(alpha):
phi = torch.exp(-1*alpha.pow(2))
return phi
def linear(alpha):
phi = alpha
return phi
def quadratic(alpha):
phi = alpha.pow(2)
return phi
def inverse_quadratic(alpha):
phi = torch.ones_like(alpha) / (torch.ones_like(alpha) + alpha.pow(2))
return phi
def multiquadric(alpha):
phi = (torch.ones_like(alpha) + alpha.pow(2)).pow(0.5)
return phi
def inverse_multiquadric(alpha):
phi = torch.ones_like(alpha) / (torch.ones_like(alpha) + alpha.pow(2)).pow(0.5)
return phi
def spline(alpha):
phi = (alpha.pow(2) * torch.log(alpha + torch.ones_like(alpha)))
return phi
def poisson_one(alpha):
phi = (alpha - torch.ones_like(alpha)) * torch.exp(-alpha)
return phi
def poisson_two(alpha):
phi = ((alpha - 2*torch.ones_like(alpha)) / 2*torch.ones_like(alpha)) * alpha * torch.exp(-alpha)
return phi
def matern32(alpha):
phi = (torch.ones_like(alpha) + 3**0.5*alpha)*torch.exp(-3**0.5*alpha)
return phi
def matern52(alpha):
phi = (torch.ones_like(alpha) + 5**0.5*alpha + (5/3) * alpha.pow(2))*torch.exp(-5**0.5*alpha)
return phi
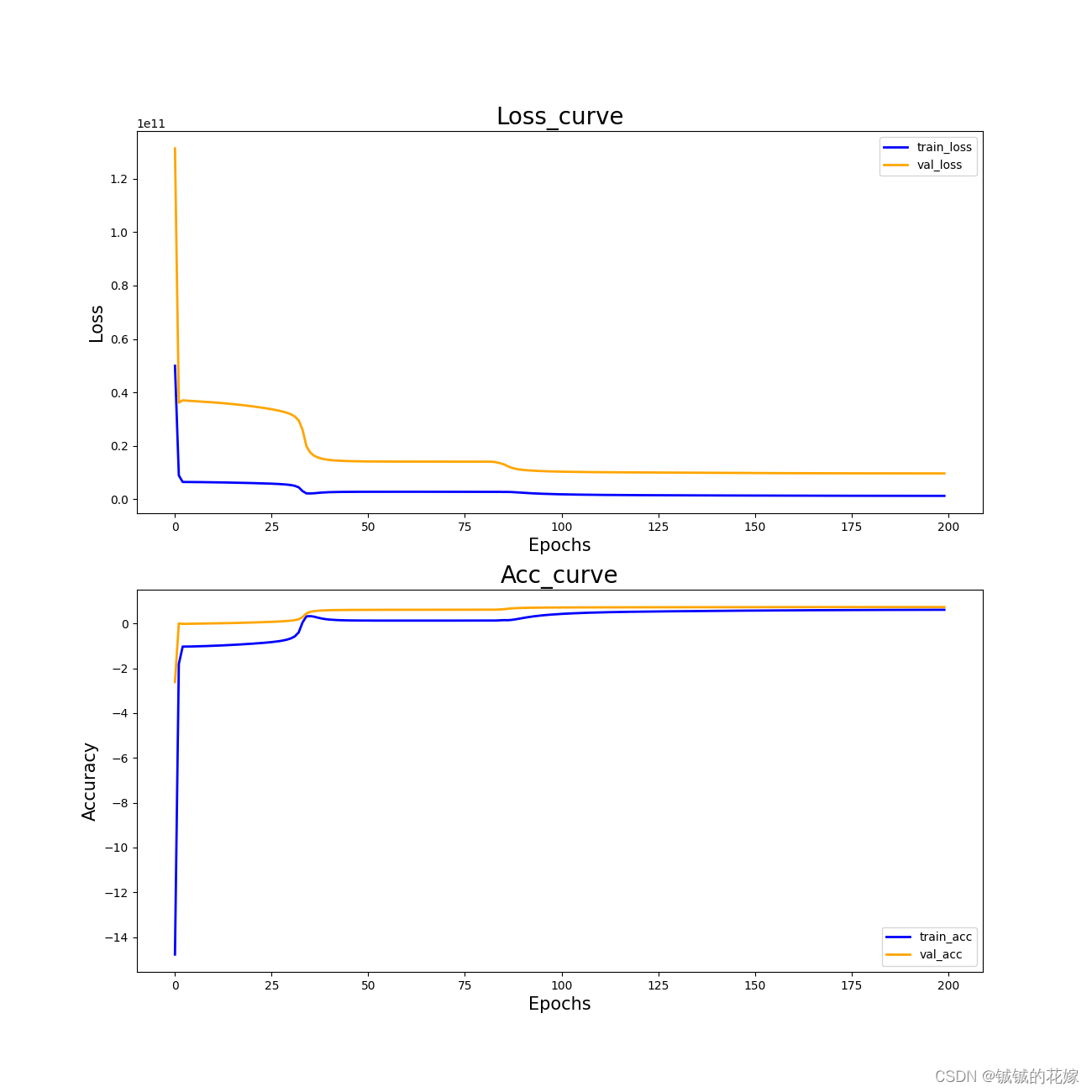
3.3 结果
训练ing……

R2 有 0.712,吊打隔壁全连接 MLP。

曲线如下(epoch到100的时候应该就差不多了)
4 代码(可直接食用)
记得一键三连噢~~