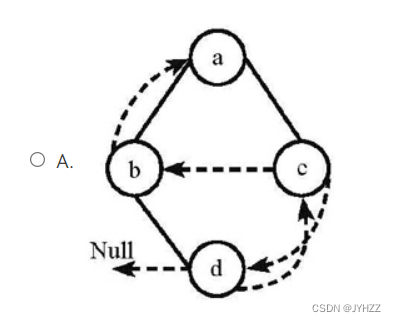
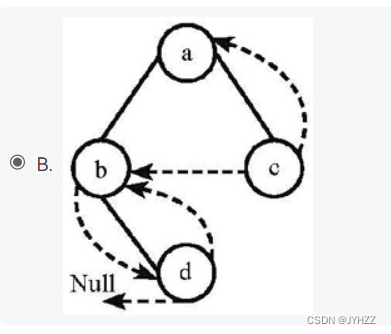
1.下列线索二叉树中(用虚线表示线索),符合后序线索树定义的是:B
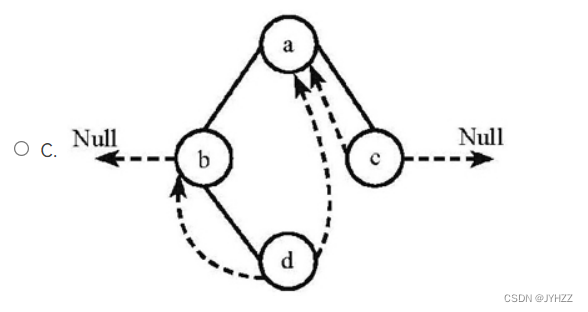
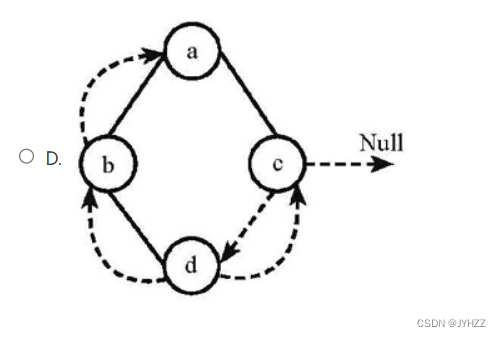
后序线索二叉树的构建流程就是:
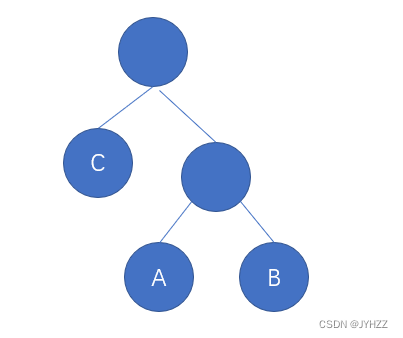
1.后序遍历二叉树:d b c a
2.第一个结点的前驱是NULL,即d的前驱,d的左孩子为NULL
3.按后序遍历的顺序来将空指针域指向对应的结点
d的后继(右孩子)指向b
b的前驱(左孩子)指向d
c的后继(右孩子)指向a
c的前驱(左孩子)指向b
2.引人线索二叉树的目的的是( A)。
A.加快查找结点的前驱或后继的速度
B.为了能在二叉树中方便地进行插人与侧除
C.为了能方便地找到双亲
D.使二叉树的遍历结果唯一
构建线索二叉树就是将空指针域指向对应结点的前驱或者后继,所以选A
3.若X是后序线索二叉树中的叶结点,且X存在左兄弟结点Y,则X的右线索指向的是(A)。
A.X的父结点
B.以Y为根的子树的最左下结点
C.X的左兄弟结点Y
D.以Y为根的子树的最右下结点
构造一个符合题意的二叉树就行

X的右线索指向的是X的后继,因为是后序线索二叉树,所以是X的父节点
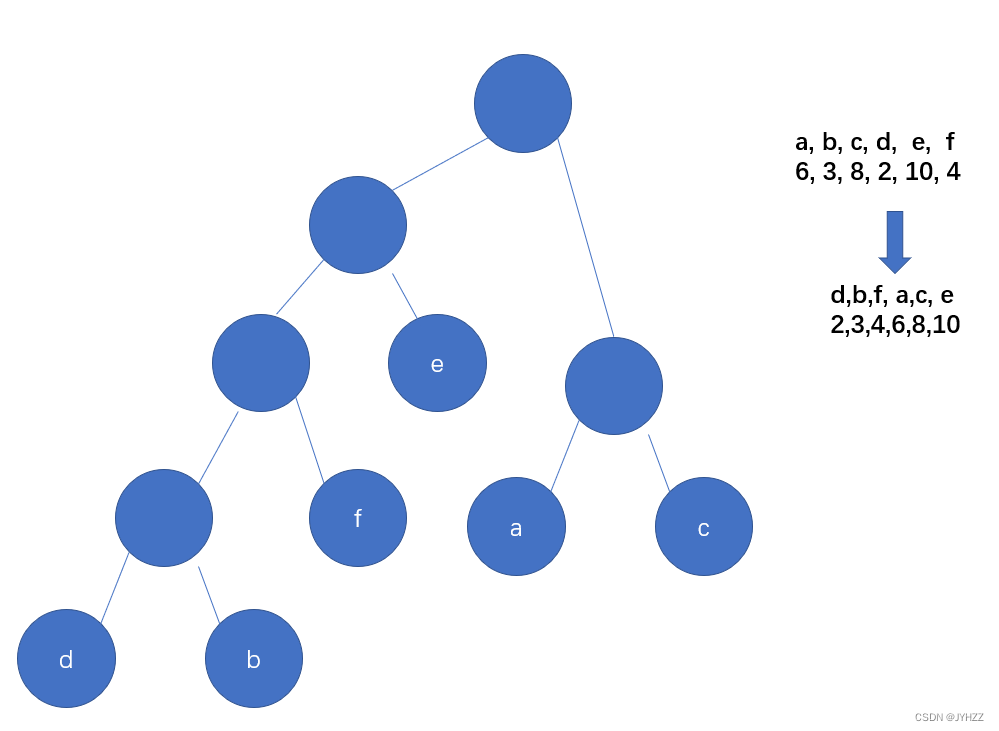
4.已知字符集{ a, b, c, d, e, f },若各字符出现的次数分别为{ 6, 3, 8, 2, 10, 4 },则对应字符集中各字符的哈夫曼编码可能是:A
A.00, 1011, 01, 1010, 11, 100
B.00, 100, 110, 000, 0010, 01
C.10, 1011, 11, 0011, 00, 010
D.0011, 10, 11, 0010, 01, 000
构造哈夫曼树其中之一,其余的就是交换左右子树。
5.对 n 个互不相同的符号进行哈夫曼编码。若生成的哈夫曼树共有 115 个结点,则 n 的值是:C
A.56
B.57
C.58
D.60
对n个数进行哈夫曼编码,那么就有n个叶结点,n-1个非叶结点,相加得115,即2*n-1=115,n=58
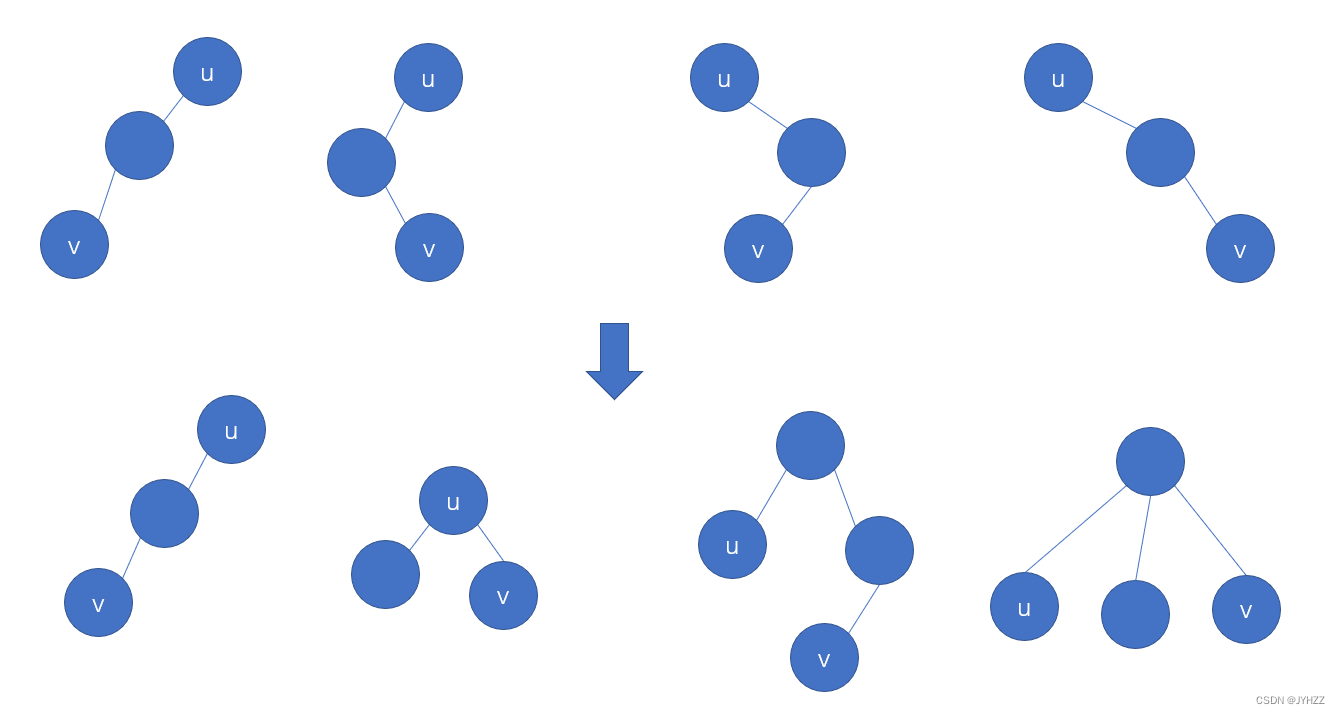
6.将森林转换为对应的二叉树,若在二叉树中,结点u是结点v的父结点的父结点,则在原来的森林中,u和v可能具有的关系是:B
- 父子关系; 2. 兄弟关系; 3. u的父结点与v的父结点是兄弟关系
A.只有2
B.1和2
C.1和3
D.1、2和3
根据题意,列出二叉树,还原为森林
7.对于一个有N个结点、K条边的森林,共有几棵树?A
A.N−K
B.N−K+1
C.N−K−1
D.不能确定
对于一棵树,有这样的性质:节点数-边数=1。
例如:
有5个结点,4条边
森林是0棵或有限棵不相交的树的集合,比如森林中有3棵树,那么每棵树的结点数比边数多1,那么三棵树的总结点数就比总边数多3。由此可得,对于一个有N个结点、K条边的森林,它有N-K棵树
8.设森林F中有三棵树,第一、第二、第三棵树的结点个数分别为M1,M2和M3。则与森林F对应的二叉树根结点的右子树上的结点个数是:C
A.M1
B.M1+M2
C.M2+M3
D.M3
森林F对应的二叉树根结点的左子树就是第一棵树,森林F对应的二叉树根结点的右子树是其余树,所以选C
9.由若干个二叉树组成的森林F中,叶结点总个数为N,度为2的结点总个数为M,则该集合中二叉树的个数为:B
A.M−N
B.N−M
C.N−M−1
D.无法确定
对于一棵非空二叉树,有这样的性质,若叶子结点数为a,度数为2的节点数为b,那么a=b+1
对于森林,若叶子结点数为N,度数为2的节点数为M,那么N-M=树的个数
10.若森林F有15条边、25个结点,则F包含树的个数是:C
A.8
B.9
C.10
D.11
和第7题一样
11.给定一有向图的邻接表如下。从顶点V1出发按深度优先搜索法进行遍历,则得到的一种顶点序列为:
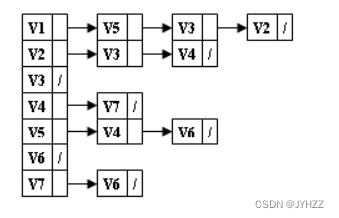
A.V1,V5,V4,V7,V6,V2,V3
B.V1,V2,V3,V4,V7,V6,V5
C.V1,V5,V4,V7,V6,V3,V2
D.V1,V5,V6,V4,V7,V2,V3
无向图邻接表的广度优先代码:
#include<iostream>
#include<queue>
#define MaxVerNum 100
using namespace std;
typedef int VertexType;
typedef struct node {
int adjvex;
struct node* next;
}EdgeNode;
typedef struct vnode {
VertexType vertex;
EdgeNode* firstedge;
}VertexNode;
typedef struct {
VertexNode AdhList[MaxVerNum];
int v_num;
int e_num;
}ALGraph;
ALGraph* CreatALGraph() {
ALGraph* G = (ALGraph*)malloc(sizeof(ALGraph));
printf("请输入顶点数和边数:\n");
scanf("%d,%d", &G->v_num, &G->e_num);
for (int i = 0; i < G->v_num; i++) {
cin >> G->AdhList[i].vertex;
G->AdhList[i].firstedge = NULL;
}
int p,q;
for (int i = 0; i < G->e_num; i++) {
scanf("%d,%d", &p, &q);
EdgeNode* newEdge = (EdgeNode*)malloc(sizeof(EdgeNode));
newEdge->adjvex = q;
newEdge->next = G->AdhList[p].firstedge;
G->AdhList[p].firstedge = newEdge;
newEdge = (EdgeNode*)malloc(sizeof(EdgeNode));
newEdge->adjvex = p;
newEdge->next = G->AdhList[q].firstedge;
G->AdhList[q].firstedge = newEdge;
}
return G;
}
int flag[MaxVerNum] = { 0 };
void BFS(ALGraph* G, int i) {
queue<int> q;
q.push(i);
printf("%d ", G->AdhList[i].vertex);
flag[i] = 1;
while (!q.empty()) {
int m = q.front();
q.pop();
EdgeNode* temp = G->AdhList[m].firstedge;
while (temp) {
if (!flag[temp->adjvex]) {
printf("%d ", temp->adjvex);
flag[temp->adjvex] = 1;
q.push(temp->adjvex);
}
temp = temp->next;
}
}
}
void BFStraverseAL(ALGraph* G) {
for (int i = 0; i < G->v_num; i++) {
if (!flag[i]) {
BFS(G, i);
}
}
}
/*
4,4
0
1
2
3
0,3
0,1
1,3
1,2
*/
int main()
{
ALGraph* G = CreatALGraph();
BFStraverseAL(G);
/*
for (int i = 0; i < G->v_num; i++) {
EdgeNode* temp = G->AdhList[i].firstedge;
printf("%d ", G->AdhList[i].vertex);
while (temp) {
printf("%d ", temp->adjvex);
temp = temp->next;
}
putchar('\n');
}
*/
return 0;
}
12.下列选项中,不是下图深度优先搜索序列的是 D

A.V1, V5, V4, V3, V2
B.V1, V3, V2, V5, V4
C.V1, V2, V5, V4, V3
D.V1, V2, V3, V4, V5
首先创建该图的邻接表存储
v1->v2->v3->v5(也可能是v1->v3->v2->v5)
v2->v5
v3->v2
v4->v3
v5->v4
然后看选项,都是从v1开始的,咱们也从v1开始:与v1相邻的结点可能是v2,v3或者v5,
假如是v1,v2,那么与v2的相邻的结点是v5,所以D是错的。
代码实现:
#include<iostream>
#define MAX 10
using namespace std;
//定义邻接表
typedef struct enode {
int edata;
struct enode* next;
};
typedef struct vnode {
int vdata;
struct enode* first;
};
typedef struct ALGraph {
struct vnode s[MAX];
int v_num, e_num;
};
ALGraph* creat() {
ALGraph* newALGpragh = (ALGraph*)malloc(sizeof(struct ALGraph));
printf("请输入顶点数与边数:\n");
scanf("%d,%d", &newALGpragh->v_num, &newALGpragh->e_num);
for (int i = 1; i <= newALGpragh->v_num; i++) {
scanf("%d", &newALGpragh->s[i].vdata);
newALGpragh->s[i].first = NULL;
}
for (int i = 0; i < newALGpragh->e_num; i++) {
int m, n;
scanf("%d,%d", &m, &n);
struct enode* temp = (enode*)malloc(sizeof(struct enode));
temp->edata = n;
temp->next = NULL;
temp->next = newALGpragh->s[m].first;
newALGpragh->s[m].first = temp;
}
return newALGpragh;
}
int flag[MAX];
void DFSTravesALG(ALGraph* G, int i) {
printf("%d ", i);
flag[i] = 1;
enode* temp = G->s[i].first;
while (temp) {
int j = temp->edata;
if (!flag[j]) {
DFSTravesALG(G, j);
}
temp = temp->next;
}
}
void DFS(ALGraph* G) {
for (int i = 1; i <= G->v_num; i++) {
if (!flag[i]) {
DFSTravesALG(G, i);
}
}
}
/*
5,7
1
2
3
4
5
1,2
1,3
1,5
2,5
3,2
4,3
5,4
*/
int main() {
ALGraph* newALGraph = creat();
printf("邻接表:\n");
for (int i = 1; i <= newALGraph->v_num; i++) {
printf("v%d:", newALGraph->s[i].vdata);
enode* temp = newALGraph->s[i].first;
while(temp) {
printf("%d ", temp->edata);
temp = temp->next;
}
printf("\n");
}
printf("深度优先搜索:\n");
DFS(newALGraph);
return 0;
}
13.给定无向带权图如下,以下哪个是从顶点 a 出发深度优先搜索遍历该图的顶点序列(多个顶点可以选择时按字母序)? C
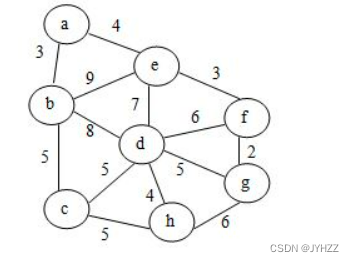
A.abecdfhg
B.abcdehgf
C.abcdefgh
D.abchgfde
12题是有向图,这个是无向图,做法一样
14.如果无向图G必须进行两次广度优先搜索才能访问其所有顶点,则下列说法中不正确的是:B
A.G肯定不是完全图
B.G中一定有回路
C.G一定不是连通图
D.G有2个连通分量
名词解释:
完全图:
也称简单完全图。假设一个图有n个顶点,那么如果任意两个顶点之间都有边的话,该图就称为完全图,有n(n-1)/2 条边。
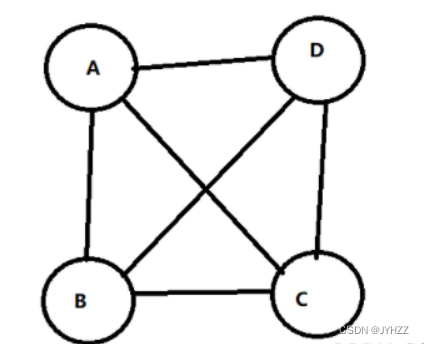
也就是有n个顶点,那么每一个顶点与其他n-1个顶点都要连上。
连通图(一般都是指无向图):
从顶点v到w有路径,就称顶点v和m连通。(路径是由顶点和相邻顶点序偶构成的边所形成的序列,其实就是一堆相连的顶点及其边)
也就是如果图中任意俩顶点都连通,则该图为连通图。
连通分量:
与连通图对应,一般书上说的都是特指无向图!!
极大连通子图是无向图的连通分量。
简单解释就是图中有几个不连通的部分就有几个连通分量
题干中的无向图G必须进行两次广度优先搜索才能访问其所有顶点就是在说下面代码的BFSTravseALG(ALGraph* G, int i)函数要执行两次,什么情况下会执行两次?
就是BFSTravseALG(ALGraph* G, int i)函数没能一次将Bflag的有效范围全部变为1
那么图便有不连通的部分,执行几次广度优先搜索就有几个不连通的部分,也就是有几个连通分量,D对;
因为有不连通的部分,所以不是完全图,A,C对;
不一定有回路,所以B错。
这是广度优先遍历的代码:
int Bflag[MAX];
void BFSTravseALG(ALGraph* G, int i) {
printf("%d ", i);
Bflag[i] = 1;
int queue[MAX];
int left = -1;
int right = -1;
queue[++right] = i;
while (left != right) {
int temp = queue[++left];
enode* q = G->s[temp].first;
while (q) {
int m = q->edata;
if (!Bflag[m]) {
printf("%d ", m);
Bflag[m] = 1;
queue[++right] = m;
}
q = q->next;
}
}
}
void BFS(ALGraph* G) {
for (int i = 1; i < G->v_num; i++) {
if (!Bflag[i]) {
BFSTravseALG(G, i);
}
}
}15.给定一有向图的邻接表如下。从顶点V1出发按广度优先搜索法进行遍历,则得到的一种顶点序列为:C
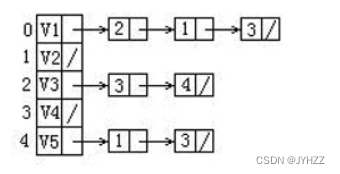
A.V1,V2,V3,V4,V5
B.V1,V2,V3,V5,V4
C.V1,V3,V2,V4,V5
D.V1,V4,V3,V5,V2
这里面邻接点中的数字代表的是数组的下标,比如2代表的是v3,不是v2
16.已知一个图的邻接矩阵如下,则从顶点V1出发按广度优先搜索法进行遍历,可能得到的一种顶点序列为:A

A.V1,V2,V3,V5,V4,V6
B.V1,V2,V4,V5,V6,V3
C.V1,V3,V5,V2,V4,V6
D.V1,V3,V5,V6,V4,V2
按着这个邻接矩阵,画出图或者邻接表就行
17.图的广度优先遍历类似于二叉树的:D
A.先序遍历
B.中序遍历
C.后序遍历
D.层次遍历
18.给定有权无向图的邻接矩阵如下,其最小生成树的总权重是:D
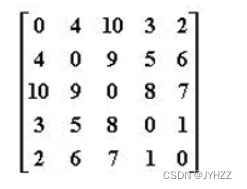
A.10
B.11
C.12
D.14
按着这个邻接矩阵,画出图,然后算一下就行。
19.给定有权无向图的邻接矩阵如下,其最小生成树的总权重是:C

A.20
B.22
C.8
D.15
20.给定有权无向图如下。关于其最小生成树,下列哪句是对的?A
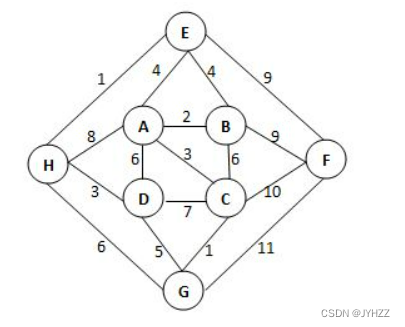
A.最小生成树不唯一,其总权重为23
B.最小生成树唯一,其总权重为20
C.边(B, F)一定在树中,树的总权重为23
D.边(H, G)一定在树中,树的总权重为20