目录
1. 关于遗传算法
2. 遗传算法的步骤
3. 代码实现
3.1 工具函数
3.1.1 目标函数
3.1.2 解码
3.1.3 交叉
3.1.4 变异
3.2 主函数部分
3.3 代码
4. 其他
1. 关于遗传算法
遗传算法是根据生物进化论提出的计算最优解的一种算法,核心思想是物竞天择,适者生存
网上关于遗传算法的讲解很多,本章会利用python实现遗传算法实现计算函数最大值,将其中的细节进行讨论
本章利用的函数为:y = x^2 ,定义域为0-10
关于遗传算法利用的其实是基因的遗传重组,所以这里每一个基因都是二进制的序列,例如10101
那二进制映射回定义域就是解码过程, start + (end - start) * tmp / (pow(2,length)-1) ,start 是定义域的左值,end 是定义域的右值,tmp是二进制序列,length 是二进制序列的长度。通过这样的计算就可以将二进制映射回给定的定义域中
那么二进制序列的长度如何定义?
是根据计算精度而言的,例如这里要计算的精度为0.01。那么就需要0.01->0.02->...->10.00中间共有10*10^2 = 1000个数字,那么需要的二进制就是10,因为2^10 = 1024可以保存1000个数字。那么二进制的序列长度就是 10
2. 遗传算法的步骤
接下来看看遗传算法的步骤:
这里只是根据自己实现的代码进行步骤分析,有些细节或者和网上实现不同的地方会在最后补充
1. 初始化种群 : 因为产生的二进制序列一般来说不是一个,这样是为了下面更好的交叉操作。并且,多个二进制序列也有利于找到最优的解
2. 解码 : 解码的意思就是将产生的二进制序列映射到对应的定义域当中,因为二进制产生的值很大,例如上述例子,定义域在0-10,精度为0.01,那么二进制长度为10,如果不进行映射的话,随便的一个二进制都会超过定义域10
当解码完成后,初始化种群已经全部变成在定义域当中的随机n(产生二进制序列的个数)个点
3. 计算适应度 :将定义域中的随机解码的点进行计算,例子中的y = x^2 被称为适应度函数
计算适应度其实就是计算这些值(x)对应的y,比如要求取最大值,那么看一下随机产生的x,哪一个y大,然后对较大的进行操作。这样反复操作的话,就可以找到最大值
4. 轮盘赌选取父系存活概率 : 当随机产生的n个点,计算完适应度函数后,会生成对应的n个函数值。函数值越大,我们说他越好(我们要计算最大值),那么他应该存活的概率就大。对应的方法是轮盘赌,例如产生的y值: 2 和 9,那么2/(2+9) 和 9/(2+9) 就是2和9存活的概率,这种就是轮盘赌。
注意:这只是概率,不是绝对的 9 > 2 ,就一定是 9 存活
5. 交叉 : 交叉就是根据父系的二进制,将随机的比特位进行交换的操作,这样遗传的思维就出现了。
6. 变异 : 变异是为了跳出极值,将子代的二进制编码,随机取反。0- >1,1->0
具体的实现方式在代码里面讲解
3. 代码实现
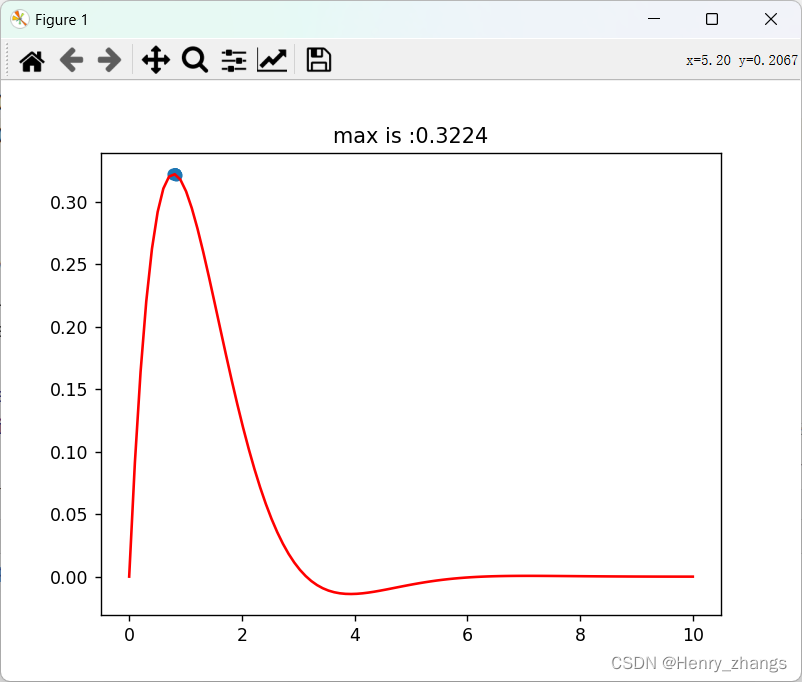
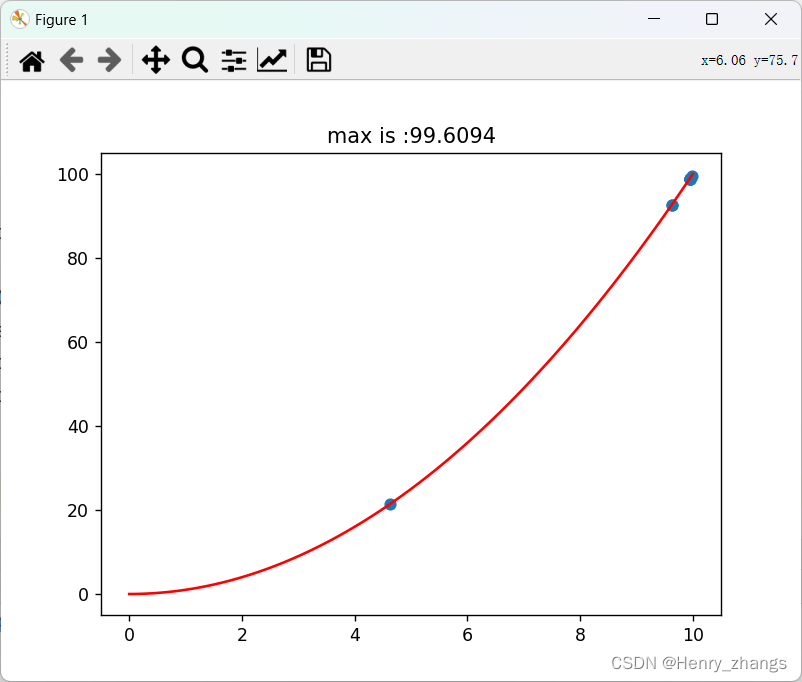
如图,本章遗传算法实现的是计算y = x^2 的最大值

关于遗传算法的定义在这:

其中,mutation_rate 是二进制序列变异的概率,这个不应该过大,要不然子代就完全和父代不一样,那么遗传算法也就失去了意义
parents_rate 是父代中保存的概率,例如这里总共有10个种群,0.3就会保存3个父代,这里保存的方式是通过轮盘赌实现
实现的效果为:
3.1 工具函数
为了代码的模块化,这里utils里面存放了四个函数
3.1.1 目标函数
也就是适应度函数
# 目标函数
def function(x):
# y = np.sin(x) * np.exp(-x)
y = x**2
return y
3.1.2 解码
decode 是根据传递的二进制序列矩阵bit_matrix(n*m,n是种群个数,m是二进制的长度) 进行编码,产生n个在start-end定义域中的十进制自变量
# 将二进制编码为十进制,并映射到定义域中
def decode(bit_matrix,num_group,start,end,length):
ret = np.zeros(num_group)
temp = [] # 保存转换的十进制数
for i in range(num_group):
tmp = int(''.join(map(lambda x:str(x),bit_matrix[i])),2) # 获得每一条染色体的十进制
ret[i] = start + (end - start) * tmp / (pow(2,length)-1) # 映射回原始的定义域
temp.append(tmp)
return temp,ret3.1.3 交叉
这里实现的方法有所不同
本章实现的遗传算法,种群数目是固定的 ,也就是说初始化是10个,那么父代保留了3个后,交叉产生的子代就只有7个,也就是代码中的count变量。
parents_groups 是父代的所有种群,而非保留之后的3个
实现交叉的方式为,将两组随机的二进制序列进行交叉。最后返回
# 交叉繁殖
def cross(count,parents_groups,length,cross_num=2):
childen = [] # 子代
while len(childen) != count: # 保证子代的数量和父代一样
index = np.random.choice(np.arange(length),cross_num,replace=False) # 随机交换cross_num个基因
male = parents_groups[np.random.randint(0,len(parents_groups+1))] # 从父代中随机挑选两个交叉繁殖
female = parents_groups[np.random.randint(0,len(parents_groups+1))]
childen_one = male.copy()
childen_two = female.copy()
childen_one[index] = female[index] # 交换父母双方的基因产生两个子代
childen.append(childen_one)
if len(childen) == count:
break
childen_two[index] = male[index]
childen.append(childen_two)
return np.array(childen)3.1.4 变异
变异是为了种群能够产生突变,这样随机产生的新的子代也许能够跳出极值
实现方式也很简单,num_mutation可以控制二进制变异的个数
# 变异
def mutation(children,mutation_rate,length,num_mutation=1):
children_mutation = []
for i in range(len(children)):
tmp = children[i]
if np.random.random() < mutation_rate:
index = np.random.choice(np.arange(length),num_mutation,replace=False)
for j in range(num_mutation): # 变异
if tmp[index[j]] == 1:
tmp[index[j]] = 0
else:
tmp[index[j]]= 1
children_mutation.append(tmp)
return np.array(children_mutation)3.2 主函数部分
有几点需要注意,计算适应度的时候,将它进行下面的操作,要不然轮盘赌选择的时候会报错。因为概率不能为负值

3.3 代码
主函数部分:
import numpy as np
import matplotlib.pyplot as plt
from utils import decode,function,cross,mutation
# 设定超参数
start,end = 0,10
length = 10 # 染色体长度 bit,精度
num_group = 10 # 种群数量
iteration_time = 2000 # 迭代次数
mutation_rate = 0.1 # 变异率
parents_rate = 0.3 # 父代中的保存个数(概率)
# 初始化二进制种群
init_group = np.random.randint(0,2,size=(num_group,length))
parents_group = init_group # 父代
# 迭代
decode_parents_group = 0
for i in range(iteration_time):
# 将二进制种群转为十进制,并映射到定义域中
_, decode_parents_group = decode(bit_matrix=parents_group, num_group=num_group, start=start, end=end, length=length)
# 计算种群适应度
f = function(decode_parents_group)
f = (f - np.min(f))+1e-8 # 防止 f 为负值或 0
select = np.random.choice(np.arange(num_group),int(num_group*parents_rate),replace=True,p=f/sum(f))
best_parents_group = parents_group[select] # 父代中的保留
count = len(parents_group) - len(best_parents_group) # 计算差值
# 交叉繁殖
children = cross(count=count, parents_groups=parents_group, length=length)
children = np.concatenate((best_parents_group, children))
# 变异
children = mutation(children=children,mutation_rate=mutation_rate,length=length)
parents_group = children
fun = function(decode_parents_group)
x = np.linspace(start,end,100)
plt.plot(x,function(x),color='r')
plt.scatter(decode_parents_group,function(decode_parents_group))
plt.title('max is :%.4f' % np.max(fun))
plt.show()
utils 部分:
import numpy as np
# 目标函数
def function(x):
# y = np.sin(x) * np.exp(-x)
y = x**2
return y
# 将二进制编码为十进制,并映射到定义域中
def decode(bit_matrix,num_group,start,end,length):
ret = np.zeros(num_group)
temp = [] # 保存转换的十进制数
for i in range(num_group):
tmp = int(''.join(map(lambda x:str(x),bit_matrix[i])),2) # 获得每一条染色体的十进制
ret[i] = start + (end - start) * tmp / (pow(2,length)-1) # 映射回原始的定义域
temp.append(tmp)
return temp,ret
# 交叉繁殖
def cross(count,parents_groups,length,cross_num=2):
childen = [] # 子代
while len(childen) != count: # 保证子代的数量和父代一样
index = np.random.choice(np.arange(length),cross_num,replace=False) # 随机交换cross_num个基因
male = parents_groups[np.random.randint(0,len(parents_groups+1))] # 从父代中随机挑选两个交叉繁殖
female = parents_groups[np.random.randint(0,len(parents_groups+1))]
childen_one = male.copy()
childen_two = female.copy()
childen_one[index] = female[index] # 交换父母双方的基因产生两个子代
childen.append(childen_one)
if len(childen) == count:
break
childen_two[index] = male[index]
childen.append(childen_two)
return np.array(childen)
# 变异
def mutation(children,mutation_rate,length,num_mutation=1):
children_mutation = []
for i in range(len(children)):
tmp = children[i]
if np.random.random() < mutation_rate:
index = np.random.choice(np.arange(length),num_mutation,replace=False)
for j in range(num_mutation): # 变异
if tmp[index[j]] == 1:
tmp[index[j]] = 0
else:
tmp[index[j]]= 1
children_mutation.append(tmp)
return np.array(children_mutation)
4. 其他
这里用很多地方和网上实现的不一致,还有一些地方自己也不是特别明白
例如,保留父代的时候,可以重复保留吗?
本章的方法是可以(改为False就可以不重复),这里个人认为,如果选择保留父代不重复的话,那么基本上保留的父代就是按照概率值从大到小进行保留,那么初始化不太好的时候,很容易掉入极值的坑里
select = np.random.choice(np.arange(num_group),int(num_group*parents_rate),replace=True,p=f/sum(f))其他的例如,如果变异率或者变异的个数过多的话,那么父代留给子代的信息就完全被破坏了,那么遗传的意义也就没有了
这里计算 y = np.sin(x) * np.exp(-x) 的结果为: