竞赛 - AcWing
一、完美数
4876. 完美数 - AcWing题库
1、题目
如果一个正整数能够被 2520 整除,则称该数为完美数。
给定一个正整数 n,请你计算 [1,n]范围内有多少个完美数。
输入格式
一个整数 n。
输出格式
一个整数,表示 [1,n] 范围内完美数的个数。
数据范围
前 3 个测试点满足 1≤n≤3000。
所有测试点满足 1≤n≤10¹⁸。
输入样例:
3000
输出样例:
12、思路
简单题,直接看代码
3、代码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
long n=sc.nextLong();
System.out.println(n/2520);
}
}
二、最大价值
4877. 最大价值 - AcWing题库
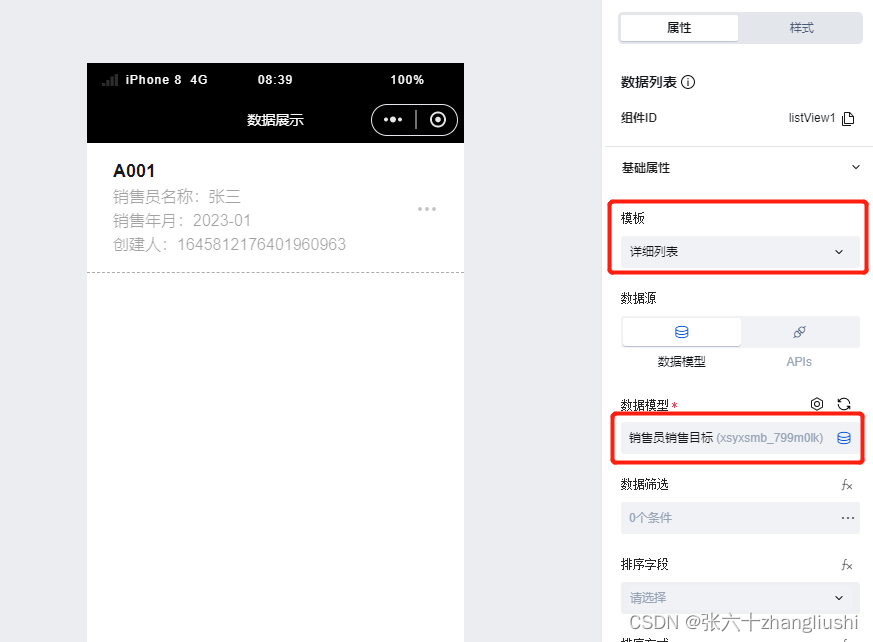
1、题目

数据范围
前 4个测试点满足 1≤n≤100,1≤m≤2。
所有测试点满足 1≤n≤1000,1≤m≤10,1≤lᵢ ,hᵢ ,vᵢ ,wᵢ ≤100。
输入样例1:
10 2 2 1
7 3 2 100
12 3 1 10
输出样例1:
241
输入样例2:
100 1 25 50
15 5 20 10
输出样例2:
2002、思路
看到题解里有一个写得特别好题解,大家就直接看吧!


背包问题——01背包|完全背包_冷兮雪的博客-CSDN博客
可以看看这篇01背包可以更好理解。
3、代码
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int v0 = sc.nextInt();
int w0 = sc.nextInt();
long[] count = new long[n + 1];//背包的容量
for (int i = 1; i <= m; i++) {//先遍历第1到m个物品
int l = sc.nextInt(), h = sc.nextInt(), v = sc.nextInt(), w = sc.nextInt();
int s = l / h;//计算物品i可以放几个
for (int j = n; j >= 0; j--) {//再倒序遍历背包容量
for (int k = 1; k <= s && k * v <= j; k++) {//1到s个物品i放与不放 取最大值
count[j] = Math.max(count[j], count[j - k * v] + (long) k * w);
}
}
}
long ans = 0;
for (int i = 0; i <= n; i++) {//遍历背包容量,先看是否可以放进,再取放与不放的最大值
if (i >= v0) {
count[i] = Math.max(count[i], count[i - v0] + w0);
}
//求出最大的背包价值
ans = Math.max(ans, count[i]);
}
System.out.println(ans);
}
}三、维护数组
4878. 维护数组 - AcWing题库
1、题目

输入格式
第一行包含 55 个整数 n,k,a,b,q。
接下来 q 行,每行描述一个操作,格式如题面所述。
输出格式
每个 2 p 操作,输出一行一个整数表示结果。
数据范围
前 33 个测试点满足 1≤k≤n≤10,1≤q≤10。
所有测试点满足 1≤k≤n≤2×10⁵,1≤b<a≤10000,1≤q≤2×10⁵,1≤x≤n,1≤y≤10000,1≤p≤n−k+1。
输入样例1:
5 2 2 1 8
1 1 2
1 5 3
1 2 1
2 2
1 4 2
1 3 2
2 1
2 3
输出样例1:
3
6
4
输入样例2:
5 4 10 1 6
1 1 5
1 5 5
1 3 2
1 5 2
2 1
2 2
输出样例2:
7
12、思路
要使所写代码时间复杂度在logN,我们需要使用树状数组。普通办法会运行超时。
想要详细了解树状数组可以看这篇博客
树状数组简单易懂的详解_FlushHip的博客-CSDN博客
想要快速了解写题思路可以看这篇博客
树状数组详解_萧何山的博客-CSDN博客
3、代码
import java.io.*;
public class Main {
static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
static int N = 200010, n, k, a, b, q;
static int[] tree1 = new int[N], tree2 = new int[N], d = new int[N];
static int lowbit(int x) {
return x & -x;
}
static void add(int[] tree, int x, int v) {
for (int i = x; i <= n; i += lowbit(i))
tree[i] += v;
}
static long query(int[] tree, int x) {
long ans = 0;
for (int i = x; i > 0; i -= lowbit(i))
ans += tree[i];
return ans;
}
public static void main(String[] args) throws Exception{
String[] s1 = in.readLine().split(" ");
n = Integer.parseInt(s1[0]);
k = Integer.parseInt(s1[1]);
a = Integer.parseInt(s1[2]);
b = Integer.parseInt(s1[3]);
q = Integer.parseInt(s1[4]);
while (q -- > 0) {
String[] s2 = in.readLine().split(" ");
int op = Integer.parseInt(s2[0]);
if (op == 1) { //增加 进行单点修改
int x = Integer.parseInt(s2[1]), y = Integer.parseInt(s2[2]);
add(tree1, x, Math.min(d[x] + y, b) - Math.min(d[x], b));
add(tree2, x, Math.min(d[x] + y, a) - Math.min(d[x], a));
d[x] += y;
}else { //查询 进行区间查询
int p = Integer.parseInt(s2[1]);
long sum = query(tree1, p - 1) + query(tree2, n) - query(tree2, p + k - 1);
out.println(sum);
}
}
out.flush();
}
}