🎉🎉🎉点进来你就是我的人了
博主主页:🙈🙈🙈戳一戳,欢迎大佬指点!
人生格言:当你的才华撑不起你的野心的时候,你就应该静下心来学习!欢迎志同道合的朋友一起加油喔🦾🦾🦾
目标梦想:进大厂,立志成为一个牛掰的Java程序猿,虽然现在还是一个🐒嘿嘿
谢谢你这么帅气美丽还给我点赞!比个心
目录
一、冒泡排序
二、直接插入排序
三、希尔排序
四、选择排序
选择排序优化前:
🐳选择排序优化后
五、堆排序
六、快速排序
1. hoare版本(左右指针法)
2. 挖坑法
3. 前后指针法
1. 快速排序的优化
2. 三数取中法(优化一)(对排序本身分割数据的一种优化)
3. 小区间优化(优化二)
4. 非递归实现快速排序
七、归并排序
1. 递归实现归并排序:
2.非递归实现归并排序:
3..归并排序的应用场景
八、计数排序(了解)
九、基数排序
十、桶排序
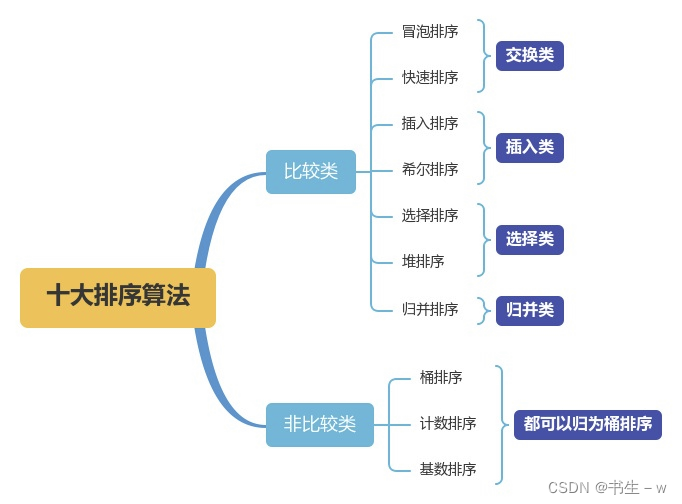
交换类:通过元素之间的两两交换来实现排序
插入类:将数分为2部分,依次将无序的数插入到有序的数列中
选择类:从待排序数列中找到最小值或者最大值元素,放到已拍好序的序列后面
计数排序和基数排序可以认为是桶排序的一种特殊实现,都不是通过元素之间的比较来实现排序的
一、冒泡排序
冒泡排序(Bubble Sort),是一种计算机科学领域的较简单的排序算法。
排序原理:
- 比较相邻的元素。如果前一个元素比后一个元素大,就交换这两个元素的位置。
- 对每一对相邻元素做同样的工作,从开始第一对元素到结尾的最后一对元素。最终最后位置的元素就是最大
- 每次比较得到的最大值下次就不用再比较了

实现代码:
- 时间复杂度分析:O(n^2)
- 空间复杂度分析:O(1)
- 稳定性:稳定
public class Test3 {
public static void bubbleSort(int[] array) {
for (int i = 0; i < array.length - 1; i++) {
//优化冒泡排序
//此处定义一个标志位判断在数组已经有序的情况下直退出
boolean flg = false;
for (int j = 0; j < array.length - 1 - i; j++) {
if(array[j] > array[j + 1]) {
swap(array, j, j + 1);
flg = true;
}
}
if(!flg) {
break;
}
}
}
private static void swap(int[] array, int j, int i) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
public static void main(String[] args) {
int[] array ={9,8,7,6,5,4,3,2,1};
bubbleSort(array);
System.out.println(Arrays.toString(array));
}
}
二、直接插入排序
直接插入排序(Insertion sort)是一种简单直观且稳定的排序算法。
排序原理:
1.把所有的元素分为两组,已经排序的和未排序的;
2.找到未排序的组中的第一个元素,向已经排序的组中进行插入;
3.倒叙遍历已经排序的元素,依次和待插入的元素进行比较,直到找到一个元素小于等于待插入元素,那么就把待插入元素放到这个位置,其他的元素向后移动一位;
步骤:
1.从第一个元素开始,该元素可以认为已经被排序
2.取下一个元素tem,从已排序的元素序列从后往前扫描
3.如果该元素大于tem,则将该元素移到下一位
4.重复步骤3,直到找到已排序元素中小于等于tem的元素
5.tem插入到该元素的后面,如果已排序所有元素都大于tem,则将tem插入到下标为0的位置
6.重复步骤2~5

实现代码:
- 时间复杂度分析:最坏情况下为O(N*2),此时待排序列为逆序,或者说接近逆序
最好情况下为O(N),此时待排序列为升序,或者说接近升序。 - 空间复杂度分析:只是开辟了一个 tmp 的变量 i,j,常数,即空间复杂度:O(1)
- 稳定性:稳定
- 该排序再数据越接近有序的情况,时间效率越高。
public class Test5 {
//直接插入排序
public static void insertSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
int tmp = arr[i];
int j;
for (j = i - 1; j >= 0 ; j--) {
if(arr[j] > tmp) {
//比插入的数大就向后移
arr[j + 1] = arr[j];
}else {
//比插入的数小,跳出循环
break;
}
}
//tmp放到比插入的数小的数的后面
arr[j + 1] = tmp;
}
}
public static void main(String[] args) {
int[] array ={9,8,7,6,5,4,3,2,1};
insertSort(array);
System.out.println(Arrays.toString(array));
}
}
三、希尔排序
是插入排序的优化,在排序过程中待排序数组根据gap增量进行插入排序,使子区间有序从而使整个待排序数组越来越有序。
● 具体思路
① 设置gap增量,这里gap的初始值为待排序数组的元素个数 / 2,每次以2倍的数量减少。
② 原本的插入排序间隔是1,这里每一组数据的排序间隔是gap,用gap进行分组排序。
③ gap越大,每组的元素个数就越少,反之,每组的元素个数越多。直到gap减少到1,则相当于让待排序数组进行直接插入排序。
注:希尔排序避免了当待排序数组为逆序时,直接插入排序达到最坏时间复杂度O(N^2)的情况,希尔排序是先根据gap增量对 待排序数组 进行预排序,最基本排序思路还是依次取出[gap,arr.length - 1]位置的元素在对应组内的有序区间中找到插入位置插入,所以说希尔排序是插入排序的优化。
静图分析:

动图如下: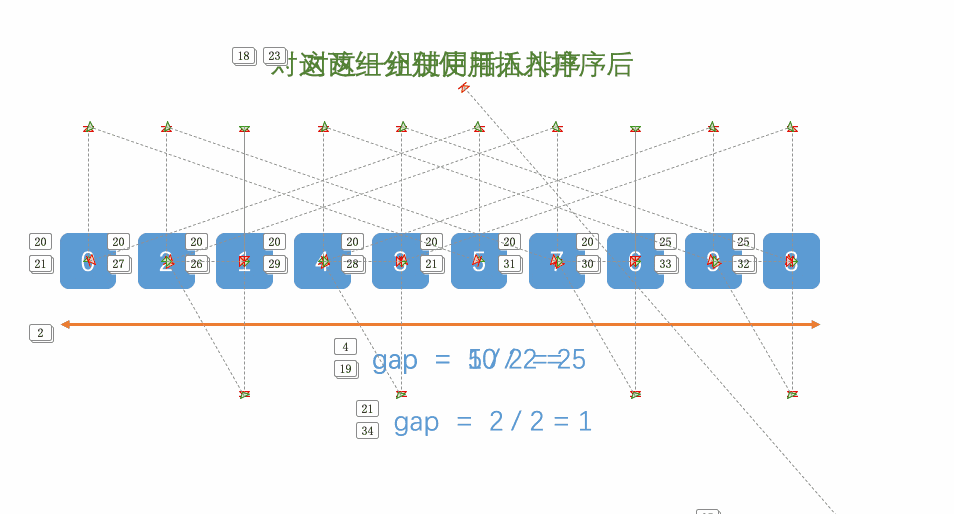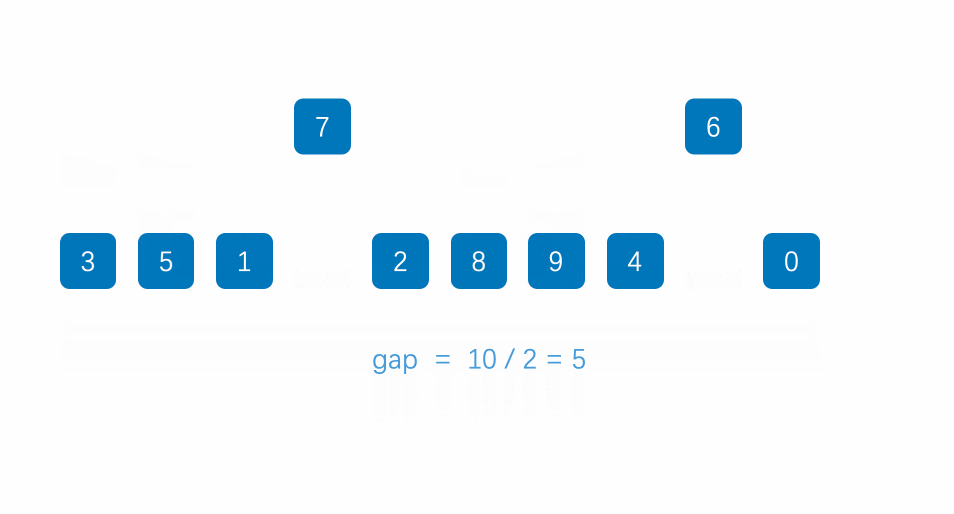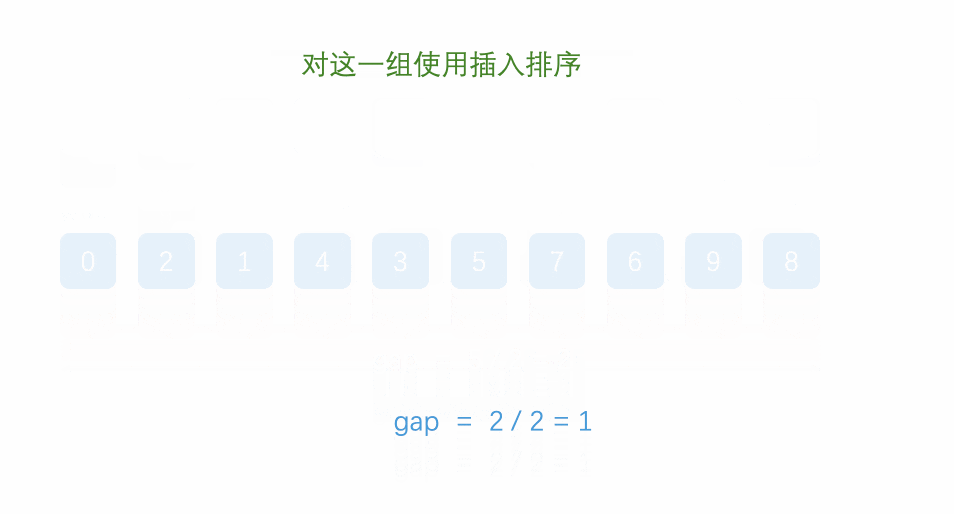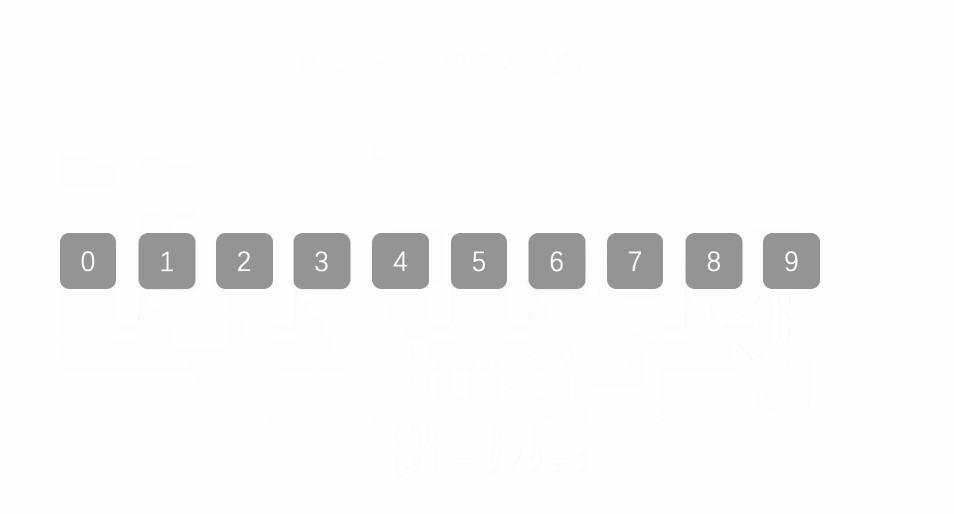
实现代码:
- 时间复杂度分析:希尔排序的时间复杂度不好分析, 这里我们就大概记一下,约为 O(n^1.3),感兴趣的话,可以查阅一下相关书籍。
- 空间复杂度分析:仍然开辟的是常数个变量,空间复杂度为 O(1)
- 稳定性:不稳定
public class Test4 {
public static void shellSort(int[] array) {
// gap初始值设置成数组长度的一半
int gap = array.length >> 1;
// gap 为 1 的时候直接插入排序
while (gap > 1) {
shell(array, gap);
gap >>= 1; // 更新 gap 值 等价于 -> gap /= 2;
}
//整体进行插入排序
shell(array, 1);
}
private static void shell(int[] array, int gap) {
for (int i = gap; i < array.length; i++) {
int tmp = array[i];
int j = i - gap;
for (; j >= 0; j -= gap) {
if (array[j] > tmp) {
//比插入的数大就向后移动gap,因为每一组数据元素之间的间隔大小是gap,
array[j + gap] = array[j];
} else {
//比插入的数小,跳出循环
break;
}
}
//tmp放到比插入的数小的数的后面
array[j + gap] = tmp;
}
}
public static void main(String[] args) {
int[] array ={9,8,7,6,5,4,3,2,1};
shellSort(array);
System.out.println(Arrays.toString(array));
}
}
四、选择排序
选择排序是一种简单直观的排序方法。
排序原理:
- 每一次遍历的过程中,都假定第一个索引处的元素是最小值,和其他索引处的值依次进行比较,如果当前索引处 的值大于其他某个索引处的值,则假定其他某个索引出的值为最小值,最后可以找到最小值所在的索引
- 交换第一个索引处和最小值所在的索引处的值

选择排序优化前:
- 时间复杂度分析: O(n^2)
- 空间复杂度分析:O(1)
- 稳定性:不稳定 实际开发中用的不多
public class Test6 {
//选择排序
public static void selectSort(int[] arr) {
/*判断数组为空或为一个元素的情况,即边界检查*/
if (arr == null || arr.length < 2) {
return;
}
/*每次要进行比较的两个数,的前面那个数的下标*/
for (int i = 0; i < arr.length - 1; i++) {
//min变量保存该趟比较过程中,最小元素所对应的索引,
//先假设前面的元素为最小元素
int minIndex = i;
/*每趟比较,将前面的元素与其后的元素逐个比较*/
for (int j = i + 1; j < arr.length; j++) {
//如果后面的元素小,将后面元素的索引极为最小值的索引
if(arr[j] < arr[minIndex]) {
minIndex = j;
}
}
//然后交换此次查找到的最小值和原始的最小值
swap(arr, i, minIndex);
}
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
public static void main(String[] args) {
int[] array ={9,8,7,6,5,4,3,2,1};
selectSort(array);
System.out.println(Arrays.toString(array));
}
}
🐳选择排序优化后
选择排序的优化思路一般是在一趟遍历中,同时找出最大值与最小值,放到数组两端,这样就能将遍历的趟数减少一半。第一次选择最大值与最小值,过程如下
实现代码:时间复杂度:O(N^2) 面试两种写法都差不多
public void selectSort(int[] array) {
int left = 0;
int right = array.length - 1;
while (left < right) {
int maxIndex = left;
int minIndex = left;
// i = left + 1 -> 每次找最大最小值下标的时候, 可以不用算默认给的最大值和最小值下标
for (int i = left + 1; i <= right; i++) {
if (array[i] > array[maxIndex]) {
maxIndex = i;
}
if (array[i] < array[minIndex]) {
minIndex = i;
}
}
swap(array, minIndex, left);
// 如果最大值为 left 的位置情况的话, 走到这, 最大值已经被交换到 min 位置上了
if (maxIndex == left) {
// 更新最大值的位置
maxIndex = minIndex;
}
swap(array, maxIndex, right);
left++;
right--;
}
}五、堆排序
排序思想:
首先将待排序的数组构造成一个大根堆,此时,整个数组的最大值就是堆结构的顶端
将顶端的数与末尾的数交换,此时,末尾的数为最大值,剩余待排序数组个数为n-1
将剩余的n-1个数再调整为大根堆,再将顶端数与n-1位置的数交换,如此反复执行,便能得到有序数组

实现代码:
- 时间复杂度分析:建堆的时间复杂度优先级队列那期有说过为 O(n),排序调整堆的时候,一共要调整 n-1 次,每次向下调整的时间复杂度是 logn,所以即 logn(n - 1),即 O(n*logn),加上面建堆的时间复杂度:O(n) + O(n*logn),最终时间复杂度也就是:O(n*logn)。
- 空间复杂度分析:O(1)
- 稳定性:不稳定
public class Test2 {
//堆排序
public static void heapSort(int[] array) {
createHeap(array);//O(N)
int end = array.length - 1;
//O(N*log(N))
while(end > 0) {
swap(array, 0, end);
//从0下标开始调整,向下调整的结束条件是小于end,所以下标end的位置不参与调整
shiftDown(array, 0, end);
end--;
}
}
//向下调整 O(log(N))
private static void shiftDown(int[] array, int root, int len) {
int child = 2 * root + 1;
while(child < len) {
if(child + 1 < len && array[child] < array[child + 1]) {
child++;
}
if(array[child] > array[root]) {
swap(array, child, root);
root = child;
child = 2 * root + 1;
} else {
break;
}
}
}
//建大根堆 O(n)
private static void createHeap(int[] array) {
for (int p = (array.length-1-1)/2; p >= 0 ; p--) {
shiftDown(array, p, array.length);
}
}
private static void swap(int[] array, int child, int root) {
int tmp = array[child];
array[child] = array[root];
array[root] = tmp;
}
public static void main(String[] args) {
int[] array ={9,8,7,6,5,4,3,2,1};
heapSort(array);
System.out.println(Arrays.toString(array));
}
}
六、快速排序
快速排序是对冒泡排序的一种改进。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
排序原理:
- 首先设定一个分界值,通过该分界值将数组分成左右两部分;
- 将大于或等于分界值的数据放到到数组右边,小于分界值的数据放到数组的左边。此时左边部分中各元素都小于或等于分界值,而右边部分中各元素都大于或等于分界值;
- 然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理
- 重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当
左侧和右侧两个部分的数据排完序后,整个数组的排序也就完成了。
1. hoare版本(左右指针法)
思路:
1、选出一个key,一般是最左边或是最右边的。
2、定义一个L和一个R,L从左向右走,R从右向左走。(需要注意的是:若选择最左边的数据作为key,则需要R先走;若选择最右边的数据作为key,则需要L先走)。
3、在走的过程中,若R遇到小于key的数,则停下,L开始走,直到L遇到一个大于key的数时,将L和R的内容交换,R再次开始走,如此进行下去,直到L和R最终相遇,此时将相遇点的内容与key交换即可。(选取最左边的值作为key)
4.此时key的左边都是小于key的数,key的右边都是大于key的数
5.将key的左序列和右序列再次进行这种单趟排序,如此反复操作下去,直到左右序列只有一个数据,或是左右序列不存在时,便停止操作,此时此部分已有序
单趟动图如下:
实现代码:
public class Test8 {
//快速排序
public static void quickSort(int[] array) {
quick(array,0,array.length - 1);
}
public static void quick(int[] array,int start, int end) {
if(start >= end) { // 为什么要大于end?如果是有序的情况,== 就会失效
return;
}
int pivot = partition(array,start,end);
quick(array,0,pivot - 1);
quick(array,pivot+1,end);
}
//hoare法
private static int partition(int[] array,int left,int right) {
int tmp = array[left];
int i = left;
while (left < right) { // 一趟排序
while (left< right && array[right] >= tmp) {
right--;
}
while (left< right && array[left] <= tmp) {
left++;
}
swap(array,left,right);
}
swap(array,left,i);
return left;
}
private static void swap(int[] array, int i, int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
public static void main(String[] args) {
int[] array ={9,8,7,6,5,4,3,2,1};
quickSort(array);
System.out.println(Arrays.toString(array));
}
}
2. 挖坑法
思路:
挖坑法思路与hoare版本(左右指针法)思路类似
1.选出一个数据(一般是最左边或是最右边的)存放在key变量中,在该数据位置形成一个坑
2、还是定义一个L和一个R,L从左向右走,R从右向左走。(若在最左边挖坑,则需要R先走;若在最右边挖坑,则需要L先走)
过程:
(1)定义left、right并赋上相应的下标,记录当前left下标所对应的元素为tmp
(2)左边的left向右走、右边的right向左走。right先走,right找到比tmp小的值停下来,将right所在位置的元素赋给left所在的位置。left找到比tmp大的值停下来,将left所在位置的元素赋给right所在的位置。
(3)当left>=right时,将tmp的值赋给left所在的位置,返回left
(4)以left下标右边和左边为新的待排序数组继续执行1~3,直到整个数组完成排序。
单趟动图如下:
实现代码:
public class Test7 {
//快速排序
public static void quickSort(int[] array) {
quick(array,0,array.length-1);
}
private static void quick(int[] array, int start, int end) {
if(start >= end) {
return;
}
int pivot = partition(array,start,end);
quick(array,start,pivot-1);
quick(array,pivot+1,end);
}
//挖坑法
private static int partition(int[] array, int left, int right) {
int tmp = array[left];
while (left < right) { // 一趟排序
while (left < right && array[right] >= tmp) {
right--;
}
array[left] = array[right];
while (left < right && array[left] <= tmp) {
left++;
}
array[right] = array[left];
}
array[left] = tmp;
return left;
}
private static void swap(int[] array, int i, int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
public static void main(String[] args) {
int[] array ={9,8,7,6,5,4,3,2,1};
quickSort(array);
System.out.println(Arrays.toString(array));
}
}
3. 前后指针法
思路:
1、选出一个key,一般是最左边或是最右边的。
2、起始时,prev指针指向序列开头,cur指针指向prev+1。
3、若cur指向的内容小于key,则prev先向后移动一位,然后交换prev和cur指针指向的内容,然后cur指针++;若cur指向的内容大于key,则cur指针直接++。如此进行下去,直到cur到达end位置,此时将key和++prev指针指向的内容交换即可。
经过一次单趟排序,最终也能使得key左边的数据全部都小于key,key右边的数据全部都大于key。
然后也还是将key的左序列和右序列再次进行这种单趟排序,如此反复操作下去,直到左右序列只有一个数据,或是左右序列不存在时,便停止操作

实现代码:
public class Test9 {
//快速排序
public static void quickSort(int[] array) {
quick(array,0,array.length - 1);
}
public static void quick(int[] array,int start, int end) {
if(start >= end) { // 为什么要大于end?如果是有序的情况,== 就会失效
return;
}
int pivot = partition(array,start,end);
quick(array,0,pivot - 1);
quick(array,pivot+1,end);
}
//前后指针法 【了解即可】
private static int partition(int[] array,int left,int right) {
int prev = left ;
int cur = left+1;
while (cur <= right) {
if(array[cur] < array[left] && array[++prev] != array[cur]) {
swap(array,cur,prev);
}
cur++;
}
swap(array,prev,left);
return prev;
}
private static void swap(int[] array, int i, int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
public static void main(String[] args) {
int[] array ={9,8,7,6,5,4,3,2,1};
quickSort(array);
System.out.println(Arrays.toString(array));
}
}
1. 快速排序的优化
通过上面的测试我们发现,当给一组有序且很大的数据时,如果用快速排序就会造成栈溢出,溢出的原因就是因为快速排序在递归的时候要开辟内存空间,而递归的次数受树高度的影响。给定一组有序序列,在快排时就等同于只有左树或者只有右树,这样递归的次数就是这个序列的长度,因此给定的序列越大,递归次数越多就会越容易栈溢出。
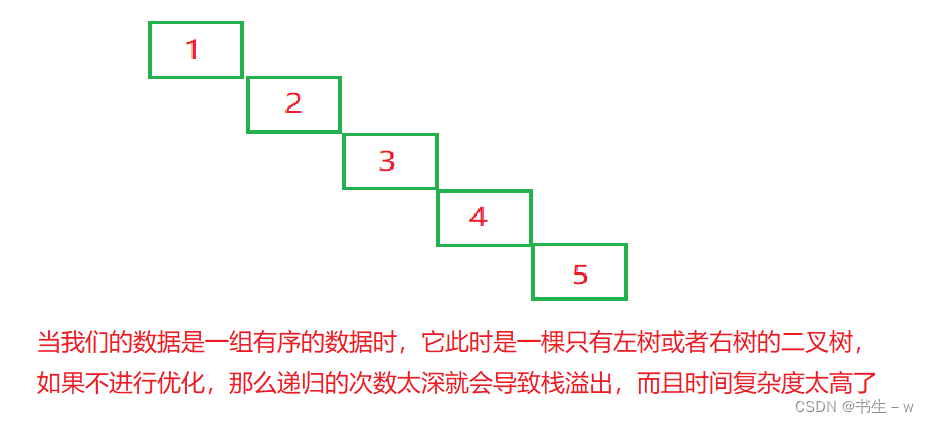
2. 三数取中法(优化一)(对排序本身分割数据的一种优化)

实现代码:
//三数取中法找基准值
private int medianOfThreeIndex(int[] array, int left, int right) {
int mid = left + (right - left) >>> 1;
if(array[left] < array[right]) {
if(array[mid] < array[left]) {
return left;
} else if(array[mid] > array[right]) {
return right;
} else {
return mid;
}
} else {
//此时array[left] > array[right
if(array[mid] > array[left]) {
return left;
} else if(array[mid] < array[right]) {
return right;
} else {
return mid;
}
}
}
public void quick(int[] array, int left, int right) {
if(left >= right) return;
//在找基准之前先调整数据是数据尽量对半分
int index = medianOfThreeIndex(array, left, right);
swap(array, left, index);
int pivot = partitionHole(array, left, right);
quick(array, left, pivot - 1);
quick(array, pivot + 1, right);
}3. 小区间优化(优化二)
数据量大的时候,分割到区间越小,则表示数据越接近有序了,前面我们认识了一个数据越接近有序效率越快的排序,那就是直接插入排序,所以我们可以进行小区间优化,那么简单来说,就是当区间的数据个数小于某个值的时候,采用直接插入排序算法。

实现代码:
private void quick(int[] array, int left, int right) {
if (left >= right) {
return;
}
// 小区间优化 -> 如果待排序的数据小于15个,我们直接使用直接插入排序
if ((right - left + 1) < 15) {
//直接插入排序
insertSort(array);
return;
}
// 三数取中
int mid = findMidValOfIndex(array, left, right);
swap(array, left, mid);
int pivot = partitionHoare(array, left, right);
quick(array, left, pivot - 1);
quick(array, pivot + 1, right);
}- 时间复杂度分析:在我们有了三数取中优化的情况下,可以达到 O(n*logn),如果没有三数取中,极端最坏的情况下,能达到 O(n^2),但是我们通常说的快排都是优化过的,也就是 O(n*logn)。
- 空间复杂度分析:每次递归都会压栈,随之开辟空间,那么快排类似于二叉树的前序遍历,左子树遍历完了,再有右子树,也就是会压栈,也会出栈,那么最大压栈多少呢?显然是树的高度,即 O(logn)。
- 稳定性:不稳定
- 快速排序整体的综合性能和使用场景都是比较好的
4. 非递归实现快速排序
我们需要用到栈
我们之前是在已经确定基准点之后,对剩余的区间递归进行同样的操作
我们现在创建一个栈,把剩余区间的左、右位置的下标分别放入栈中,如图是已经找到一个基准6的情况
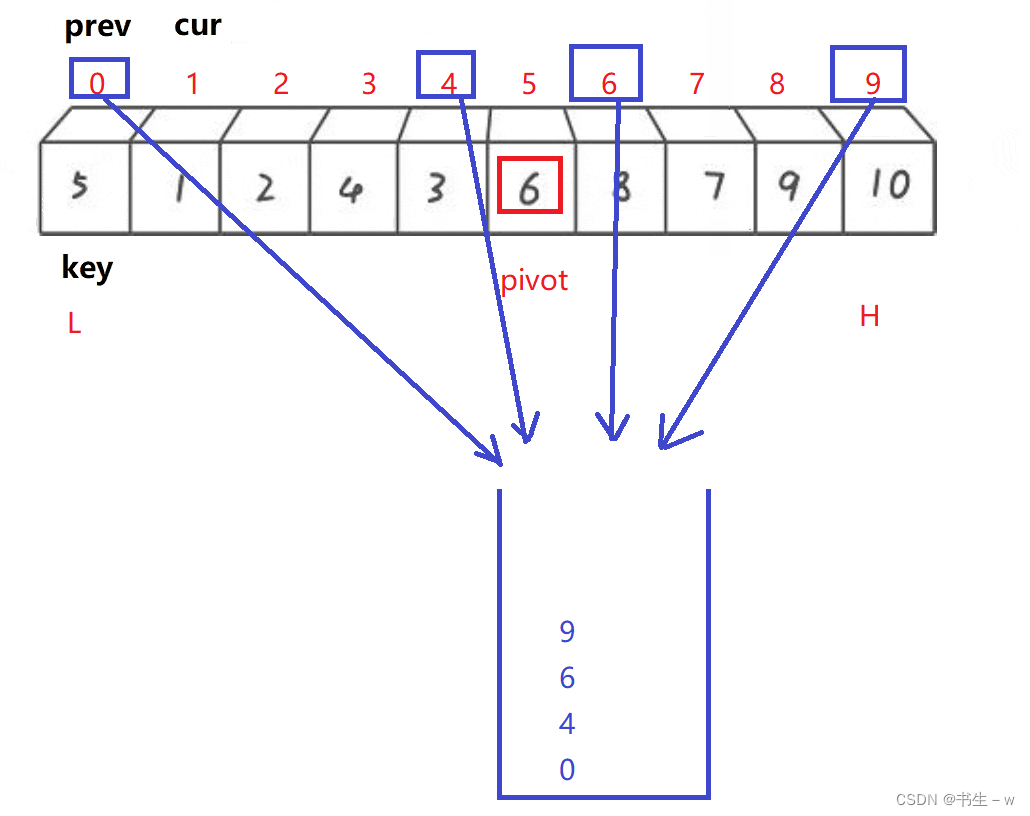
然后弹出下标9给H,再弹出一个下标6给L,根据新的L和H的区间找到新的基准,再重复上面的操作
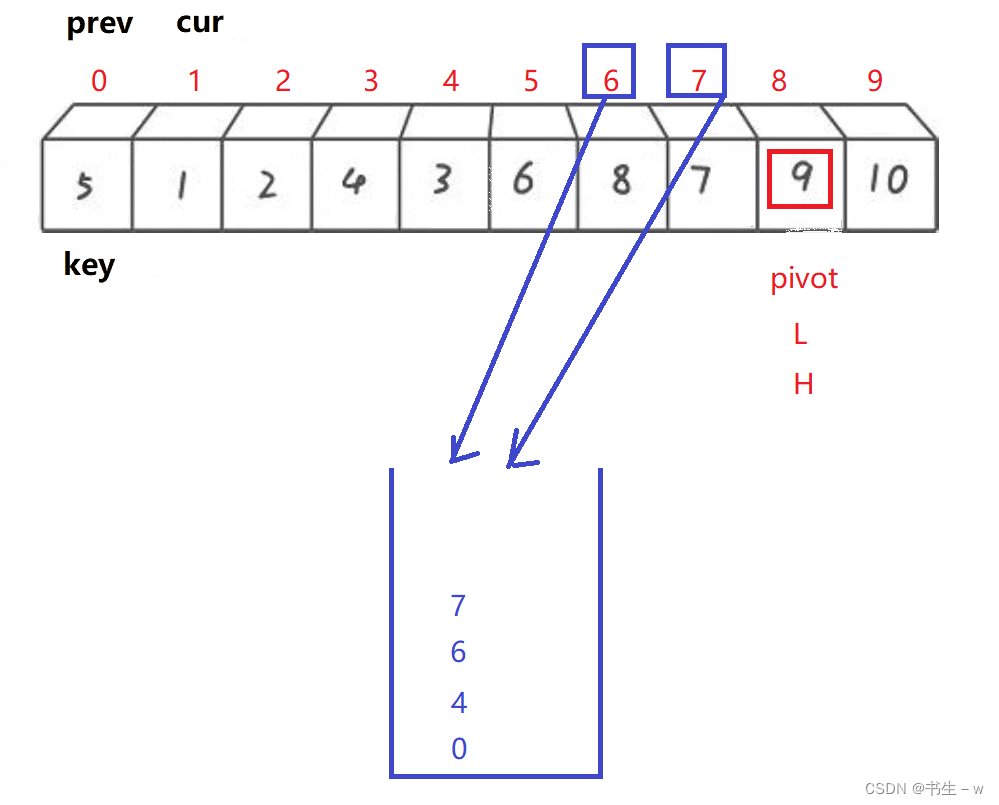
实现代码:
public class Test10 {
//快速排序(非递归)
public static void quickSort(int[] array){
int left =0;
int right =array.length-1;
Deque<Integer> stack = new LinkedList<>();
int pivot = partition(array,left,right);
if(pivot > left+1){
//说明左边有两个或两个以上数据
stack.push(left);
stack.push(pivot-1);
}
//说明右边有两个或两个以上数据
if(pivot < right-1){
stack.push(pivot+1);
stack.push(right);
}
while (!stack.isEmpty()){
right = stack.pop();
left = stack.pop();
pivot = partition(array,left,right);
if(pivot > left+1){
//说明左边有两个或两个以上数据
stack.push(left);
stack.push(pivot-1);
}
if(pivot < right-1){
stack.push(pivot+1);
stack.push(right);
}
}
}
//挖坑法
private static int partition(int[] array, int left, int right) {
int tmp = array[left];
while (left < right) { // 一趟排序
while (left < right && array[right] >= tmp) {
right--;
}
array[left] = array[right];
while (left < right && array[left] <= tmp) {
left++;
}
array[right] = array[left];
}
array[left] = tmp;
return left;
}
public static void main(String[] args) {
int[] array ={9,8,7,6,5,4,3,2,1};
quickSort(array);
System.out.println(Arrays.toString(array));
}
}
七、归并排序
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
排序原理:
- 尽可能的一组数据拆分成两个元素相等的子组,并对每一个子组继续拆分,直到拆分后的每个子组的元素个数是 1为止。
- 将相邻的两个子组进行合并成一个有序的大组;
- 不断的重复步骤2,直到最终只有一个组为止
静图分析:
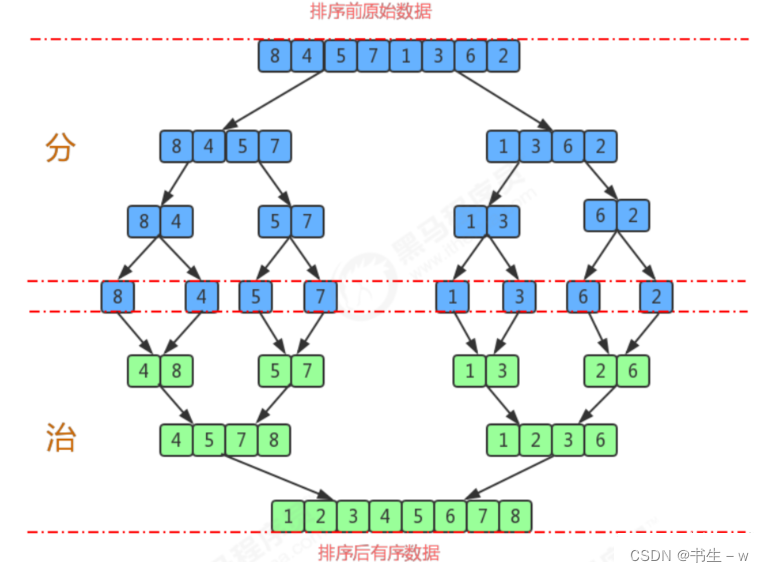
动图演示:

1. 递归实现归并排序:
- 时间复杂度:O(N*logN)
- 空间复杂度:最多会开辟数组长度个空间即 O(N)
- 稳定性:稳定
public class MergeSort {
//归并排序
public static void mergeSort(int[] array, int left, int right){
if (left >= right) {
return;
}
int mid = (left+right) / 2;
//向左递归分解
mergeSort(array, left, mid);
//向右递归分解
mergeSort(array, mid + 1, right);
//排序 合并
merge(array, left, right, mid);
}
//排序 合并子序列
public static void merge(int[] array, int start, int end, int mid){
int s1 = start; //初始化s1,左边有序序列的初始索引
int s2 = mid + 1; //初始化s2,右边有序序列的初始索引
int k = 0; //指向tmp数组的当前索引
int[] tmp =new int[end -start +1];
while (s1 <= mid && s2 <= end) {
if(array[s1] <= array[s2]) {
tmp[k++] =array[s1++];
}else {
tmp[k++] =array[s2++];
}
}
//将剩余子序列中的元素挪到新数组中
while (s1 <= mid) {
tmp[k++] =array[s1++];
}
while (s2 <= end) {
tmp[k++] =array[s2++];
}
for (int i = 0; i < tmp.length; i++) {
//i + start 是防止拷贝第二段子序列时,覆盖第一段,且达不到想到的效果
array[i+start] =tmp[i];
}
}
public static void main(String[] args) {
int[] array = {9,8,7,6,5,4,3,2,1};
mergeSort(array,0, array.length-1);
System.out.println(Arrays.toString(array));
}
}2.非递归实现归并排序:
解题思路:
利用将数组如树进行拆开后,回到原来的模样,由1个单独的数据,变成2个有序的数据,变成4个有序的数据,直至当它变成与原待排序列等长的数据为止,时间复杂度:O(N*logN)
public class MergeSort2 {
//非递归实现归并排序
public static void mergeSort(int[] array) {
int gap = 1;
while (gap < array.length) {
// i += gap * 2 当前gap组的时候,去排序下一组
for (int i = 0; i < array.length; i += gap * 2) {
int left = i;
int mid = left+gap-1;//有可能会越界
if(mid >= array.length) {
mid = array.length-1;
}
int right = mid+gap;//有可能会越界
if(right>= array.length) {
right = array.length-1;
}
merge(array,left,right,mid);
}
//当前为2组有序 下次变成4组有序
gap *= 2;
}
}
//排序 合并子序列
public static void merge(int[] array, int start, int end, int mid){
int s1 = start; //初始化s1,左边有序序列的初始索引
int s2 = mid + 1; //初始化s2,右边有序序列的初始索引
int k = 0; //指向tmp数组的当前索引
int[] tmp =new int[end -start +1];
while (s1 <= mid && s2 <= end) {
if(array[s1] <= array[s2]) {
tmp[k++] =array[s1++];
}else {
tmp[k++] =array[s2++];
}
}
//将剩余子序列中的元素挪到新数组中
while (s1 <= mid) {
tmp[k++] =array[s1++];
}
while (s2 <= end) {
tmp[k++] =array[s2++];
}
for (int i = 0; i < tmp.length; i++) {
//i + start 是防止拷贝第二段子序列时,覆盖第一段,且达不到想到的效果
array[i+start] =tmp[i];
}
}
public static void main(String[] args) {
int[] array = {9,8,7,6,5,4,3,2,1};
mergeSort(array);
System.out.println(Arrays.toString(array));
}
}
3..归并排序的应用场景
海量数据的排序问题:我们有100G的数据待排序,内存只有一个G,我们应该怎么办???
因为内存中因为无法把所有数据全部放下,所以需要外部排序,而归并排序是最常用的外部排序
1. 先把文件切分成 200 份,每份 512 M
2. 分别对 512 M 排序,因为内存已经可以放的下,所以任意排序方式都可以
3. 进行 2路归并,同时对 200 份有序文件做归并过程,最终结果就有序了
八、计数排序(了解)
思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤
1. 统计相同元素出现次数
2. 根据统计的结果将序列回收到原来的序列中
动图演示: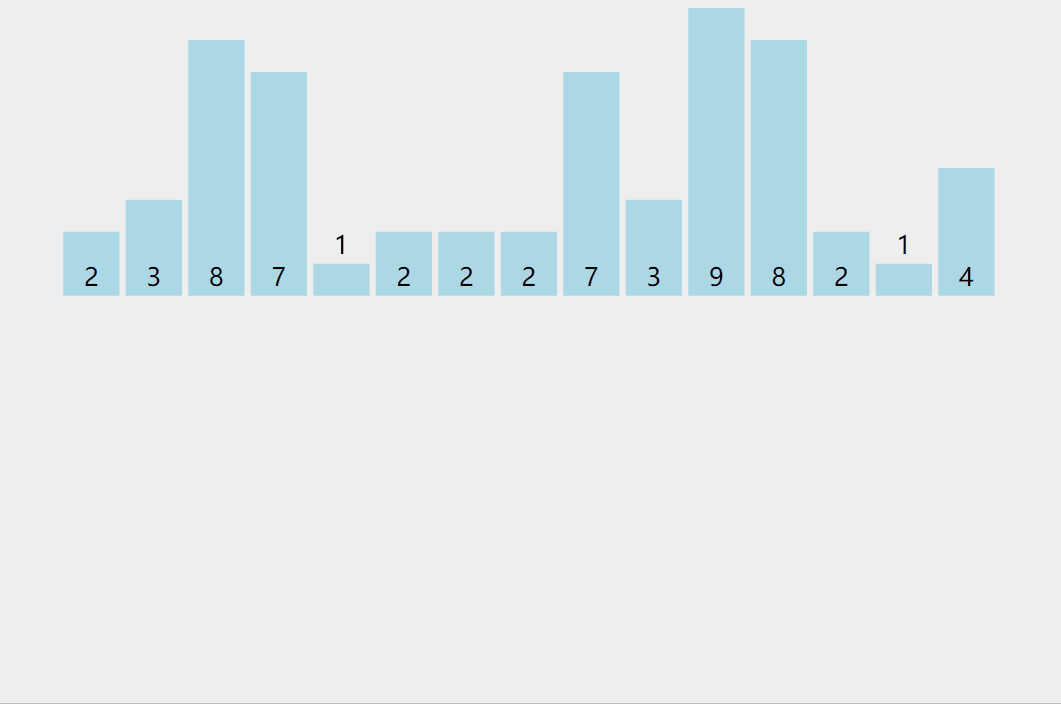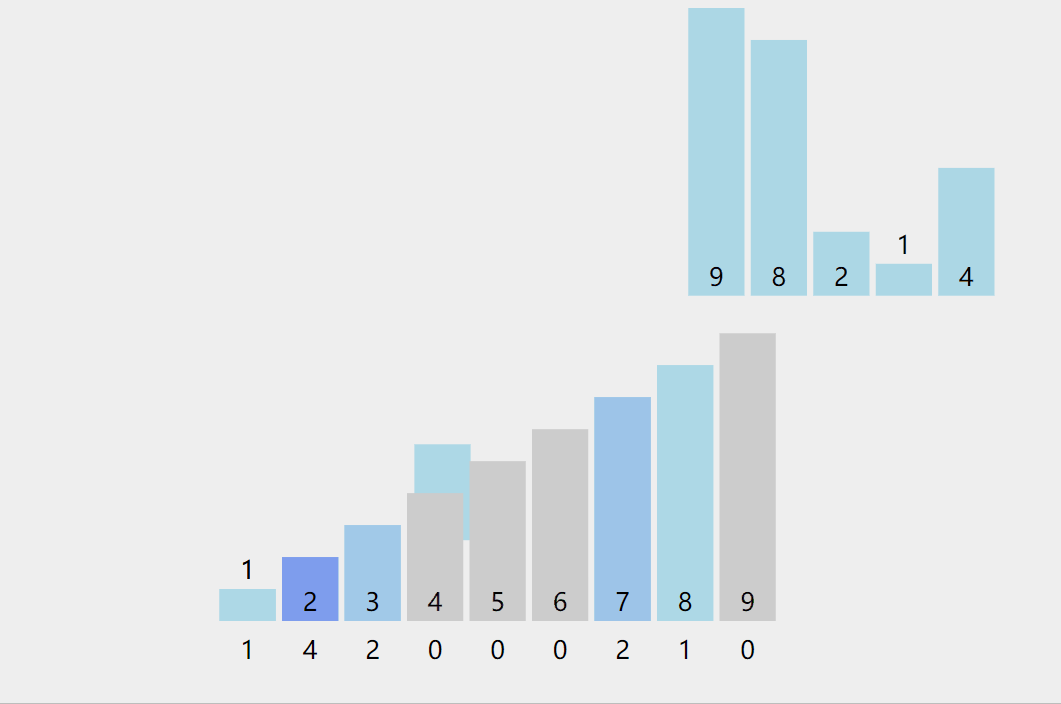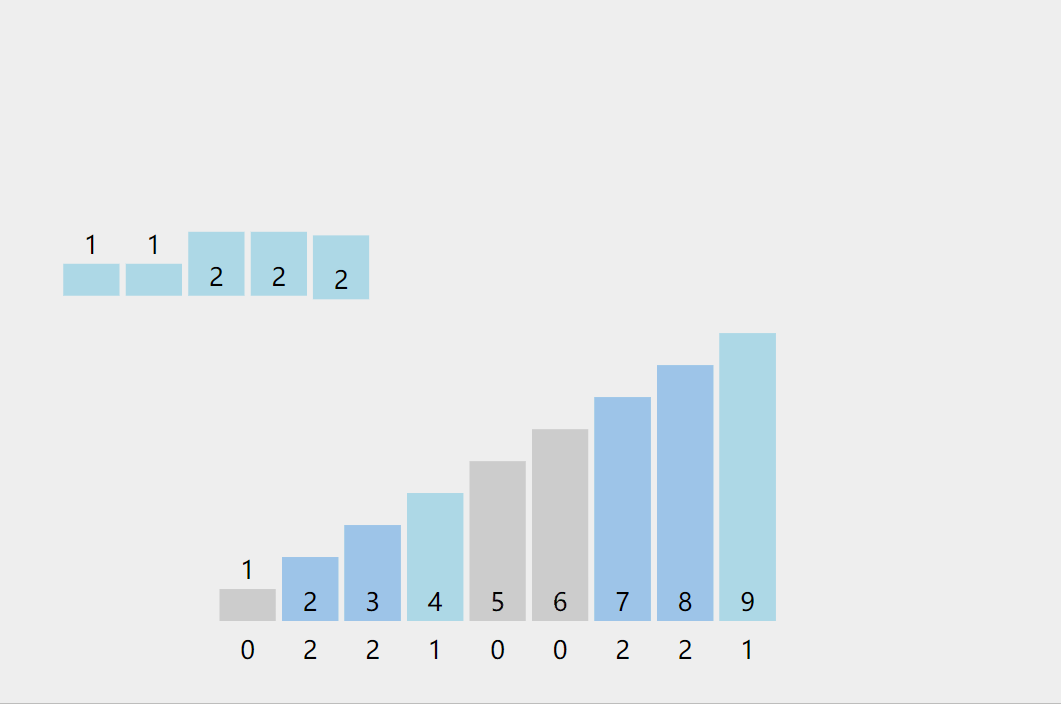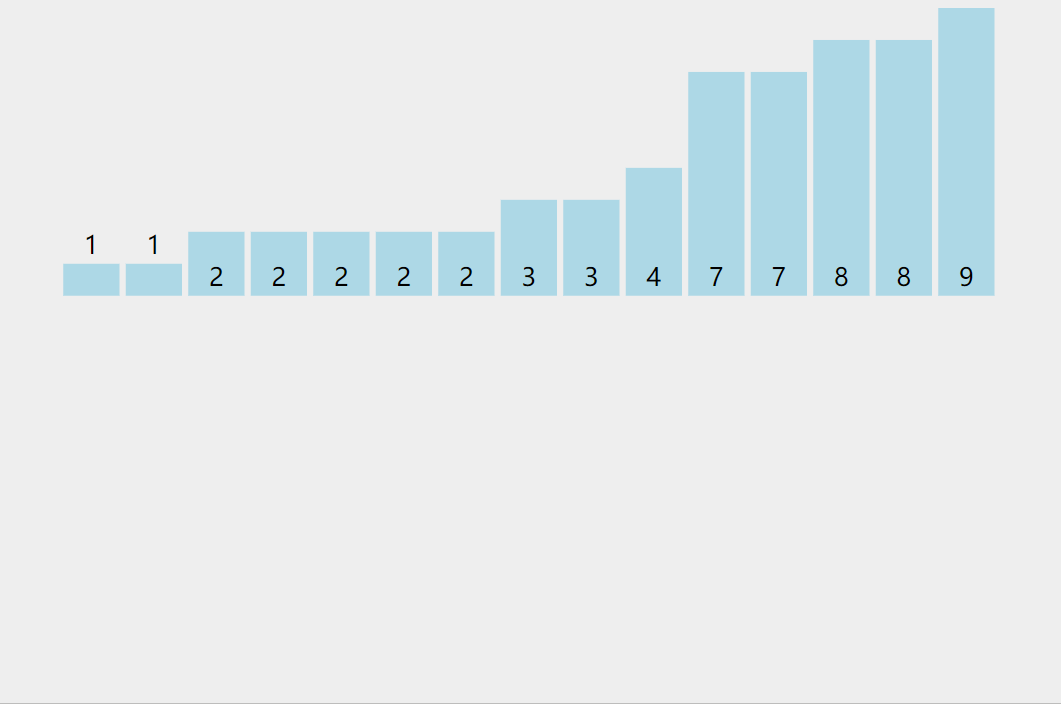
实现代码:
class CountSort {
public static void countSort(int[] array) {
//1. 遍历数组 找到最大值 和 最小值
int max = array[0];
int min = array[0];
//O(N)
for (int i = 1; i < array.length; i++) {
if(array[i] < min) {
min = array[i];
}
if(array[i] > max) {
max = array[i];
}
}
//2. 根据范围 定义计数数组的长度
int len = max - min + 1;
int[] count = new int[len];
//3.遍历数组,在计数数组当中 记录每个数字出现的次数 O(N)
for (int i = 0; i < array.length; i++) {
count[array[i]-min]++;
}
//4.遍历计数数组
int index = 0;// array数组的新的下标 O(范围)
for (int i = 0; i < count.length; i++) {
while (count[i] > 0) {
//这里要加最小值 反应真实的数据
array[index] = i+min;
index++;
count[i]--;
}
}
}
public static void main(String[] args) {
int[] array = new int[]{2,5,1,3,11,0,4,-1,-5,7};
System.out.println("排序前"+ Arrays.toString(array));
countSort(array);
System.out.println("排序后"+ Arrays.toString(array));
}
}
注意:计数排序在排负数时,可将负数的类型转化成 unsigned int。
数组中元素有正有负的情况时不适用计数排序。
计数排序的特性总结:
- 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
- 时间复杂度:O(MAX(N,范围))
- 空间复杂度:O(范围)
- 稳定性:稳定
九、基数排序 (了解)
基数排序是依次根据个位数、十位数、百位数......的大小来排序 ,最终的结果就是排好序的序列
思路:
1.根据所给序列,找到序列中数据的最大值,并求该值的位数。
2.创建十个队列,这里可以将队列形象为桶。根据数据每一位的值放在相应桶中
3.再将桶里面的数据依次取出来
动图如下:

实现代码:
1.时间复杂度O(n)
2.当元素取值范围较大,但元素个数较少时可以利用基数排序
class Soultion_{
public static int countlen(int data){
return (data+"").length();
}
public static int index(int num,int r){
int ret = 0;
for (int i = 1; i <=r ; i++) {
ret = num%10;
num/=10;
}
return ret;
}
public static void sort(int[] array){
int max = array[0];
for (int i = 1; i < array.length ; i++) {
if(array[i]>max)max = array[i];
}
int len = countlen(max);
LinkedList<Integer>[] list = new LinkedList[10];
for (int i = 0; i < list.length; i++) {
list[i] = new LinkedList<>();
}
for (int i = 1; i <=len ; i++) {
for (int j = 0; j < array.length; j++) {
list[index(array[j],i)].offer(array[j]);
}
int k = 0;
for (int j = 0; j < list.length; j++) {
while(!list[j].isEmpty()){
array[k++] = list[j].poll();
}
}
}
}
}
public class RadixSort {
public static void main(String[] args) {
Soultion_ soultion = new Soultion_();
int[] arr = { 23, 1, 4, 9, 98, 132, 42 };
soultion.sort(arr);
System.out.println(Arrays.toString(arr));
}
}十、桶排序 (了解)
桶排序是根据所给序列中数据来划分区间,一个区间就是一个桶,将元素之间差值不大的放进一个桶中。然后对桶内数据进行排序,最后将排好序的桶内数据倒出给原来的数组。
步骤:
1、设置一定数量的空桶
2、遍历待排序序列,将每个元素放入对应桶里
3、对每个不空的桶进行排序
4、从不空的桶将元素从桶中取出
动图如下: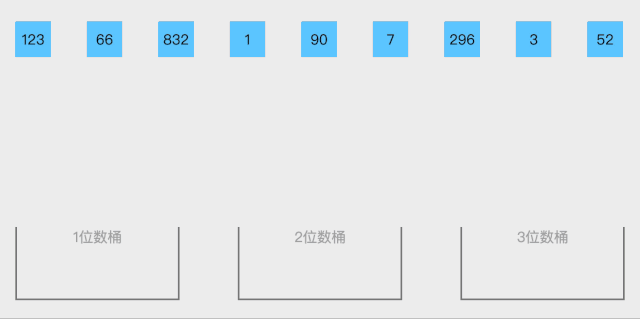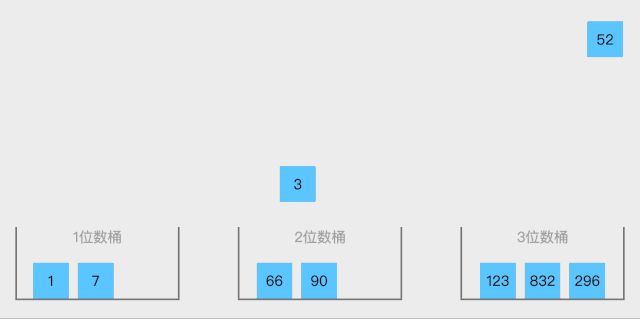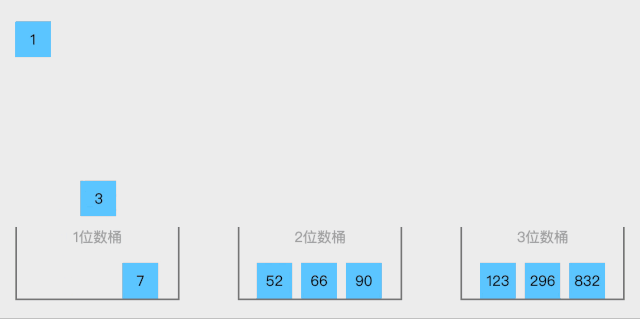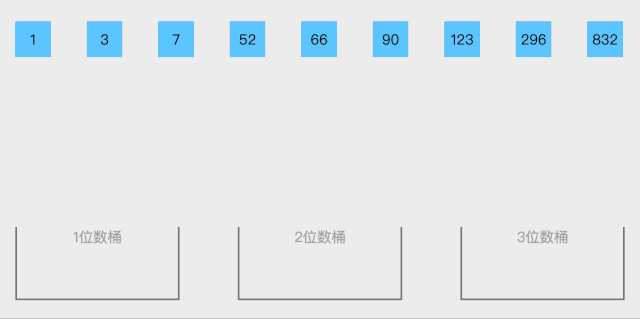
实现代码:
-
时间复杂度:O(N)
-
空间复杂度:O(N+M)
-
稳定性:不稳定
class Sort{
public static void bucketSort(int [] array){
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for (int i = 0; i < array.length; i++) {
max = Math.max(max,array[i]);
min = Math.min(min,array[i]);
}
int reage = (max-min)/ array.length+1;
PriorityQueue<Integer>[] queue = new PriorityQueue[reage];
for (int i = 0; i < reage; i++) {
queue[i] = new PriorityQueue<>();
}
for (int i = 0; i < array.length; i++) {
int num = (array[i]-min)/array.length;
queue[num].offer(array[i]);
}
int k = 0;
for (int i = 0; i < queue.length; i++) {
while(!queue[i].isEmpty()){
array[k++] = queue[i].poll();
}
}
}
}
public class BucketSort {
public static void main(String[] args) {
Sort sort = new Sort();
int[] array = new int[]{3,0,19,15,24,30};
System.out.println("排序前"+ Arrays.toString(array));
sort.bucketSort(array);
System.out.println("排序后"+ Arrays.toString(array));
}
}| 排序方法 | 最好 | 平均 | 最坏 | 空间复杂度 | 稳定性 |
| 冒泡排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 插入排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 希尔排序 | O(n) | O(n^1.3) | O(n^2) | O(1) | 不稳定 |
| 堆排序 | O(n * log(n)) | O(n * log(n)) | O(n * log(n)) | O(1) | 不稳定 |
| 快速排序 | O(n * log(n)) | O(n * log(n)) | O(n^2) | O(log(n)) ~ O(n) | 不稳定 |
| 归并排序 | O(n * log(n)) | O(n * log(n)) | O(n * log(n)) | O(n) | 稳定 |