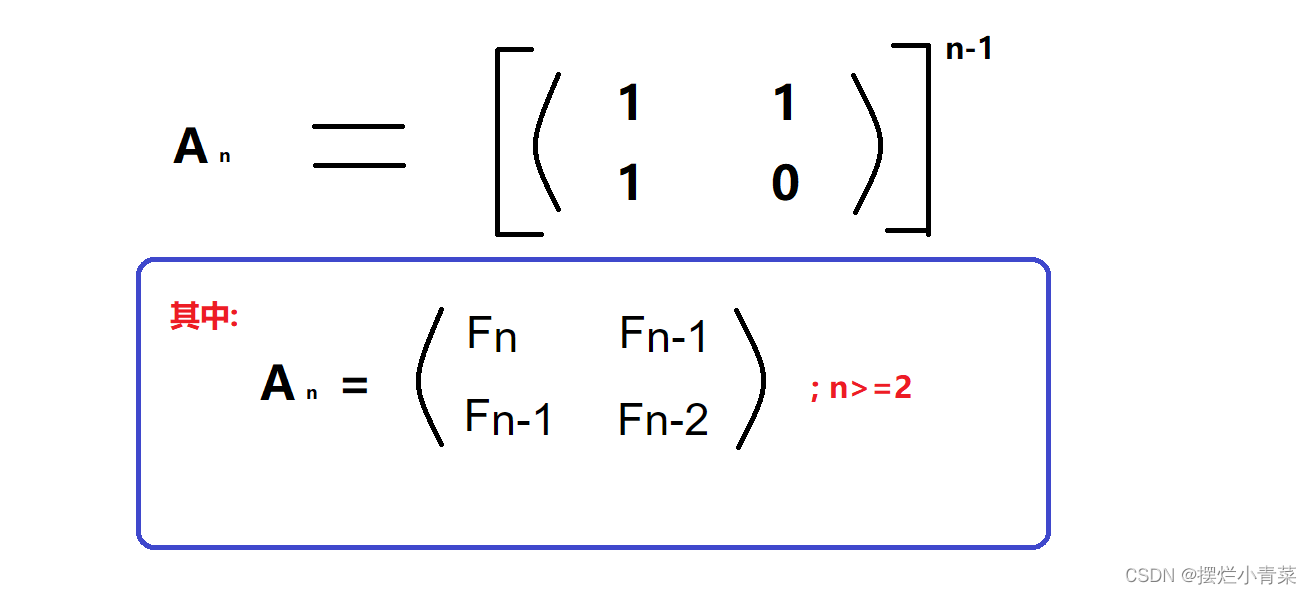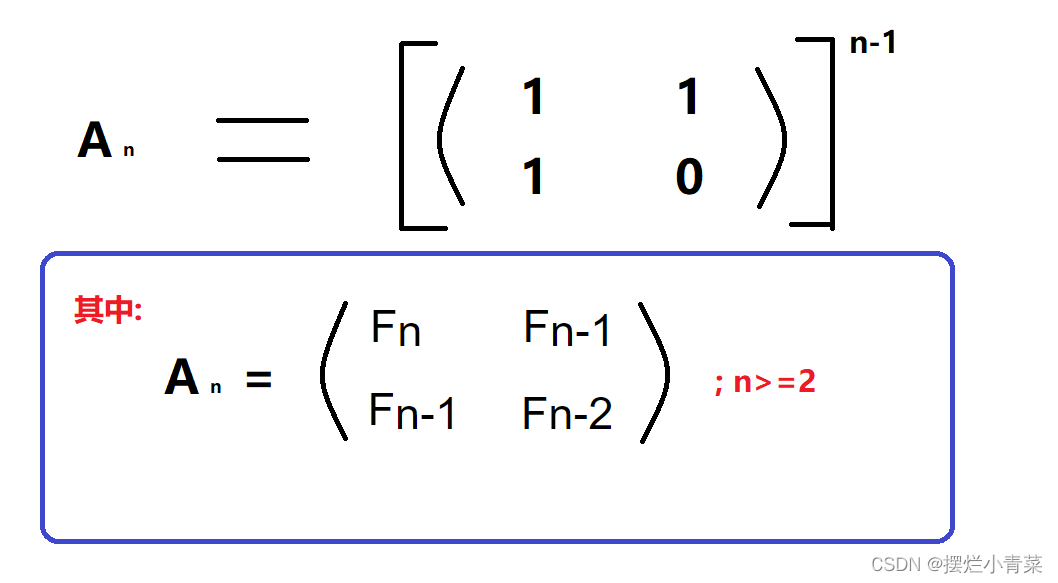目录
一.矩阵乘法与斐波那契数列
1.利用数列的项构造二阶方阵
2.引入矩阵乘法
二.算法实现
1.MatrixFib对象成员变量
2.MatrixFib对象的构造函数
3. MatrixFib对象的成员算法接口
4.对象测试

一.矩阵乘法与斐波那契数列
1.利用数列的项构造二阶方阵
- 😄现定义斐波那契数列:
- 😄再构造二阶方阵An:其中n>=2(我们可以称之为斐波那契方阵)
- 😄当n=2时,A2为下图所示的方阵:
2.引入矩阵乘法
- 😍接下来计算如下矩阵相乘的结果:
- 😍进一步得:
- 😍即:
- 😍于是我们可以得到二阶斐波那契方阵的递推公式:
- 😍通过上面的递推公式我们可以得到斐波那契方阵的通项公式:
- 😍于是通过计算一个特殊的二阶方阵的n-1次方,再取出其中的第一行第一列元素我们就可以得到斐波那契数列的第n项
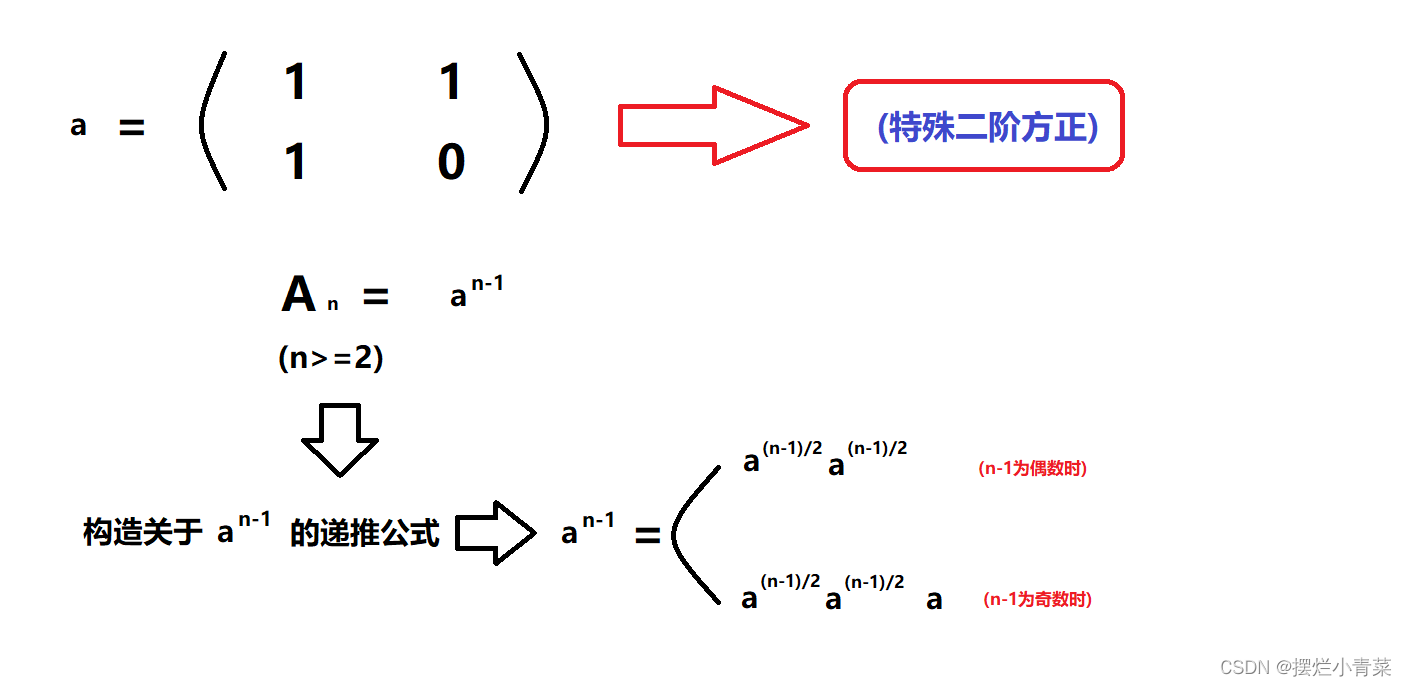
- 😍接着我们记二阶方阵a:
😍再构造关于a的n-1次方的递推公式:
😍基于上述的数学结论,我们可以设计出时间复杂度为O(logN)的算法用于求斐波那契数列的第n项.
二.算法实现
😜我们通过封装一个MatrixFib对象的方式来实现时间复杂度为O(logN)的求斐波那契数列通项算法
😜先给出总体代码:
class MatrixFib { public: //构造函数初始化成员变量 MatrixFib() { _BacMatrix.push_back({ 1,1 }); _BacMatrix.push_back({ 1,0 }); _RetMatrix.push_back({ 1,1}); _RetMatrix.push_back({ 1,0}); _TemMatrix.push_back({ 1,1 }); _TemMatrix.push_back({ 1,0 }); } int Fib(int n) { assert(n >= 0); if (0 == n) { return _BacMatrix[1][1]; } else if (1 == n) { return _BacMatrix[0][1]; } else { return PowerOfMatrix(n-1)[0][0]; } } private: vector<vector<int>>& PowerOfMatrix(int n) { if (1 >= n) { return _BacMatrix; } else if(1 == n%2) { //n为奇数时的递归路径 PowerOfMatrix(n / 2); _RetMatrix = MatrixMul(_RetMatrix,_RetMatrix); _RetMatrix = MatrixMul(_RetMatrix, _BacMatrix); return _RetMatrix; } else { //n为偶数时的递归路径 PowerOfMatrix(n / 2); _RetMatrix = MatrixMul(_RetMatrix, _RetMatrix); return _RetMatrix; } } vector<vector<int>>& MatrixMul(vector<vector<int>>& M1, vector<vector<int>>& M2) { int i = 0; int j = 0; for (i = 0; i < _row; ++i) { for (j = 0; j < _col; ++j) { int sum = 0; for (int k = 0; k < _col; ++k) { sum += M1[i][k] * M2[k][j]; } _TemMatrix[i][j] = sum; } } return _TemMatrix; } private: //二阶方阵的行列数 static const int _row = 2; static const int _col = 2; //用于存储特殊二阶方阵的容器 vector<vector<int>> _BacMatrix; //用于存放特殊二阶方阵的幂的容器 vector<vector<int>> _RetMatrix; //用于临时储存计算结果的容器 vector<vector<int>> _TemMatrix; };
- 😜接下来分模块进行拆解分析
1.MatrixFib对象成员变量
😜MatrixFib对象的成员变量:
class MatrixFib { public: private: //二阶方阵的行列数 static const int _row = 2; static const int _col = 2; //用于存储特殊二阶方阵的容器 vector<vector<int>> _BacMatrix; //用于存放特殊二阶方阵的幂的容器 vector<vector<int>> _RetMatrix; //用于临时储存计算结果的容器 vector<vector<int>> _TemMatrix; };
😜之所以要定义_TemMatrix成员容器是为了能够避免在后续算法接口中出现大量的vector对象之间的深拷贝从而导致算法性能降低(对象传参尽量传引用)
😜所谓特殊二阶方阵:
2.MatrixFib对象的构造函数
//构造函数初始化成员变量 MatrixFib() { _BacMatrix.push_back({ 1,1 }); _BacMatrix.push_back({ 1,0 }); _RetMatrix.push_back({ 1,1}); _RetMatrix.push_back({ 1,0}); _TemMatrix.push_back({ 1,1 }); _TemMatrix.push_back({ 1,0 }); }
- 用该构造函数实现MatrixFib对象的成员变量初始化
3. MatrixFib对象的成员算法接口
- 😜求二阶方阵M1和M2乘积的私有成员接口:
vector<vector<int>>& MatrixMul(vector<vector<int>>& M1, vector<vector<int>>& M2) { int i = 0; int j = 0; for (i = 0; i < _row; ++i) { for (j = 0; j < _col; ++j) { int sum = 0; for (int k = 0; k < _col; ++k) { sum += M1[i][k] * M2[k][j]; } _TemMatrix[i][j] = sum; } } return _TemMatrix; }😜_TemMatrix是成员容器,用来暂时存放两个方阵相乘的结果
😜根据之前的数学推导,我们接下来需要设计一个求特殊二阶方阵n次幂的成员接口:
😜根据上面的递推公式我们可以在O(logN)的时间复杂度下实现这个私有成员接口:
vector<vector<int>>& PowerOfMatrix(int n) { if (1 >= n) { return _BacMatrix; } else if(1 == n%2) { //n为奇数时的递归路径 PowerOfMatrix(n / 2); _RetMatrix = MatrixMul(_RetMatrix,_RetMatrix); _RetMatrix = MatrixMul(_RetMatrix, _BacMatrix); return _RetMatrix; } else { //n为偶数时的递归路径 PowerOfMatrix(n / 2); _RetMatrix = MatrixMul(_RetMatrix, _RetMatrix); return _RetMatrix; } }😜注意_RetMatrix,_BacMatrix都是类的成员容器
😜最后再提供一个public的Fib成员接口,使得外界可以调用它来求斐波那契数列的第n项:
int Fib(int n) { assert(n >= 0); if (0 == n) { return _BacMatrix[1][1]; } else if (1 == n) { return _BacMatrix[0][1]; } else { return PowerOfMatrix(n-1)[0][0]; } }😜注意PowerOfMatrix接口返回的是容器的引用
4.对象测试
剑指 Offer 10- II. 青蛙跳台阶问题 - 力扣(Leetcode)
https://leetcode.cn/problems/qing-wa-tiao-tai-jie-wen-ti-lcof/solutions/2241390/yong-fei-bo-na-qi-er-jie-fang-zhen-shi-x-z7hg/
😜将MatrixFib对象稍作修改就可以用于题解测试
😜题解代码:
class Solution { public: //构造函数初始化成员变量 Solution() { _initMatrix.push_back({ 2,1 }); _initMatrix.push_back({ 1,1 }); _BacMatrix.push_back({ 1,1 }); _BacMatrix.push_back({ 1,0 }); _RetMatrix.push_back({ 1,1}); _RetMatrix.push_back({ 1,0}); _TemMatrix.push_back({ 1,1 }); _TemMatrix.push_back({ 1,0 }); } //求斐波那契数列第n项的公共接口 int numWays(int n) { assert(n >= 0); if (0 == n) { return _initMatrix[1][1]; } else if (1 == n) { return _initMatrix[1][1]; } else if(2 == n) { return _initMatrix[0][0]; } else { return MatrixMul(PowerOfMatrix(n - 2), _initMatrix)[0][0]; } } //求特殊二阶方阵的n次幂的递归接口 vector<vector<unsigned long long>>& PowerOfMatrix(int n) { if (1 >= n) { return _BacMatrix; } else if(1 == n%2) { PowerOfMatrix(n / 2); _RetMatrix = MatrixMul(_RetMatrix,_RetMatrix); _RetMatrix = MatrixMul(_RetMatrix, _BacMatrix); return _RetMatrix; } else { PowerOfMatrix(n / 2); _RetMatrix = MatrixMul(_RetMatrix, _RetMatrix); return _RetMatrix; } } //计算两个矩阵相乘结果的接口 vector<vector<unsigned long long>>& MatrixMul (vector<vector<unsigned long long>>& M1 ,vector<vector<unsigned long long>>& M2) { int i = 0; int j = 0; for (i = 0; i < _row; ++i) { for (j = 0; j < _col; ++j) { unsigned long long sum = 0; for (int k = 0; k < _col; ++k) { sum += M1[i][k] * M2[k][j]; } _TemMatrix[i][j] = sum%1000000007; } } return _TemMatrix; } private: //二阶方阵的行列数 static const int _row = 2; static const int _col = 2; //用于存储特殊二阶方阵 vector<vector<unsigned long long>> _BacMatrix; //用于存储由F2,F1,F0构成的二阶方阵 vector<vector<unsigned long long>> _initMatrix; //用于存储Fn,Fn-1,Fn-1,Fn-2构成的二阶方阵 vector<vector<unsigned long long>> _RetMatrix; //用于存储矩阵相乘的临时计算结果 vector<vector<unsigned long long>> _TemMatrix; };