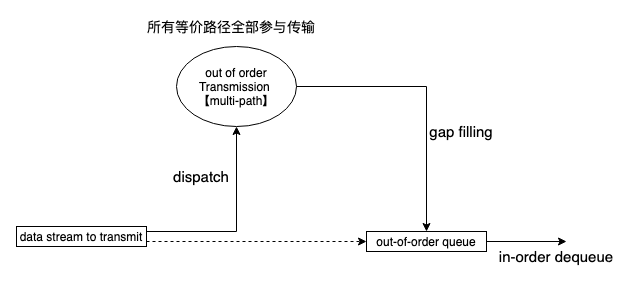
文章摘录链接
1.树基本概念
计算机数据结构中的树就是对显示中的树的一种抽象(倒置现实中的树)。
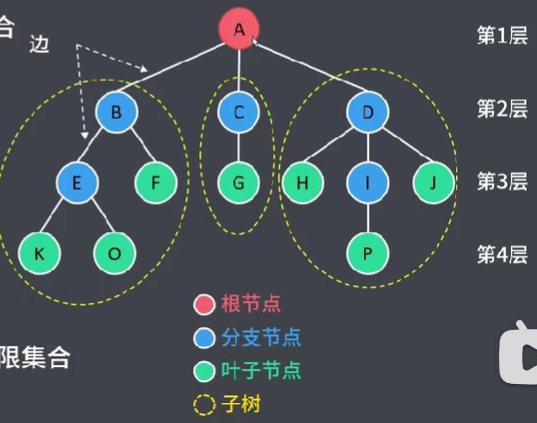
1.1 树
有层次关系N(N≥0)个节点的有限集合
空树: N=0
非空树: 有且只有一个根节点
1.2 节点
根节点
分支节点
叶子节点
前驱(父节点)
后继(子节点)
1.3 子树
除根外,可分为m个互不相交的有限集合
1.4 边
1.5 度
1.6 高度(深度、层次)
1.7 有序数/无序树
各节点的子树从左至右有/无次序。
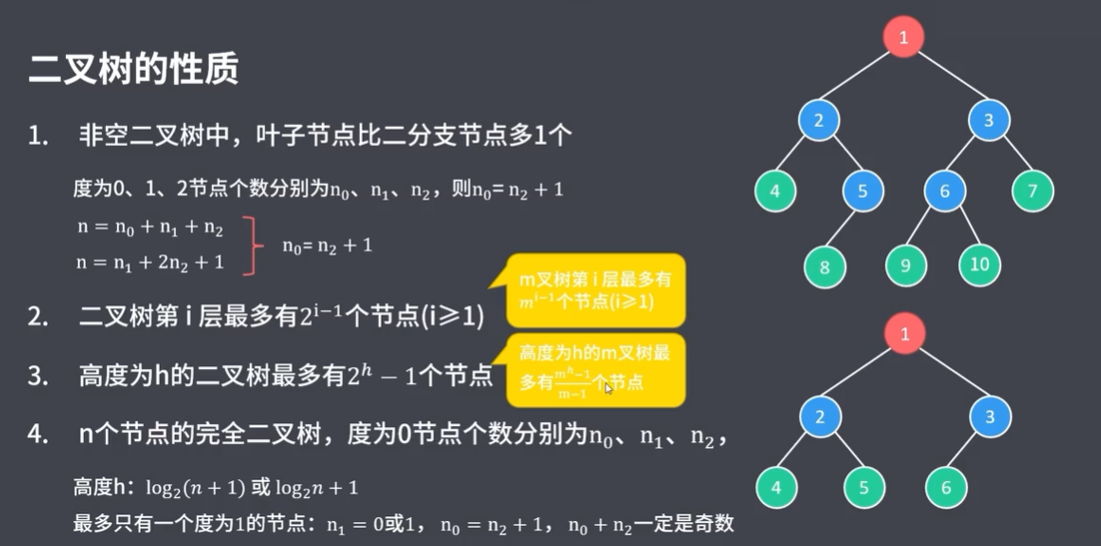
2.树的性质
1
节点 = 总度数 + 1
节点的度 = 节点孩子(分支)个数
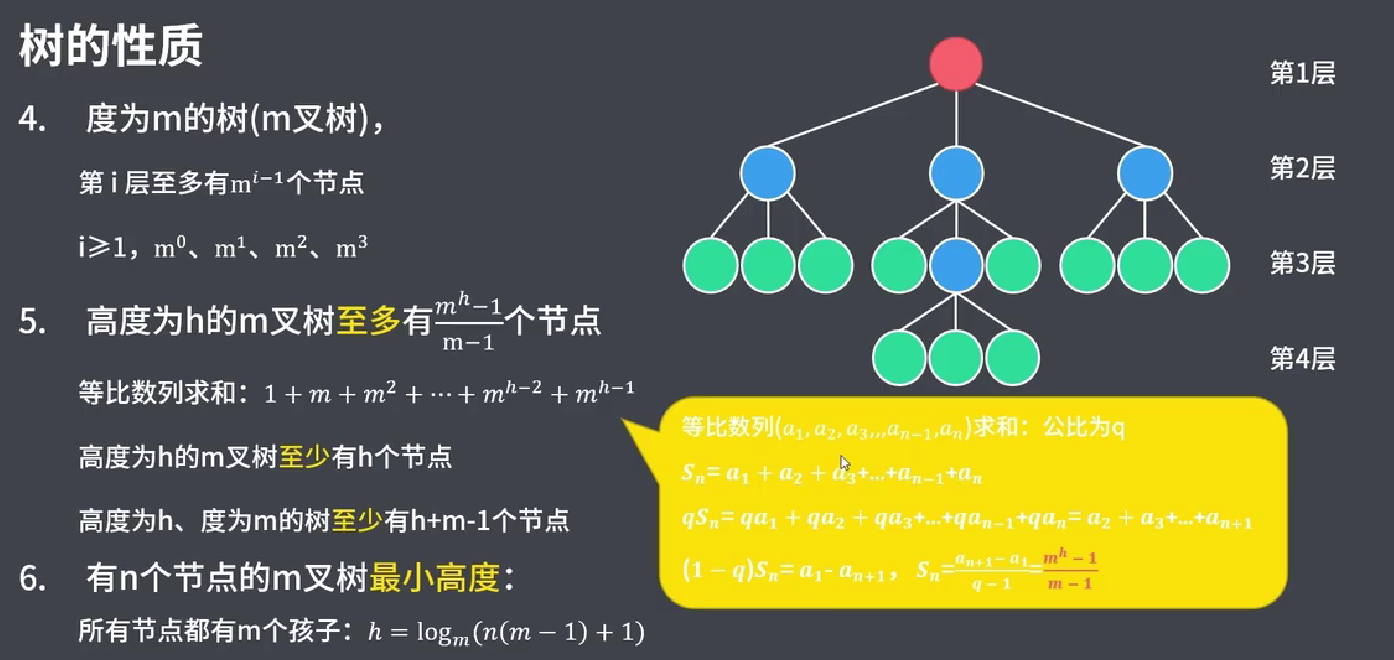
2
度为m的树:各节点度的最大值为m
任意节点的度 ≤ m
至少一个节点的度 = m
3
m叉树的区别:每个节点最多有m个孩子
任意节点的度 ≤ m
允许所有节点的度都 < m
2.树的存储结构
顺序存储对应的就是数组。
链式存储对应的就是链表。
再复杂的数据结构,要么是数组存储,要么是链表存储,再么是数组+链表存储。
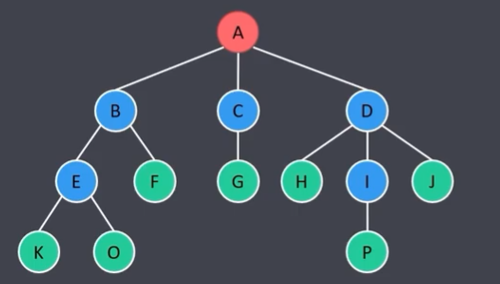
2.1树的双亲表示法(顺序存储)
优点:可以快速找到某节点的父节点
缺点:无法快速找到某节点的子节点

2.2 树的孩子表示法(顺序存储 + 链式存储)
实际应用:hashmap

2.3 树的孩子兄弟表示法(链式存储)

3.森林
森林是m(m>0)颗 互不相交 树的集合
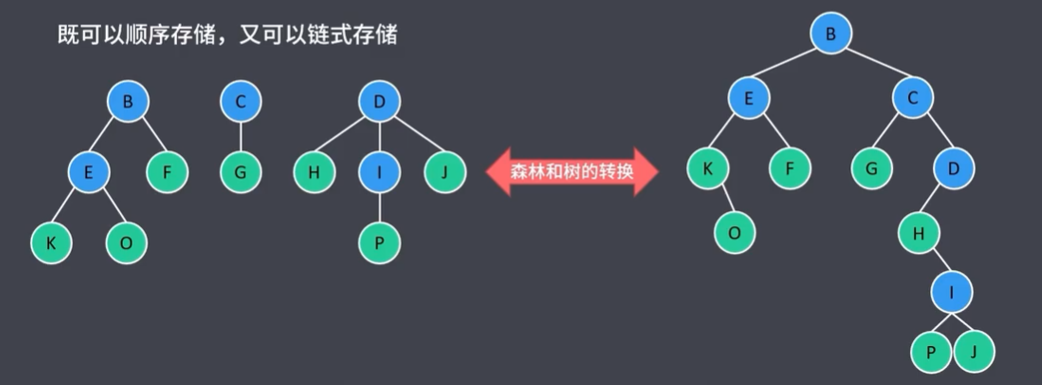
既可以顺序存储,又可以链式存储。
森林和二叉树转换:
森林根节点间是兄弟。
4.二叉树
4.1 二叉树定义
Binary Tree.
节点的度 ≤ 2 的有序数。 `二叉树必须是有序的`。
空树、只有根节点的树、只有左子树、只有右子树、左右子树都有
4.2 二叉树分类
4.2.1 满二叉树
每一层都铺满,只有最后一层是叶子结点。
高为h,节点数 2^h - 1 。(原来m叉树公式带入而来:(m^h-1)/(m-1) )
只有最后一层有叶子结点
不存在度为1的节点
按层序从1编号,i的左子为2i,右子为2i+1,父为i/2
4.2.2 完全二叉树
从上往下,从左至右。
可以理解为满二叉树去掉最下层右边部分叶子结点的树。
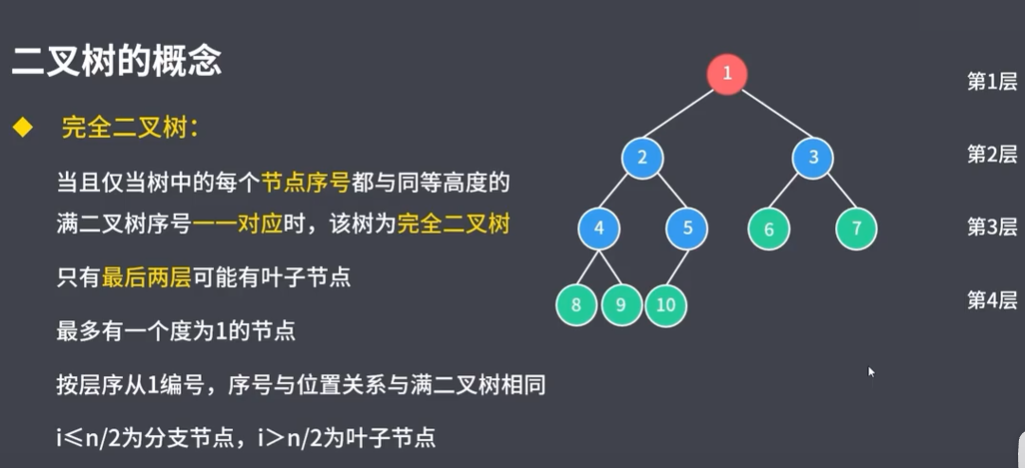
4.2.3 二叉排序树
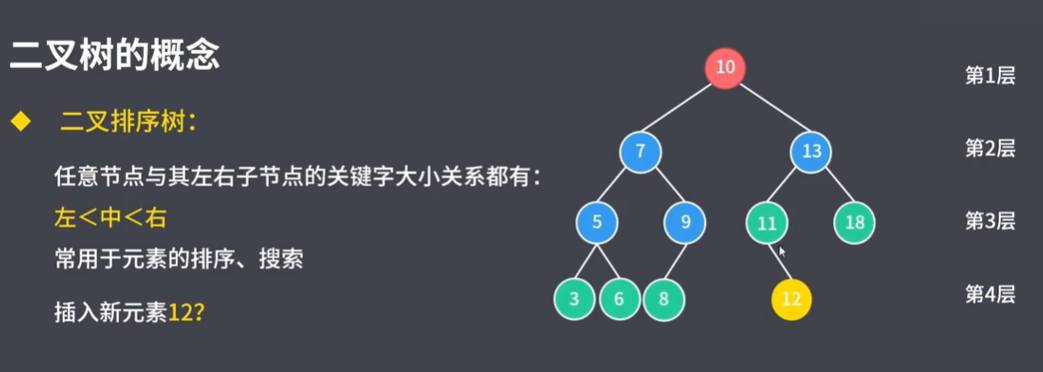
4.2.4 平衡二叉树
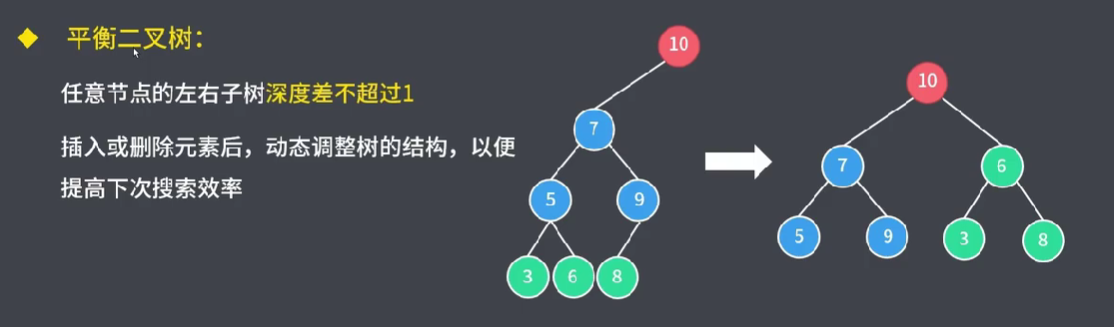
4.3 二叉树的存储结构
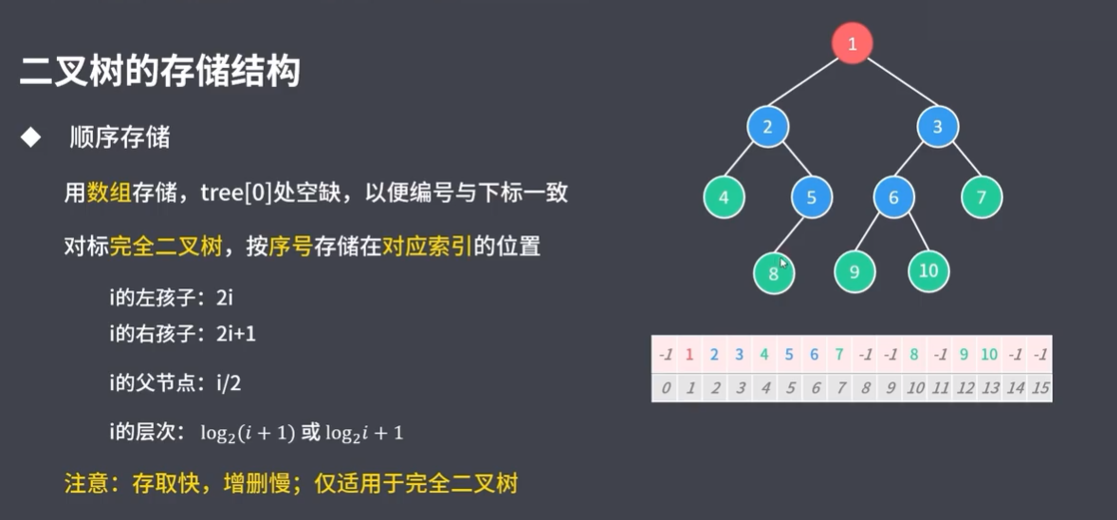
4.3.1 顺序存储
是将普通的二叉树当成完全二叉树来存的。并不是说只有完全二叉树才能顺序存储。
4.3.2 链式存储
默认删除步骤:
将右侧子节点替换要删除的节点,次之 左侧子节点替换。

5.如何访问二叉树
5.1 二叉树的遍历
5.1.1 先序遍历
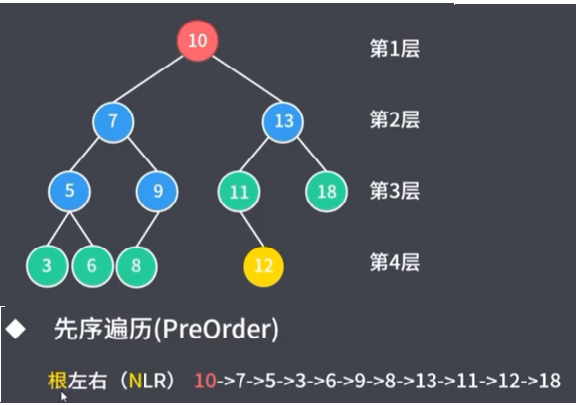
5.1.2 中序遍历
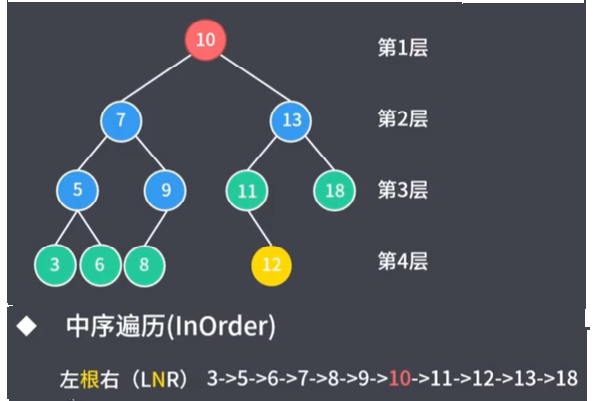
5.1.3 后序遍历
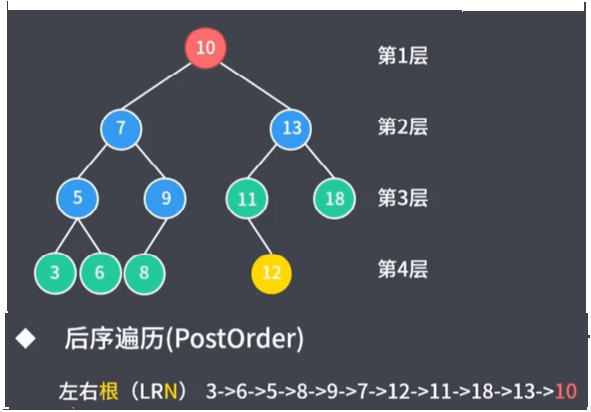
5.1.4 层次遍历
利用先进先出队列。
5.2 线索二叉树
通过优化存储结构,增加前、中、后序遍历速度。不包含层次遍历。
线索化是指针对某一种遍历方式进行线索化,而不是针对二叉树进行线索化。
同一个二叉树,由于使用的遍历方式不同得到的线索二叉树是不同的。
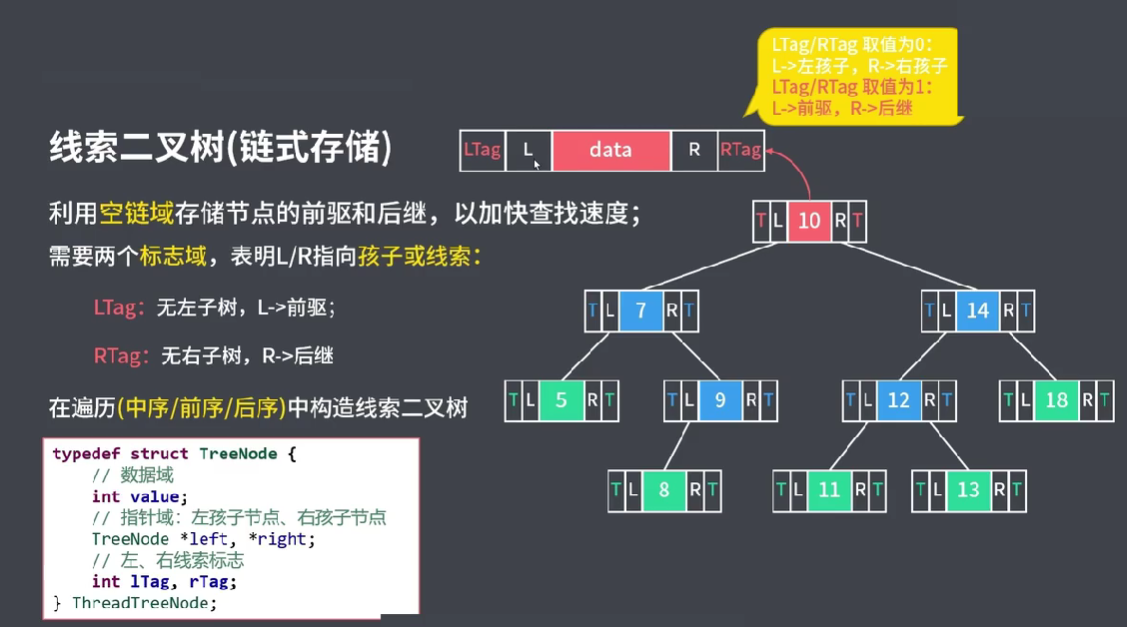
5.2.1 前序遍历
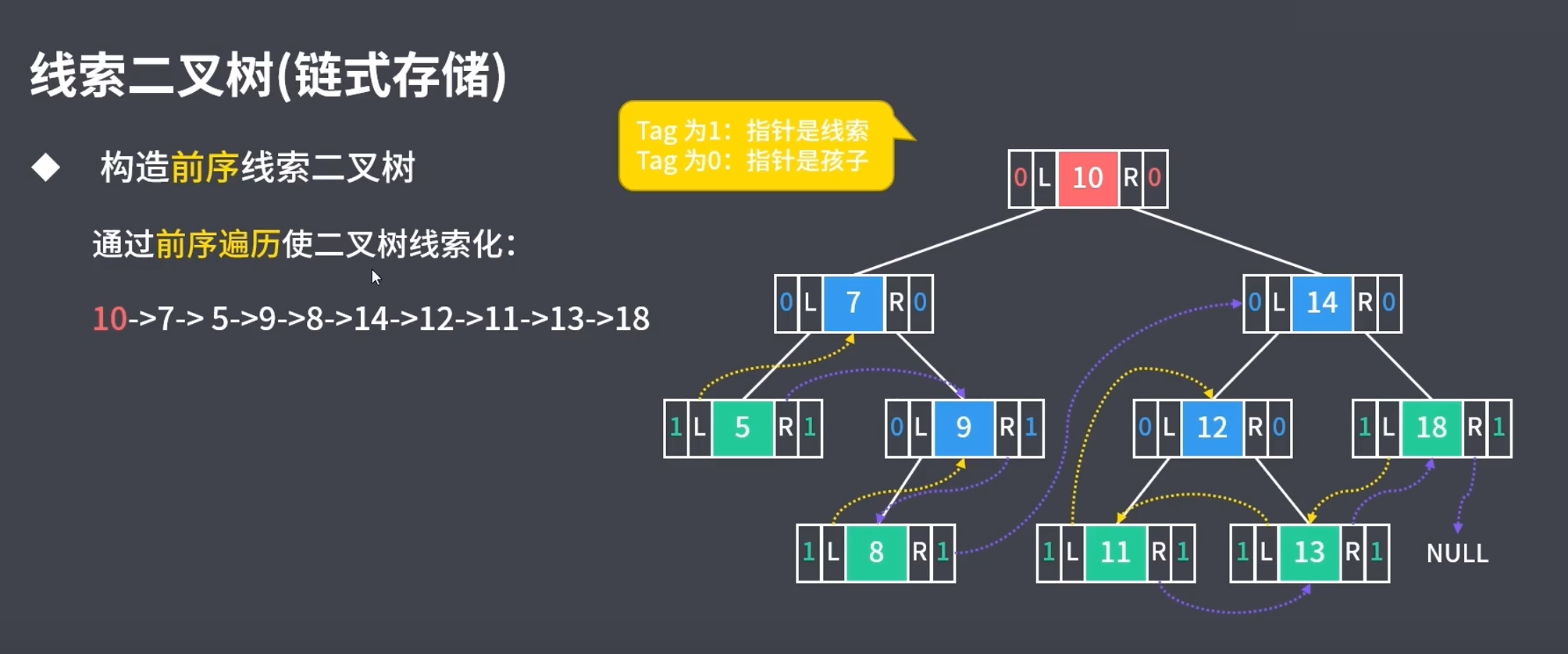
5.2.2 中序遍历
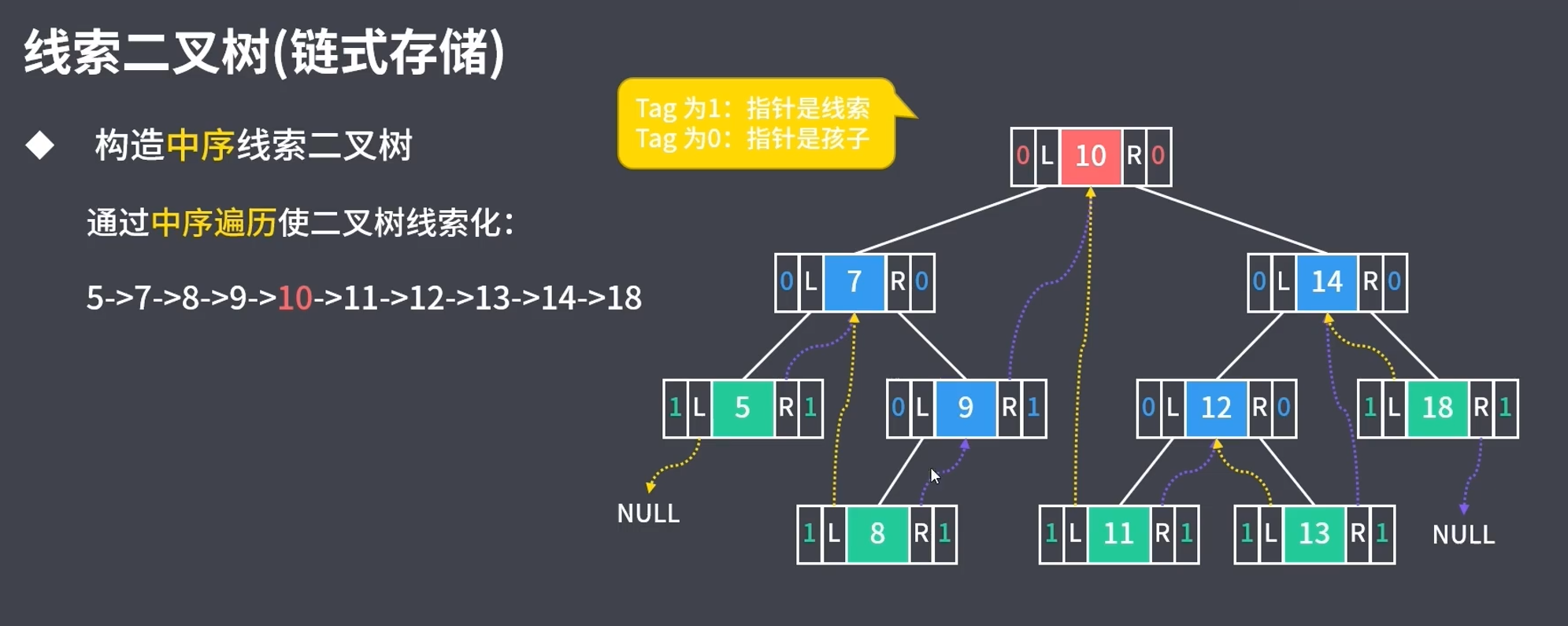
5.2.3 后序遍历
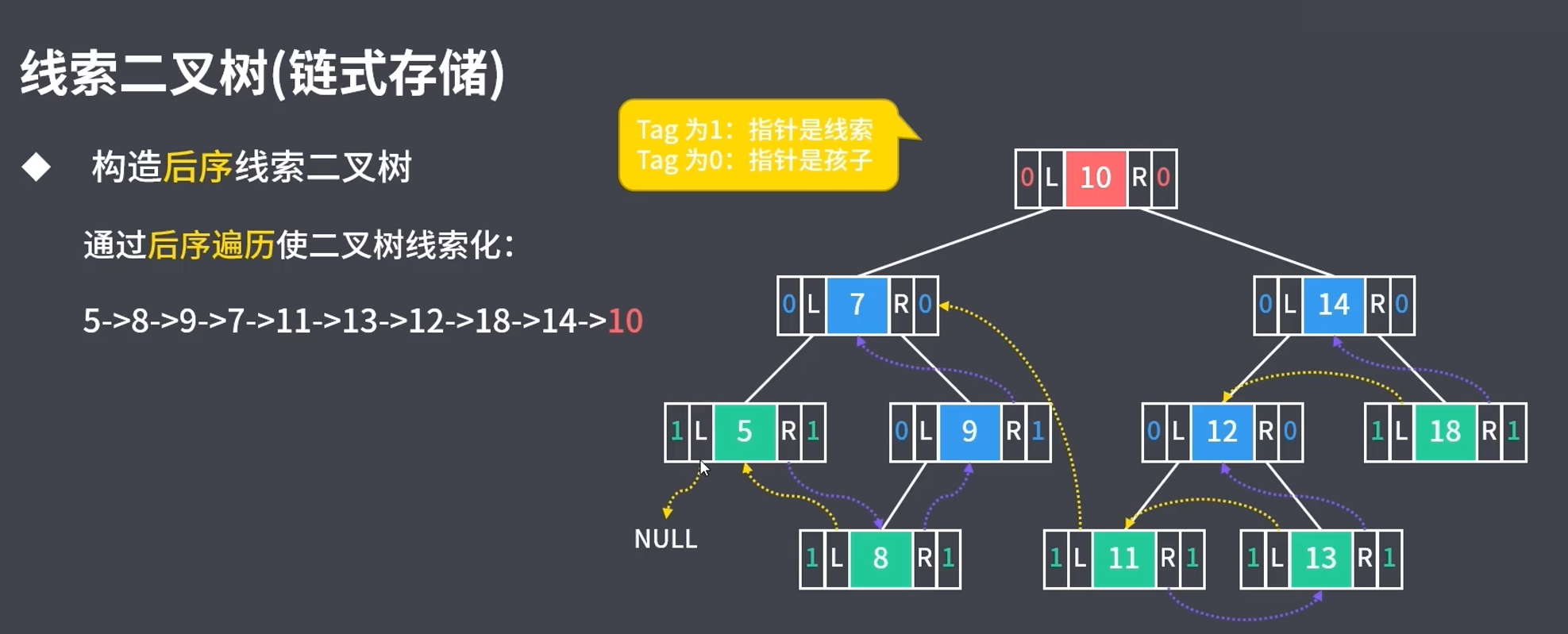
6.二叉树应用场景
6.1 二叉查找树(BST)
6.1.1 概念
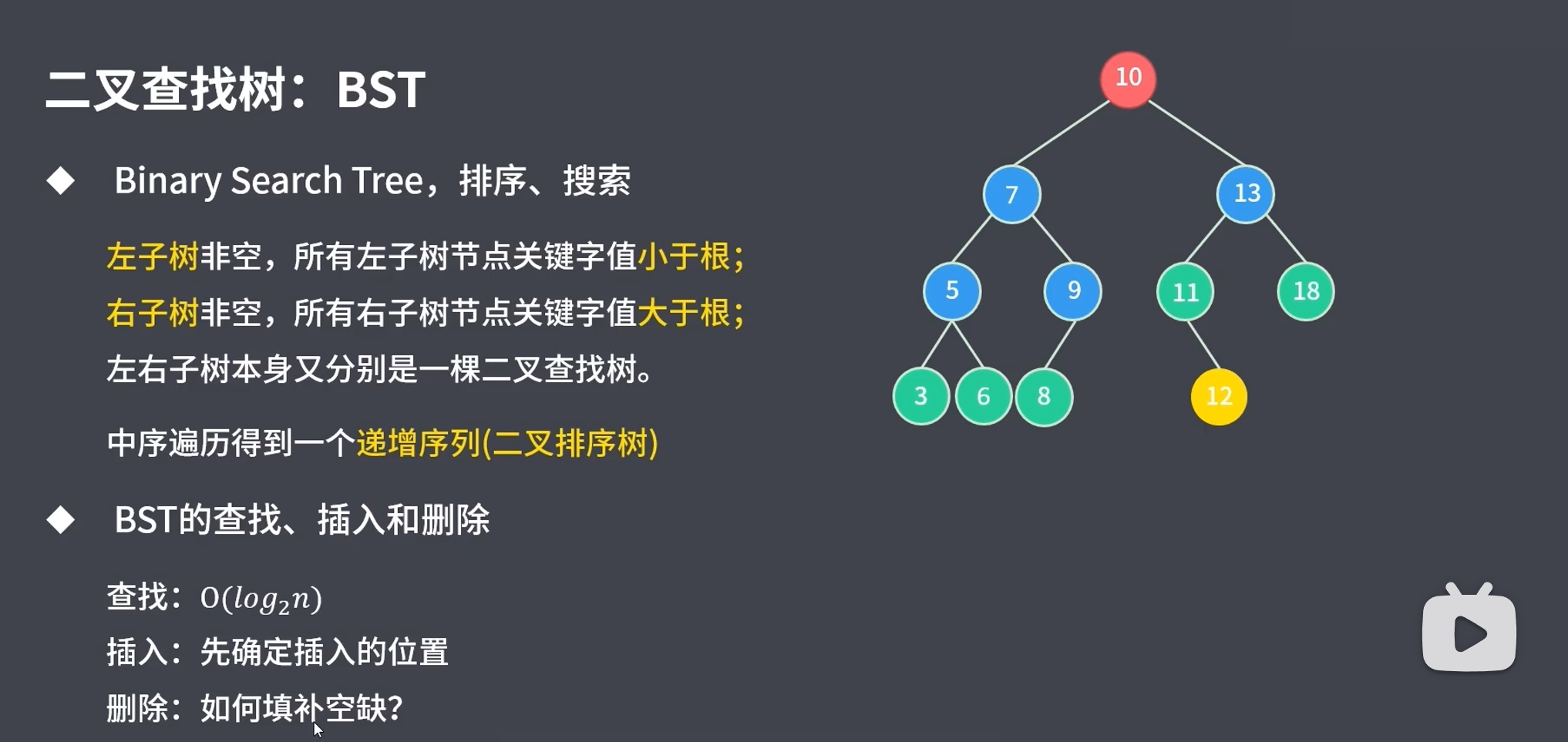
6.1.2 BST查找
因为BST的概念,查找只会往一个子树的方向查找,故时间复杂度就是层次高度。即O(log2n).
6.1.3 BST插入
先进行查找,确定插入位置。
插入的时间复杂度 = 查找插入位置 + 插入时间复杂度1 = O(log2n)
6.1.4 BST删除
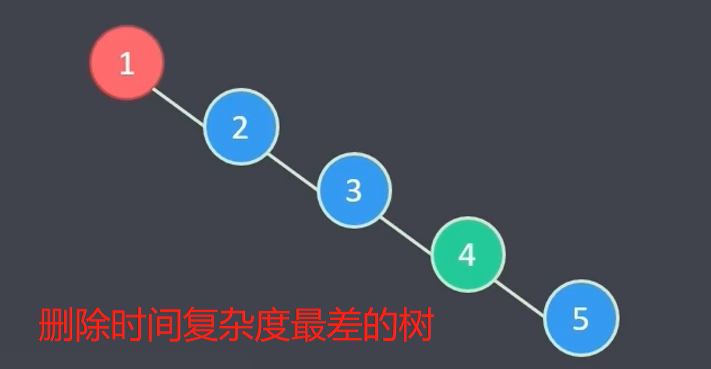
时间复杂度(平均) = 查找插入位置 + 循环查找插入位置 = mO(log2n) = O(log2n)
时间复杂度(最差,当树是个单节点链接链表时)= O(n)
分三种情况:
1.删除度为0的节点
直接删掉
2.删除度为1的节点
将该节点的前驱或后继直接连到该节点所在的位置即可。
3.删除度为2的节点
简单情况:要删除的几点前驱或后继节点的度为0,以按照删除度为1的节点的思路进行节点位置的调整。
复杂情况:要删除的节点前驱或后继节点的前驱或后继为1或2,思路一样,但需要递归待替换的节点。
6.2 平衡二叉树(AVL)
首先是一个二叉查找树(BST),并增加了平衡要求。
应用实例:hashmap
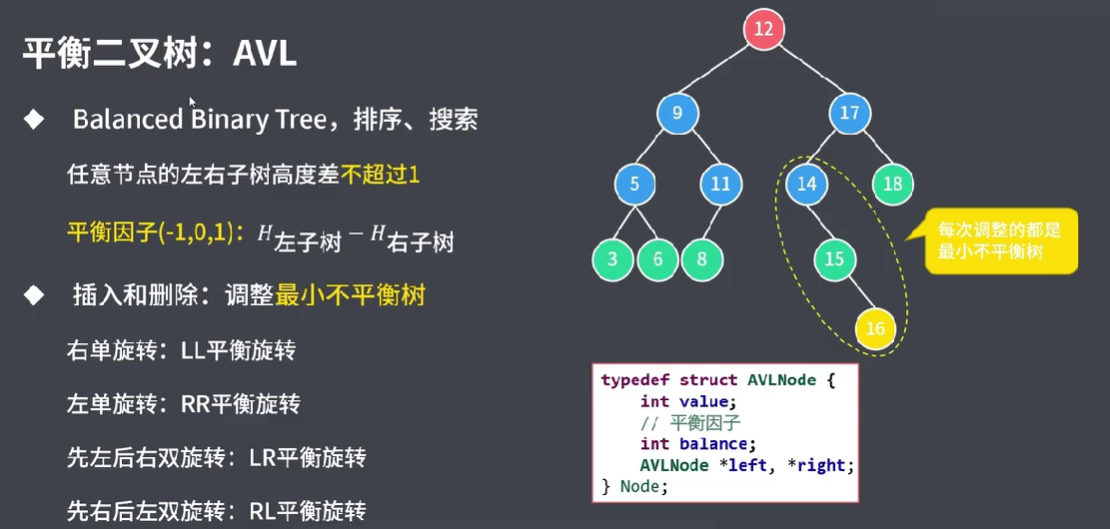
注意:
AVL进行插入或删除会导致失衡,那么相应的引出调整失衡(即旋转)的概念。
调整的应是最小不平衡二叉树。
6.2.1 失衡情况(4种)
旋转名字中的方向(如,左单、右单)指的是物理旋转的方向,可根据下面的实例看出来。
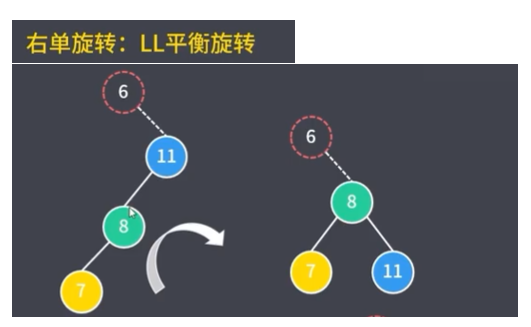
6.2.1.1 右单旋转(LL平衡旋转)
此种旋转适用于在当前节点的左孩子节点(第一个L)的左子树(第二个L)进行插入的情况。
注意:
旋转,挪节点时都以二叉查找树(BST)为前提。
例:如下图,
当前节点11的左孩子节点的左子树插入节点7.
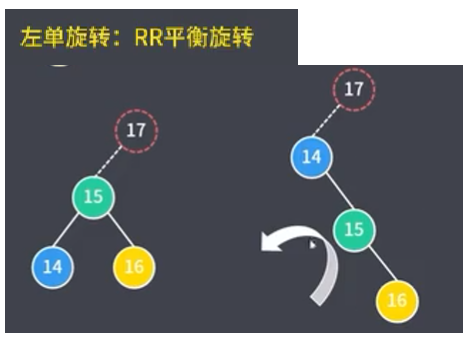
6.2.1.2 左单旋转(RR平衡旋转)
此种旋转适用于在当前节点的右孩子节点(第一个R)的右子树(第二个R)进行插入的情况。
注意:
旋转,挪节点时都以二叉查找树(BST)为前提。
例:如下图,
当前节点14的右孩子节点的右子树插入节点16.
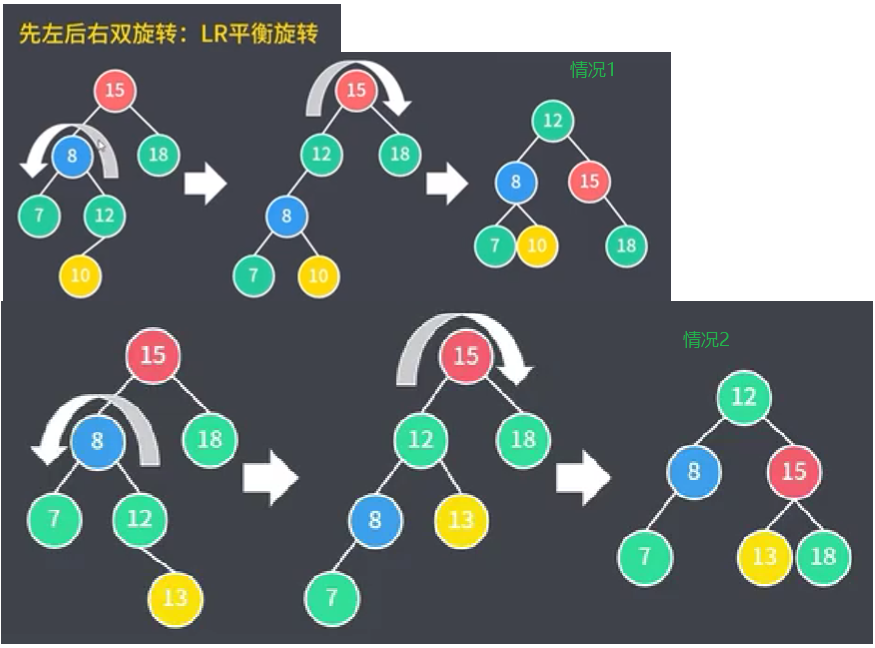
6.2.1.3 先左后右双旋转(LR平衡旋转)
需要先进行一次左旋转,再进行一次右旋转。
此种旋转适用于在当前节点的左孩子节点(第一个L)的右子树(第二个R)进行插入节点的情况,
以上概念为前提,又分为在该右子树下插入左节点和右节点两种情况。
注意:
两次旋转,挪节点时都以二叉查找树(BST)为前提。
例:如下图,
情况1:当前节点15的左孩子节点的右子树插入左节点10.
情况2:当前节点15的左孩子节点的右子树插入右节点13.
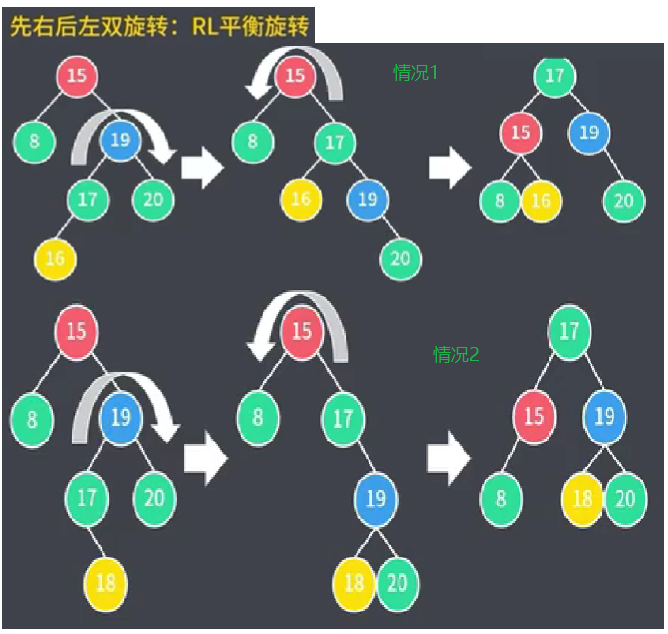
6.2.1.4 先右后左双旋转(RL平衡旋转)
需要先进行一次右旋转,再进行一次左旋转。
此种旋转适用于在当前节点的右孩子节点(第一个R)的左子树(第二个L)进行插入节点的情况,
以上概念为前提,又分为在该右子树下插入左节点和右节点两种情况。
注意:
两次旋转,挪节点时都以二叉查找树(BST)为前提。
例:如下图,
情况1:当前节点15的右孩子节点的左子树插入左节点16.
情况2:当前节点15的右孩子节点的左子树插入右节点18.
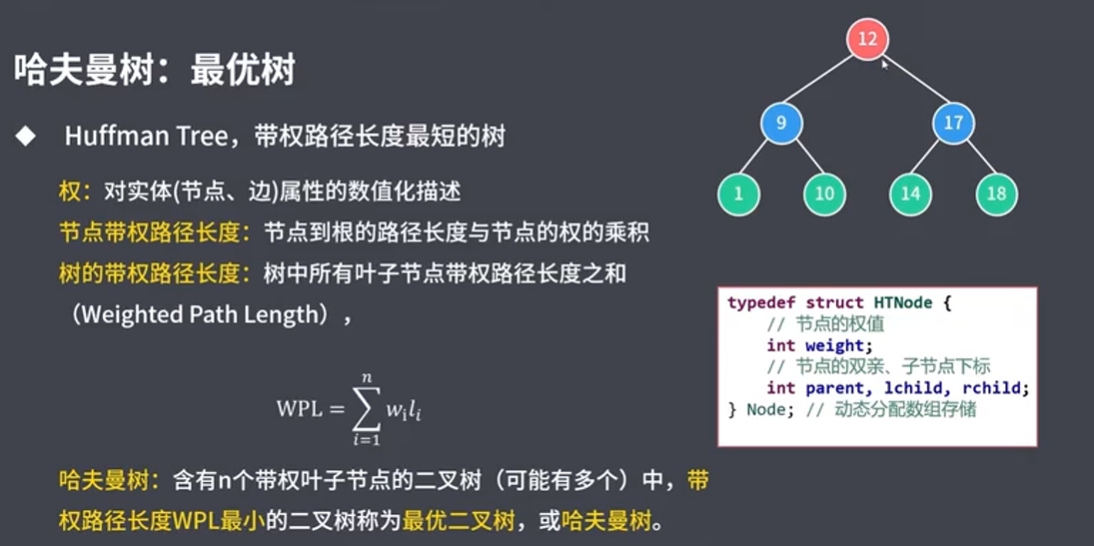
6.3 哈夫曼树
哈夫曼树中没有度为1的节点。
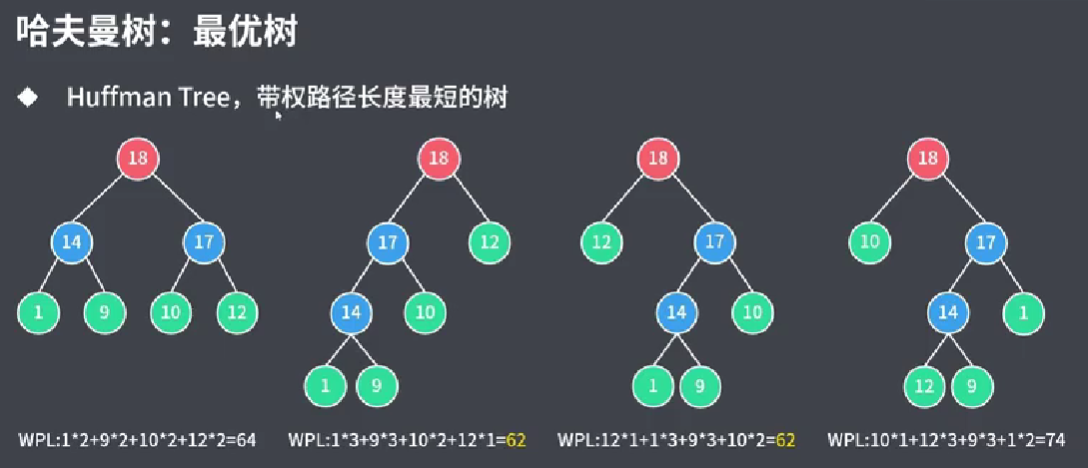
哈夫曼树不只有一个,如下图所示
6.3.1 哈夫曼树的构造
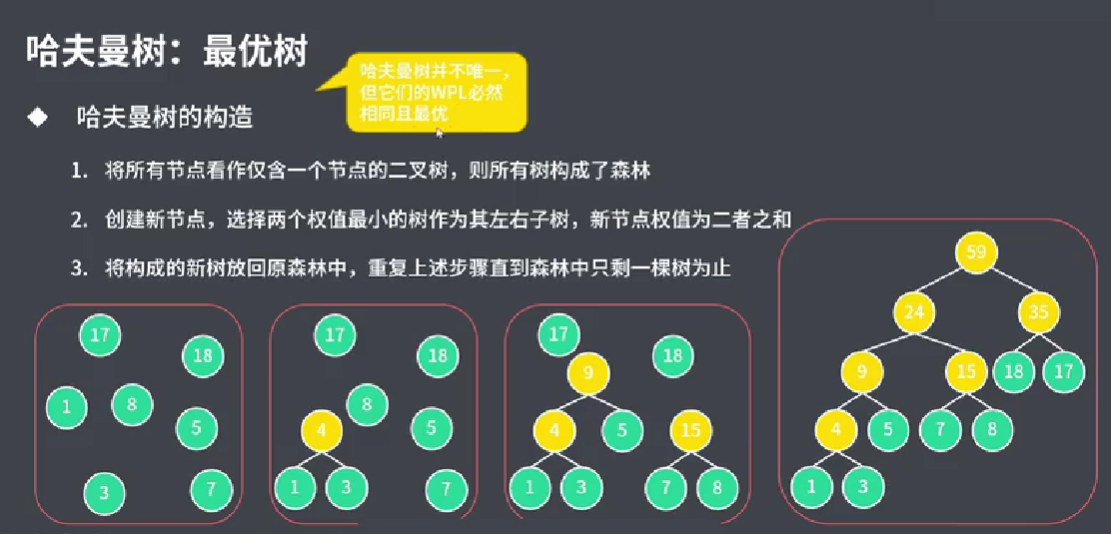
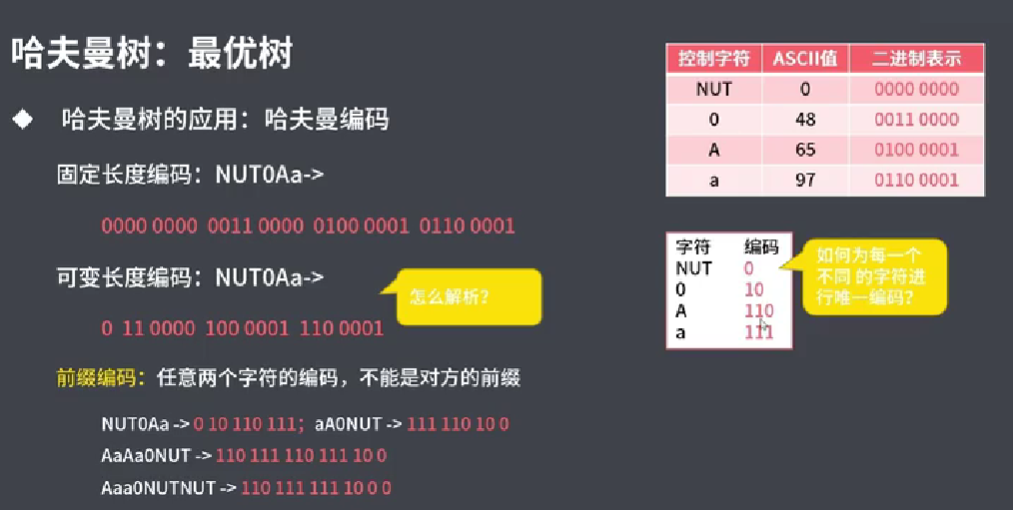
6.3.2 哈夫曼树的应用–哈弗曼编码
计算机间传递数据以二进制流进行,若采取固定长度编码,则会浪费空间。
进而衍生出可变长度编码,但解码会有问题。
最后衍生出前缀编码,
最后利用哈夫曼树得到字符的前缀,最终得到哈弗曼编码。
最终叶子节点带权路径总长度之和就是电文的长度。

7.树了解流程
参考链接
树 -> 二叉树 -> 满二叉树 -> 完全二叉树 -> 二叉查找树(Binary Search Tree - BST,又称二叉排序树、二叉搜索树) -> 平衡二叉搜索树 (Balanced binary search trees,又称AVL树、平衡二叉查找树) -> 红黑树(Red - Black Tree,一种自平衡二叉搜索树(BST)) -> B-Tree(B树) -> B+ Tree(B+树)
7.1 红黑树
红黑树,Red-Black Tree 「RBT」是一个自平衡(不是绝对的平衡)的二叉查找树(BST)