KuiperInfer深度学习推理框架-源码阅读和二次开发(2)：算子开发流程(以sigmoid为例)

前言：KuiperInfer是一个从零实现一个高性能的深度学习推理库，中文教程已经非常完善了。本系列博客主要是自己学习的一点笔记和二次开发的教程，欢迎更多的AI推理爱好者一起来玩。这篇写一下算子开发流程，以sigmoid算子为例，为下一节我们自己手写算子打下基础。

sigmoid算子原理

预处理指令#pragma

OpenMP并行处理

OpenMP简介

#pragma omp parallel for num_threads()

编译 -fopenmp选项

算子开发模板

explicit修饰构造函数

重载函数 Forward()

单例模式 GetInstance()

测试文件

NCNN实现借鉴

参考

sigmoid算子原理

在写算子之前需要对算子的功能非常熟悉，选取这个算子讲解的原因有两个：

1、深度学习中最常用的激活函数之一。

2、公式非常简单：

具体来说有如下特点：

神经网络中的激活函数, 其作用就是引入非线性;
输出范围有限, 数据在传递的过程中不容易发散; 缺点是饱和的时候梯度太小;
输出范围为(0, 1), 所以可以用作输出层, 输出表示概率;
容易求导, y'=y(1-y), 这样很容易做bp(back propagation, 反向传播).

预处理指令#pragma

C程序在整个编译过程中要经过一下这几步：

步骤	过程	指令
预处理	展开头文件/宏替换/去掉注释/条件编译	（test.i main .i）
编译	检查语法，生成汇编	（ test.s main .s）
汇编	汇编代码转换机器码	(test.o main.o)
链接	链接到一起生成可执行程序	a.out

在C/C++中共有以下预处理指令：

pragma便是预处理指令的一种，这条指令时用来制定不同的编译器选项。这些选项根据平台和所使用的编译器各有不同。查询你所使用的编译器的手册或者参考文件，找到你能使用#pragma定义的参数的信息。

如果编译器不支持#pragma里面的参数，那么就会忽略这条命令，不会产生任何语法错误。

OpenMP并行处理

kuiper中#pragma只使用了#pragma omp parallel，这是一个并行操作。其他的指令后面遇到后再学习吧，先学习这一个。

OpenMP简介

OpenMP 是由 OpenMP Architecture Review Board 牵头提出的，并已被广泛接受的，用于共享内存并行系统的多线程程序设计的一套编译指令 (Compiler Directive)。OpenMP 支持的编程语言包括 C 语言、C++ 和 Fortran；而支持 OpenMP 的编译器包括 Sun Compiler，GNU Compiler 和 Intel Compiler 等。OpenMP 提供了对并行算法的高层的抽象描述，程序员通过在源代码中加入专用的 pragma 来指明自己的意图，由此编译器可以自动将程序进行并行化，并在必要之处加入同步互斥以及通信。当选择忽略这些 pragma，或者编译器不支持 OpenMP 时，程序又可退化为通常的程序 (一般为串行)，代码仍然可以正常运作，只是不能利用多线程来加速程序执行。

OpenMP 提供的这种对于并行描述的高层抽象降低了并行编程的难度和复杂度，这样程序员可以把更多的精力投入到并行算法本身，而非其具体实现细节。对基于数据分集的多线程程序设计，OpenMP 是一个很好的选择。同时，使用 OpenMP 也提供了更强的灵活性，可以较容易的适应不同的并行系统配置。线程粒度和负载平衡等是传统多线程程序设计中的难题，但在 OpenMP 中，OpenMP 库从程序员手中接管了部分这两方面的工作。

#pragma omp parallel for num_threads()

  const uint32_t batch_size = inputs.size();
#pragma omp parallel for num_threads(batch_size)
  for (uint32_t i = 0; i < batch_size; ++i) {
    const std::shared_ptr<Tensor<float>> &input = inputs.at(i);
    CHECK(input == nullptr || !input->empty()) << "The input feature map of sigmoid layer is empty!";

    std::shared_ptr<Tensor<float>> output = outputs.at(i);
    if (output == nullptr || output->empty()) {
      output = std::make_shared<Tensor<float>>(input->shapes());
      outputs.at(i) = output;
    }

    CHECK (output->shapes() == input->shapes()) << "The output size of sigmoid is error";
    output->set_data(input->data());
    output->Transform([](const float value) {
      return 1.f / (1 + expf(-value));
    });
  }

因为for是一个语句，所以就没有#pragma大括号括起来了。根据input的size开启相同数量的线程(如果input的size过大，会不会造成线程数量过多？)，每个线程先取出特征，在做了一系列的异常处理之后，核心操作就是这句话：

    output->set_data(input->data());
    output->Transform([](const float value) {
      return 1.f / (1 + expf(-value));
    });

这里用了匿名函数，我也不知道为什么特别喜欢用匿名函数，但是我看paddle CINN里面也是大量使用，能明白其含义并且照葫芦画瓢即可。

编译 -fopenmp选项

这种创建多线程的方式简单高效，但是有一点必须注意，#pragma omp parallel关键字创建多线程必须在编译时加上-fopenmp选

项，否则起不到并行的效果，

g++ a.cc -fopenmp

算子开发模板

其实核心就两个函数，一个是重载的Forward()函数，另一个单例模式中的GetInstance()函数。

构造函数，涉及知识点：explicit用于禁止隐式转换
Forward()函数，用于核心算子功能实现。
GetInstance()函数，用于单例模式方法调用。

explicit修饰构造函数

圣经《Effective C++》在导读中这样写到：

被声明为explicit的构造函数通常比其 non-explicit 兄弟更受欢迎, 因为它们禁止编译器执行非预期 (往往也不被期望) 的类型转换. 除非我有一个好理由允许构造函数被用于隐式类型转换, 否则我会把它声明为explicit. 我鼓励你遵循相同的政策.

我觉得这篇博客里举例的隐式调用规则说的比较清楚，建议学习一下：

C++ explicit 关键字 - 知乎

所以在kuiper里面所有算子的构造函数都被explicit修饰。

  explicit SigmoidLayer(): Layer("Sigmoid"){

  }

重载函数 Forward()

C++ override从字面意思上，是覆盖的意思，实际上在C++中它是覆盖了一个方法并且对其重写，从而达到不同的作用。override是C++11中的一个继承控制关键字。override确保在派生类中声明的重载函数跟基类的虚函数有相同的声明。

override明确地表示一个函数是对基类中一个虚函数的重载。更重要的是，它会检查基类虚函数和派生类中重载函数的签名不匹配问题。如果签名不匹配，编译器会发出错误信息。

因为基类Layer的Forward是虚函数，所以子类需要用override重载

  /**
   * Layer的执行函数
   * @param inputs 层的输入
   * @param outputs 层的输出
   * @return 执行的状态
   */
  virtual InferStatus Forward(
      const std::vector<std::shared_ptr<Tensor<float>>>& inputs,
      std::vector<std::shared_ptr<Tensor<float>>>& outputs);

  /**
   * Layer的执行函数
   * @param current_operator 当前的operator
   * @return 执行的状态
   */
  virtual InferStatus Forward();

  InferStatus Forward(const std::vector<std::shared_ptr<Tensor<float>>> &inputs,
                      std::vector<std::shared_ptr<Tensor<float>>> &outputs) override;

单例模式 GetInstance()

这个上一讲详细讲过，不多赘述。

KuiperInfer深度学习推理框架-源码阅读和二次开发(1)：算子开发流程之算子注册机制详解_沉迷单车的追风少年的博客-CSDN博客

测试文件

单测能力是依赖Google Test的，代码中的TEST是一个宏，用来创建测试用例，它有test_case_name和test_name两个参数，分别是测试用例名和测试名。

一些基础的测试知识请看：

一文掌握google开源单元测试框架Google Test - 知乎

我们如何测试算子是否正确呢？我们需要“手动”实现一遍逻辑，然后看这两者之间的结果是否相等。

这里手动实现的核心是我们要调用 1.f / (1 + std::exp(-input_->index(j)) 来验证是否正确，注意单元测试要尽可能覆盖所有特殊的样例！

TEST(test_layer, forward_sigmoid4) {
  using namespace kuiper_infer;
  std::shared_ptr<Tensor<float>> input = std::make_shared<Tensor<float>>(1, 32, 128);
  input->Rand();
  std::vector<std::shared_ptr<Tensor<float>>> inputs;
  inputs.push_back(input);
  std::vector<std::shared_ptr<Tensor<float>>> outputs(1);

  SigmoidLayer sigmoid_layer;
  const auto status = sigmoid_layer.Forward(inputs, outputs);
  ASSERT_EQ(status, InferStatus::kInferSuccess);
  for (int i = 0; i < inputs.size(); ++i) {
    std::shared_ptr<Tensor<float>> input_ = inputs.at(i);
    std::shared_ptr<Tensor<float>> output_ = outputs.at(i);
    CHECK(input_->size() == output_->size());
    uint32_t size = input_->size();
    for (uint32_t j = 0; j < size; ++j) {
      ASSERT_EQ(output_->index(j), 1.f / (1 + std::exp(-input_->index(j))));
    }
  }
}

单测当中就没有必要写#program并行了，直接逐个遍历即可。

NCNN实现借鉴

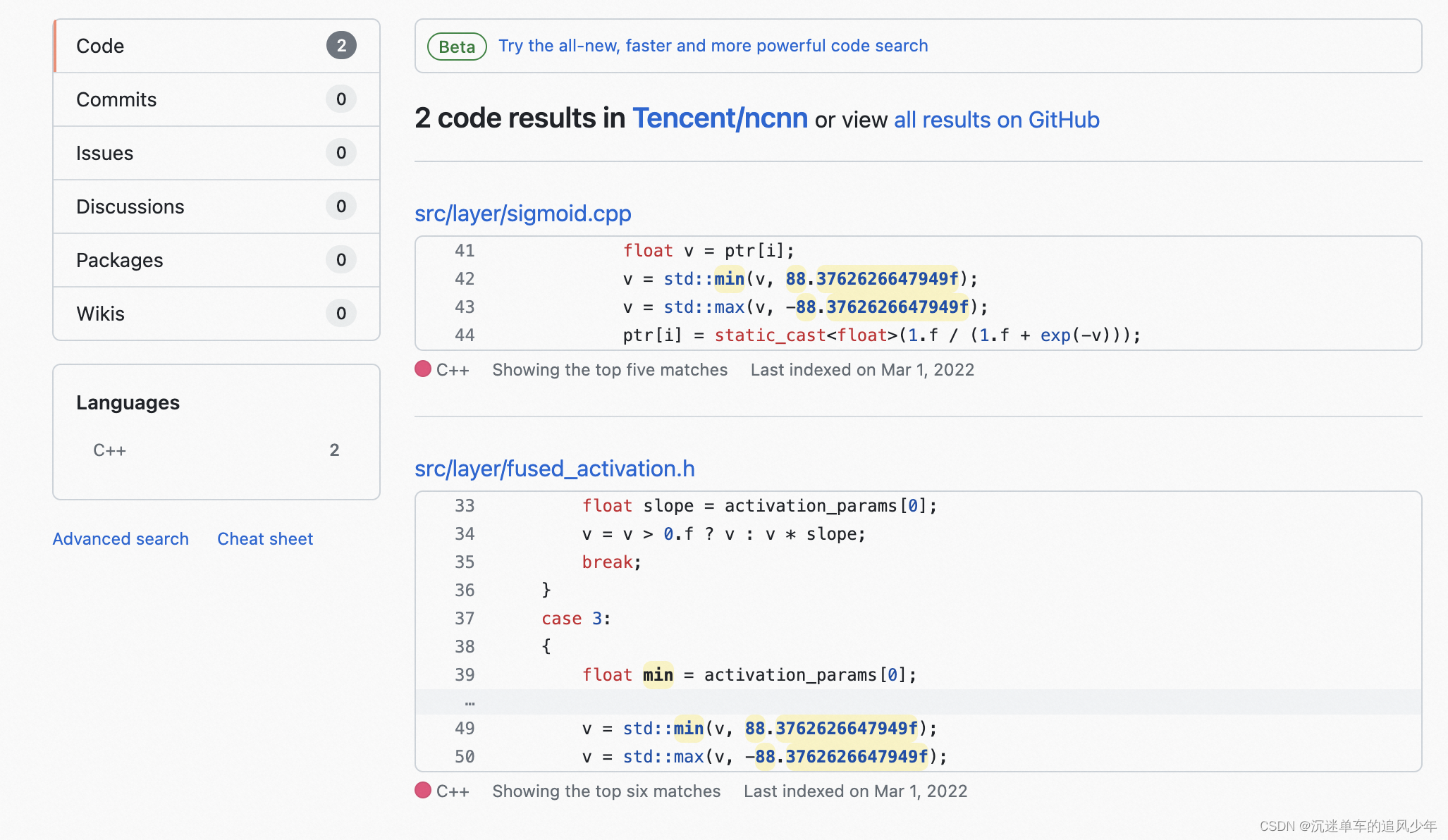
NCNN当然要认真抄袭借鉴了！实现在这个文件中：https://github.com/Tencent/ncnn/blob/7886e90c65ec995159427e9e98bf9520683f661e/src/layer/sigmoid.cpp

int Sigmoid::forward_inplace(Mat& bottom_top_blob, const Option& opt) const
{
    int w = bottom_top_blob.w;
    int h = bottom_top_blob.h;
    int channels = bottom_top_blob.c;
    int size = w * h;

    #pragma omp parallel for num_threads(opt.num_threads)
    for (int q = 0; q < channels; q++)
    {
        float* ptr = bottom_top_blob.channel(q);

        for (int i = 0; i < size; i++)
        {
            float v = ptr[i];
            v = std::min(v, 88.3762626647949f);
            v = std::max(v, -88.3762626647949f);
            ptr[i] = static_cast<float>(1.f / (1.f + exp(-v)));
        }
    }

    return 0;
}

功能上是用<math.h>中的exp()实现的，为了处理溢出，ncnn专门用了这种方式去处理，我还没有见过……

            v = std::min(v, 88.3762626647949f);
            v = std::max(v, -88.3762626647949f);

不过我看一些其他地方也用了，值得学习哈！

后记

这篇博客完全是自己的个人笔记，仅供自我参考！还是强烈建议去看up主的教程！

参考

https://www.jianshu.com/p/4528da002c43
C/C++中关于 #pragma 的深度探究_c++ #pragma_华枝歌的博客-CSDN博客
KuiperInfer深度学习推理框架-源码阅读和二次开发(1)：算子开发流程之算子注册机制详解_沉迷单车的追风少年的博客-CSDN博客
C++-[override]关键字使用详解_c++ override_Planet^沐的博客-CSDN博客