高级精度算法系列

第一章 简单实现
第二章 压位优化
第三章 二进制优化(本章)

---

---

前言

上一章《C/C++ 高精度（加减乘除）算法压位优化》实现了优化的高精度计算，采用int32的整型数组每个元素可以储存9个10进制数字，想要再进一步优化计算速度，可以改变数据存储方式，采用二进制存储数字。依然采用int32数组其元素通过二进制来存储数字，这样做不仅运算效率高，而且空间利用率也达到了最高。

---

一、基本原理

1、存储方式

存储二进制顺序由低到高位存储

2、计算方式

计算方式与10进制存储计算方式基本一致，下面给出int8的计算方式，int16、int32以此类推本质是一样的。

---

二、关键实现

1、整型转高精度数组（二进制）

通过位操作既可以实现(元素类型int32为例)：

/// <summary>
/// 通过无符号整型初始化
/// </summary>
/// <param name="a">[in]高精度数组</param>
/// <param name="value">[in]整型值</param>
static void loadInt(int* a, uint64_t value) {
	a[1] = (uint32_t)value;
	a[2] = value >> (sizeof(int) * 8);
	a[0] = a[2] ? 2 : 1;
}

2、字符串转高精度数组（二进制）

在这里提供一种方法，此方法需要先实现高精度加以及乘。
（1）初始化高精度数组值为0
（2）逐个获取字符串中的数字
（3）高精度数组乘等于10
（4）获取的数字与高精度数组相加（整型转高精度数组参考上一节）
（5）字符串未读取完回到（2）

3、高精度数组（二进制）转字符串

这里提供一种方法，需要上一章的实现作为辅助《C/C++ 高精度（加减乘除）算法压位优化》
（1）初始化压9位高进度数组值为0
（2）逐个获取高精度数组（二进制）的元素
（3）压9位高进度数组乘等于2^32（二进制数组元素类型int32为例）
（4）获取的元素与9位高进度数组相加
（5）元素未读取完回到（2）
（6）压9位高进度数组转字符串

---

三、完整代码

因为接口以及使用方法与第一章《C/C++ 高精度（加减乘除）算法简单实现》是完全一致的，所以这里只提供完整代码，使用示例请参考第一章。
基于int32数组二进制存储实现的高精度算法：
https://download.csdn.net/download/u013113678/87720242

---

四、性能对比

测试平台：Windows 11
测试设备：i7 8750h
测试方式：测试5次取均值
表1、测试用例

测试用例	描述
1	整型范围数字计算500000次
2	长数字与整型范围数字计算500000次
3	长数字与长数字计算500000次

基于上述用例编写程序进行测试，测试结果如下表
表2、测试结果

计算	测试用例	压9位优化（上一章）耗时	二进制优化int32（本章）耗时
加法	测试用例1	0.002620s	0.0024862s
加法	测试用例2	0.005711s	0.0034712s
加法	测试用例3	0.005384s	0.003857s
累加	测试用例1	0.002536s	0.0027246s
累加	测试用例2	0.002592s	0.0029876s
累加	测试用例3	0.006474s	0.0043758s
减法	测试用例1	0.002078s	0.0022704s
减法	测试用例2	0.004939s	0.0032914s
减法	测试用例3	0.004929s	0.0041246s
累减	测试用例1	0.002034s	0.0020808s
累减	测试用例2	0.001942s	0.0023542s
累减	测试用例3	0.004282s	0.0044144s
乘法	测试用例1	0.004751s	0.0038996s
乘法	测试用例2	0.028358s	0.0117986s
乘法	测试用例3	0.064259s	0.0185958s
累乘	测试用例1 只计算1000次	0.000137s	0.000062s
累乘	测试用例2 只计算1000次	0.000187s	0.0000816s
累乘	测试用例3 只计算1000次	0.081988s	0.0292832s
除法	测试用例1	0.024763s	0.0196498s
除法	测试用例2	0.516090s	0.3556564s
除法	测试用例3	0.073812s	0.1716874s
累除	测试用例1 只计算1000次	0.035722s	0.0009416s
累除	测试用例2 只计算1000次	0.060936s	0.0131722s
累除	测试用例3 只计算500次	25.126072s	2.6210544s

将上表数据进行分类相同类型取均值计算出提升速度如下图所示，仅作参考。

图1、速度提升

---

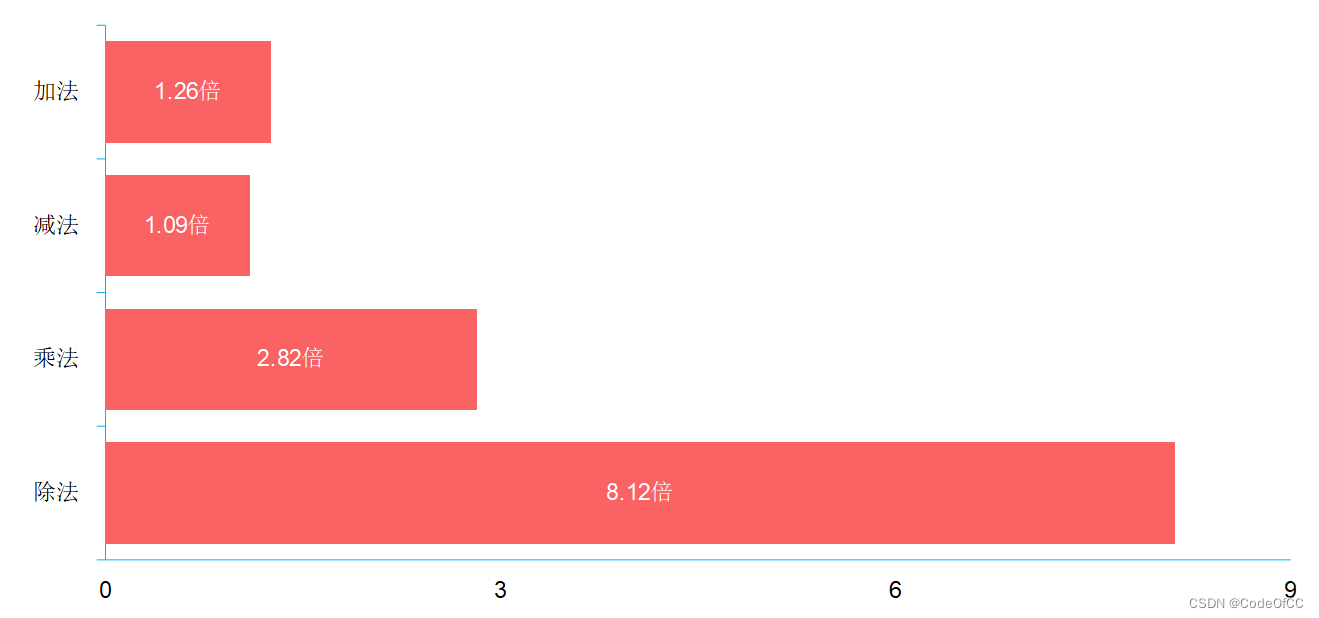
总结

以上就是今天要讲的内容，二进制存储优化在对比压9位优化速度还有提升，而且存储方式与整型一样，很好的利用了空间。相比较与压9位算法，二进制算法对于乘法和除法的提升较大，尤其是长数据运算的提升更为明显。本章算法的二进制转换方法实现参考了c# 的BigInt，总的来说，这是一个性能比较好的高精度算法，比较适用于项目开发。

---