前言

本文将基于UoA的课件，连接上一篇博文介绍机器学习中的贝叶斯。看不太懂的读者请先阅读：贝叶斯学习（Bayesian Learning）基础篇

涉及的英语比较基础，所以为节省时间（不是full-time，还有其他三门课程，所以时间还是比较紧的），只在我以为需要解释的地方进行解释。

此文不用于任何商业用途，仅仅是个人学习过程笔记以及心得体会，侵必删。

Review Bayes Optimal Classifier

Bayes Optimal Classifier, also known as Bayes classifier, is a probabilistic model used for classification tasks. It is based on Bayes’ theorem and makes a decision based on the posterior probability of each class given the observed data.

The Bayes Optimal Classifier assumes that the distribution of the input data and the conditional probabilities of each class given the data are known. It then computes the posterior probability of each class given the data and chooses the class with the highest posterior probability as the classification result.

One of the advantages of the Bayes Optimal Classifier is that it is theoretically optimal, meaning it achieves the lowest possible classification error rate for any given distribution of the data. However, in practice, it may be difficult to estimate the distribution of the data accurately, and the assumptions made by the model may not hold.

The Bayes Optimal Classifier is often used as a benchmark for evaluating the performance of other classifiers, and it serves as a theoretical foundation for many probabilistic classification methods such as Naive Bayes, Bayesian Networks, and Bayesian Linear Regression.

Naive Bayes Classifier

For the concept

The Naive Bayes Classifier is a probabilistic algorithm that is commonly used for classification tasks. It is based on the Bayes theorem and applies to learning tasks where each instance is described by a conjunction of attribute values and where the target function can take on any value from some finite set.

In other words, the Naive Bayes Classifier is used when we have a set of attributes that describe an instance, and we want to predict the value of a target variable based on these attributes. The attributes are assumed to be independent of each other, and this assumption is known as the “naive” assumption, hence the name “Naive Bayes”.

For example, consider a dataset of emails that are labeled as either spam or not spam. Each email is described by a set of attributes such as the presence of certain words or phrases, the length of the email, etc. The target variable is the label (spam or not spam) that we want to predict for new emails. The Naive Bayes Classifier can be used to learn a model from this data, which can then be used to predict the label of new emails based on their attributes.

First, given the training data D, we can estimate the probability of each target value Vj by counting its frequency in D.

However, estimating the joint probability of all attribute values and target value P(a1, a2, …, an | Vj) is not feasible because the number of possible instances is too large (|all possible instances| x |V|).

To simplify the problem, the naive Bayes classifier assumes that the attribute values are conditionally independent given the target value. This means that knowing the value of one attribute does not affect the probability distribution of other attributes given the target value.

The text then gives an example of conditional independence, where X and Y are conditionally independent given Z if P(X,Y|Z) = P(X|Z)P(Y|Z).

With this assumption of conditional independence, we can estimate P(a1 | Vj), P(a2 | Vj), …, P(an | Vj) separately and multiply them together to get the joint probability P(a1, a2, …, an | Vj). This simplifies the calculation and makes it feasible to estimate the joint probabilities from the training data.

这里其实不太懂

Example

例子还是很好看懂的，其实就是画一个图表然后算出对应的值，以及一些常见数据缺失时或者异常的处理方式。

我们希望通过对三个分类特征的测量来学习将标记为“+”的对象与标记为“-”的对象区分开来。这里的“分类特征”指的是离散型的特征，例如颜色、形状等，而“测量”则是指对这些特征进行量化或者编码的操作，使它们可以作为模型输入。

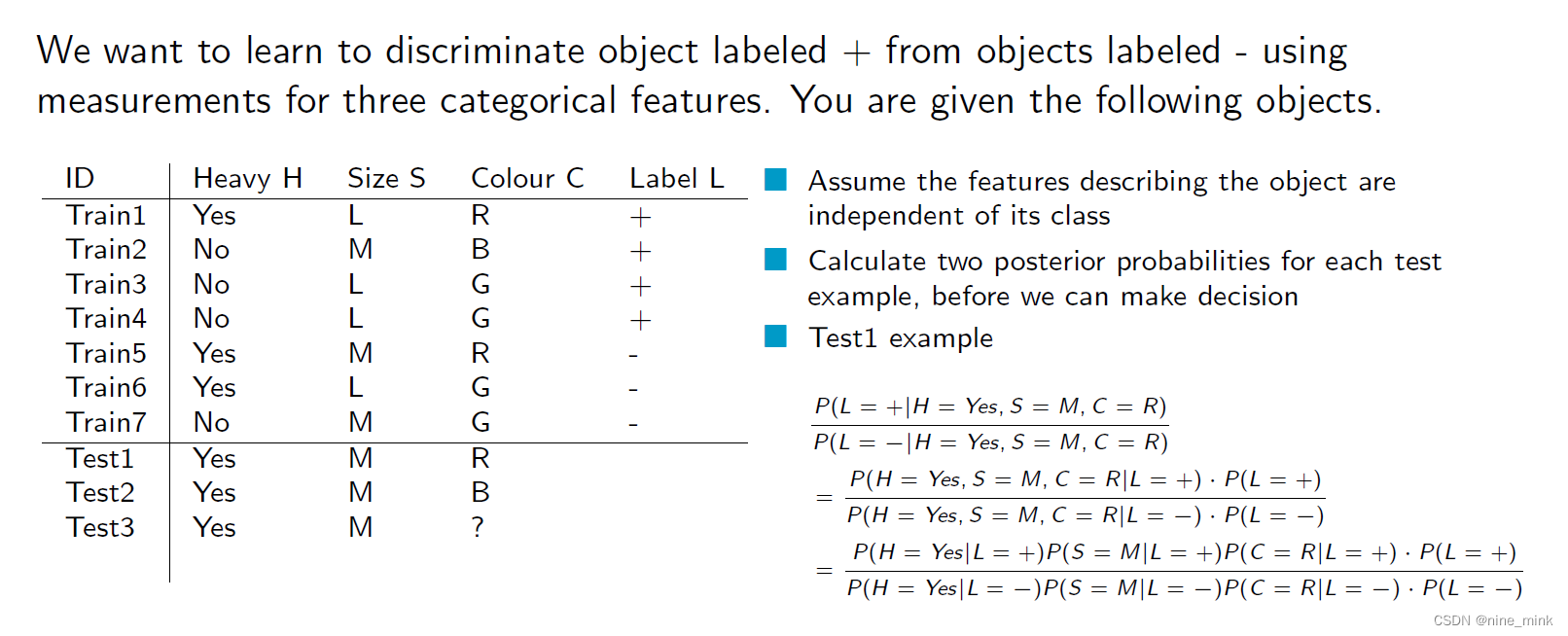
当我们的训练集很小但属性值很多时，观察到的分数会是不准确的。当属性值为零时，这将会在所有具有该属性值的测试样本计算中占据主导地位。因为在朴素贝叶斯中，如果一个特征在训练集中没有出现过，则它的条件概率为零，这会导致概率计算的不准确性。因此，需要采取一些方法来解决这个问题，例如添加平滑项来避免概率为零。

Laplace smoothing

Laplace smoothing是一种常用的概率平滑技术，用于处理在离散数据上的概率估计。在概率估计中，经常会遇到某些离散属性的概率值为零的情况，这种情况下可能会影响到模型的性能。为了解决这个问题，可以使用Laplace smoothing技术，它在计算概率时，为每个属性值都添加一个平滑因子，这个平滑因子通常是一个小的正数，这样就避免了概率值为零的情况，同时保持了概率值的相对大小关系。Laplace smoothing可以有效地解决数据稀疏性问题，提高了模型的鲁棒性。

加完之后原数据的比例会发生变化

加完 Laplace smoothing 后，原始数据中每个属性值对应的比例会发生微小的变化。这是因为 Laplace smoothing 会为每个属性值加上一个小的常数，相当于给每个属性值都增加了一个虚拟的观测次数，这样就会略微改变原始数据中每个属性值的比例。但是，这种变化很小，不会对贝叶斯分类器的性能产生明显影响。

分子+1，如何确定分母的加数

在 Laplace smoothing 中，分母的加数是类别的数量，通常是训练数据中类别的总数。在进行加法平滑之前，我们需要计算每个类别中每个属性值的出现次数，以便确定需要加多少次平滑项。

例如，对于一个二分类问题，我们有两个类别：正类和负类。假设在训练数据中，属性 a 的取值为 x 时，正类出现了 2 次，负类出现了 1 次，属性 a 的取值为 y 时，正类出现了 1 次，负类出现了 2 次。如果我们使用 Laplace smoothing，那么我们需要将每个属性值的出现次数加上 1，然后再将分母加上属性值的总数，即：

• 对于属性 a 的取值为 x，正类的计数变为 2+1=3，负类的计数变为 1+1=2。
• 对于属性 a 的取值为 y，正类的计数变为 1+1=2，负类的计数变为 2+1=3。
• 分母加上属性值的总数，即 2（属性 a 有两个取值：x 和 y）。

这样，我们就可以使用平滑后的计数来估计每个属性值在每个类别中的概率，以便进行分类

Naive Bayes for Document Classi cation

Problem statement

假设我们有一个已经标记好类别的文档数据集，并且有一个未标记类别的文本文档 d，还有一组可能的文档类别 C，我们希望找到最有可能的文档类别 c，使得该文本文档 d 属于类别 c。也就是说，我们希望用已有的数据集中的信息，对未知的文档进行分类。

Document representation

Naive Bayes for Document Classi cation

朴素贝叶斯分类器中的参数估计是基于条件独立性假设的，即假设在给定类别的情况下，各个特征之间是相互独立的。因此，对于具有 n 个特征的数据集，我们只需要估计 n 个条件概率（或条件概率的参数），因为这些参数可以独立地估计。

具体而言，对于每个特征，我们需要估计在每个类别下的条件概率，共计 n * |C|个参数，其中 n 是特征的数量，|C| 是类别的数量。另外，还需要估计 |C| - 1 个类别的先验概率(对于c个类别，只需要估计c-1个类别的先验概率，是因为它们的和为1，因此可以通过1减去其他类别的先验概率得到)，因此一共需要估计 n * |C| + |C| - 1 个参数。

这些参数估计的过程通常通过使用训练数据集进行统计计算得到，例如使用极大似然估计、贝叶斯估计等方法。这些参数估计后，就可以在朴素贝叶斯分类器中使用它们进行分类预测

假设： 在给定文档类别的情况下，每个单词出现的概率是相同的，并且这个概率不依赖于单词在文档中出现的具体位置。换句话说，它表达了朴素贝叶斯分类器中的“朴素”假设，即每个单词的出现是相互独立的，且对于分类结果的影响是一样的。

上面公式的含义： 对于给定的一个类别c和一个单词w，在所有标记为c的文档中，单词w出现的次数除以所有单词出现的次数之和，就是单词w在类别c中的条件概率P(xi=w|c)。其中，count(w, c)表示单词w在所有标记为c的文档中出现的次数，count(x, c)表示类别c中单词出现的总次数，Σ表示对所有单词x求和。换句话说，这个式子是朴素贝叶斯算法中用来计算每个单词在每个类别中的条件概率。

An Illustrative Example

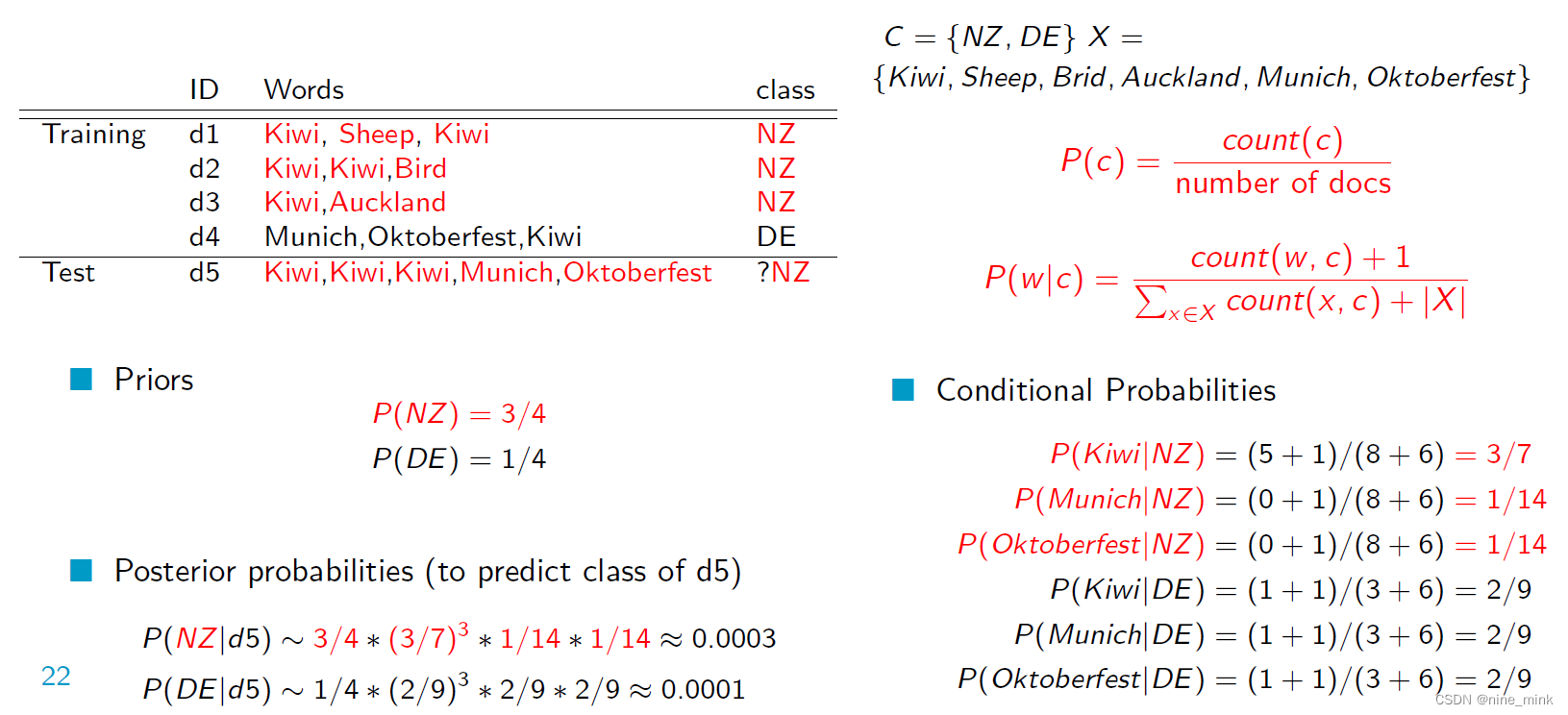
这是一个朴素贝叶斯分类器的例子，用于将测试文档d5分类为NZ或DE。

首先，我们需要计算类别的先验概率。在这个例子中，NZ出现在3个文档中，DE出现在1个文档中，因此P(NZ) = 3/4，P(DE) = 1/4。

然后，我们需要计算每个类别中每个单词的条件概率。例如，P(Kiwi|NZ)表示在给定文档为NZ的情况下，单词“Kiwi”出现的概率。为了计算这个概率，我们需要计算“Kiwi”在所有NZ文档中出现的次数，即count(Kiwi, NZ) = 3，以及在所有NZ文档中出现的单词总数，即count(x, NZ) = 8+6 = 14。因此，P(Kiwi|NZ) = (3+1)/(8+6) = 3/7。同样的，我们可以计算其他单词在每个类别中的条件概率。

最后，我们可以计算后验概率来预测测试文档d5的类别。我们需要将测试文档中的单词的条件概率乘起来，并乘以类别的先验概率。例如，P(NZ|d5) = P(Kiwi|NZ)³ * P(Munich|NZ) * P(Oktoberfest|NZ) * P(NZ) = (3/7)³ * (1/14) * (1/14) * (3/4) = 0.0003。同样的，我们可以计算P(DE|d5)。根据贝叶斯准则，后验概率最大的类别将被预测为测试文档的类别。在这个例子中，测试文档d5将被预测为NZ类别，因为P(NZ|d5) > P(DE|d5)。

Discussion

朴素贝叶斯分类器对以下情况是否受到影响/具有鲁棒性：

1. 孤立的噪声样本？
   孤立的噪声样本会对朴素贝叶斯分类器产生一定影响，因为它们可能会导致模型的偏移。但是，如果噪声样本的数量相对于训练集的大小非常小，那么对模型的影响就会被减小。

2. 无关属性？
   无关属性对朴素贝叶斯分类器具有一定的鲁棒性，因为它们不会对其他属性的权重产生太大的影响，从而不会对分类结果造成太大的干扰。但是，如果无关属性的数量过多，可能会对模型的精度产生一定的影响。

3. 缺失值？
   缺失值会对朴素贝叶斯分类器产生影响，因为缺失值可能导致模型无法正确地学习有关特征的信息。一些处理方法，如插值法，可以帮助缓解缺失值对模型的影响。

4. 相关属性？
   相关属性会对朴素贝叶斯分类器产生影响，因为它们可能导致模型的偏差，即当一个属性出现时，另一个属性也可能出现。但是，如果相关性不是非常强，朴素贝叶斯分类器仍然可以产生良好的分类结果。

Summary

朴素贝叶斯分类器通过使用训练数据来学习估计P(X|Y)和P(Y)的概率分布来学习一些目标函数f:X->Y，或等价地，学习P(Y|X)。然后可以使用这些估计的概率分布和贝叶斯定理对新的X样本进行分类。

问题是通常需要训练样本数量超出输入（属性）空间上可能实例的数量，这是不现实的。

解决方法是朴素贝叶斯分类器假设在给定Y的情况下，描述X的所有属性是条件独立的，从而大大减少了必须估计学习分类器的参数数量（这意味着更小的训练数据集就足以完成学习任务）。

Bayesian Networks

在朴素贝叶斯中，对条件独立性的假设过于严格，但是如果不做这个假设，计算会变得非常复杂。贝叶斯信念网络允许在变量子集之间存在条件独立性，这样就可以将先前关于变量之间独立性的知识与观测到的训练数据相结合，更好地进行推断和预测。简单来说，它是一种可以灵活处理变量之间关系的方法。

Bayesian Belief Networks

贝叶斯网络是一种简单的图形符号，用于表示条件独立关系和完整联合分布的紧凑规范。它包含了一组节点，每个节点对应一个随机变量Xi，以及一组有向边，每个边表示随机变量之间的影响方向。它是一个有向无环图，每个节点都有一个条件概率分布，给出它的父节点的条件下Xi的概率分布。这个条件分布用一个条件概率表来表示，它给出了每个父节点取值组合下Xi的分布。这种网络可以用来表示先验知识和从数据中学习的知识，以进行推断和预测。

Joint Distribution

联合分布指的是多个随机变量的取值组成的所有可能性的概率分布。假设有两个随机变量X和Y，它们的联合分布就是指对于X和Y的每一个可能取值的组合，它们同时发生的概率，可以用一个二维表格来表示。例如，假设X可以取值为1、2、3，Y可以取值为"a"、“b”，那么联合分布就是一个3x2的表格，其中每个单元格里的值就是对应取值组合的概率。

Bayesian Belief Networks - Variable Relationships

Bayesian Belief Networks是一种图形模型，用于描述变量之间的依赖关系。通过将节点标记为Xi，使得只有i<j时Xi才是Xj的祖先，可以使用概率的链式规则和局部马尔可夫性将联合概率分解为一系列条件概率的乘积，其中每个节点的概率由其父节点决定。例如，P(X1, X2, X3, X4,X5) = P(X1)P(X2)P(X3jX1,X2)P(X4jX2)P(X5jX4)。这样的图形模型可以很好地表示变量之间的依赖关系，并指定它们的联合概率分布。

关于P(X1, X2, X3, X4,X5) = P(X1)P(X2)P(X3jX1,X2)P(X4jX2)P(X5jX4)

Bayesian Belief Networks是基于联合概率分布的因式分解的，因此可以使用链式法则对其进行拆解。具体地，我们可以将联合概率分布拆分成多个条件概率分布的积，如下所示：

P(X1, X2, X3, X4, X5) = P(X1) * P(X2|X1) * P(X3|X1,X2) * P(X4|X1,X2,X3) * P(X5|X1,X2,X3,X4)

但是，由于Bayesian Belief Networks中每个节点只依赖于其父节点，因此可以使用局部马尔可夫性质简化此拆解。换句话说，每个节点只与其父节点有关，与其他节点无关，因此可以用该节点的父节点的条件概率分布来表示该节点的条件概率分布。这使得我们可以将联合概率分布进一步分解为以下形式：

P(X1, X2, X3, X4,X5) = P(X1)P(X2|X1)P(X3|X1,X2)P(X4|X2)P(X5|X4)

这是一个更简洁的形式，其中每个条件概率分布只依赖于它的父节点。

Local Markov

在贝叶斯网络中，每个节点表示一个随机变量。Local Markov性质指的是，一个节点在给定它的父节点的情况下，与它的非后代节点是条件独立的。换句话说，一个节点与它的所有祖先节点和子孙节点的联合分布只依赖于它的父节点。这个性质对于简化网络的结构和计算概率分布非常重要。

Bayesian Belief Network - Example

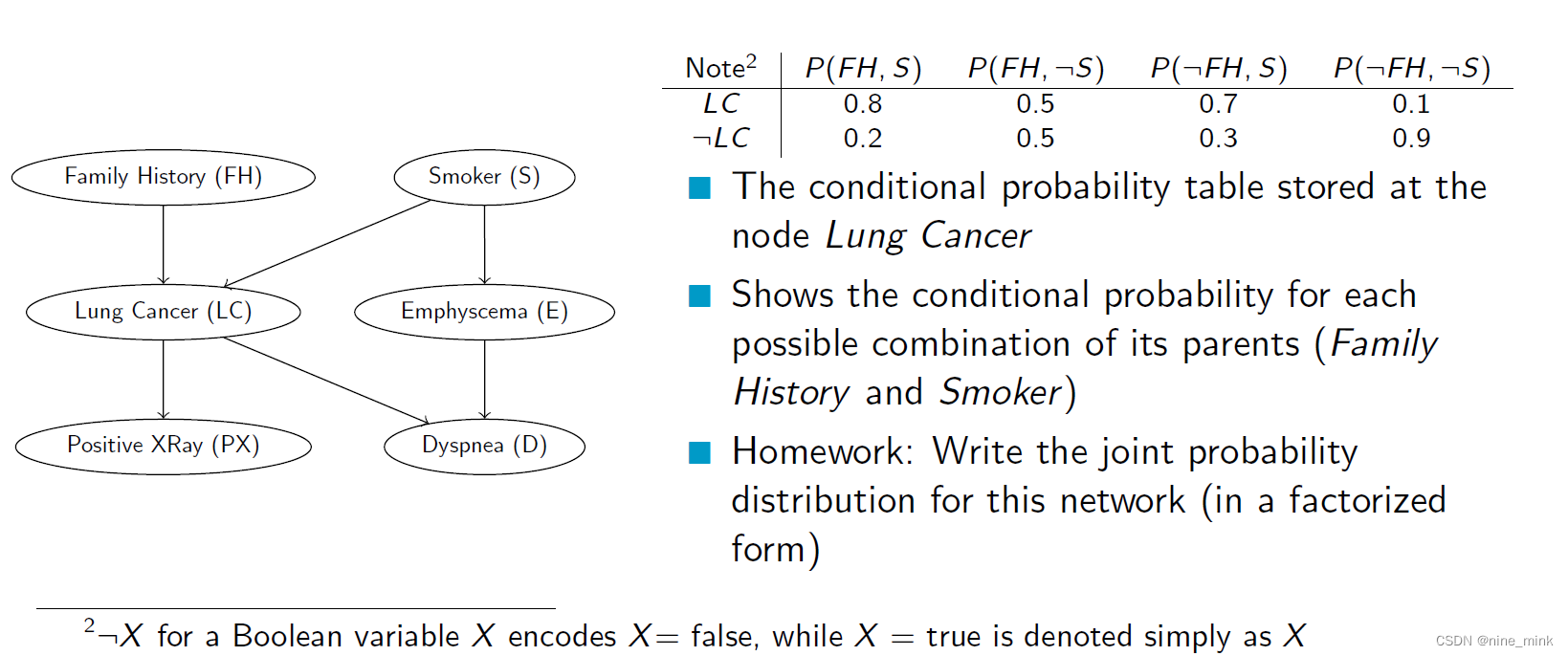
Bayesian (Belief) Network - Another Example

Application: Naive Bayes Classi er

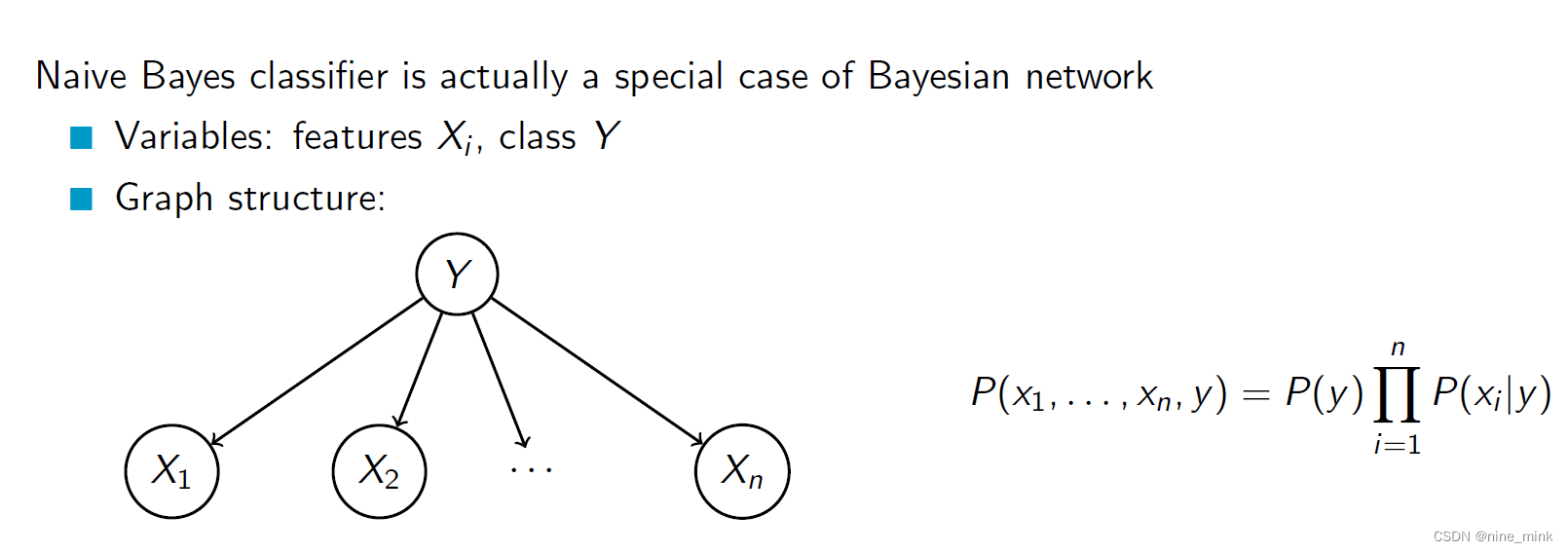朴素贝叶斯分类器可以看作是贝叶斯网络的一个特例。在朴素贝叶斯分类器中，我们假设所有属性在给定类标签的条件下都是条件独立的，这意味着每个属性节点只有一个父节点，即类标签节点。因此，朴素贝叶斯分类器可以看作是一个贝叶斯网络，其中只有一个父节点和多个子节点。这种假设虽然过于简化，但在许多实际情况下是有效的，因为它能够处理高维度的数据并且不需要大量的训练数据。

Application: Hidden Markov Model

隐马尔可夫模型 (Hidden Markov Model, HMM) 是一种基于概率的生成模型，它被广泛应用于时间序列数据的建模和分析中。HMM 由一组状态、一组可能的观测值以及两组概率构成，分别是状态转移概率和发射概率。状态转移概率描述了在不同时间步转移到不同状态的概率，发射概率描述了在每个状态下生成观测值的概率。HMM 假设状态是隐藏的（无法直接观测），而只能观测到对应状态下的观测值。

HMM 可以用贝叶斯网格表示，其中隐含状态形成了一个马尔可夫链，而观测变量则从各个状态中独立地生成。HMM 的前向算法和后向算法可以通过贝叶斯网格的局部概率计算得出。通过 HMM 建模，可以解决很多实际问题，比如语音识别、自然语言处理、手写字识别等。

Inference in Bayesian Networks

贝叶斯网络可以用来推断一个或多个变量的概率分布，假设已知其他变量的观测值。推断的过程是基于贝叶斯定理，根据先验概率和观测数据得到后验概率。具体而言，假设我们要推断变量X的概率分布，已知观测变量Y的取值为y，贝叶斯定理表示为：

P(X|Y=y) = P(Y=y|X)P(X) / P(Y=y)

其中，P(Y=y|X)表示给定X时Y=y的条件概率，P(X)表示X的先验概率，P(Y=y)是归一化因子，保证后验概率分布的总和为1。在推断过程中，需要计算所有可能取值的X的后验概率分布，即P(X|Y=y)，然后根据需要进行预测或决策。

推断祖先的方法与推断后代的方法类似，可以使用贝叶斯网络中的概率推断方法。给定已知祖先节点的值，可以使用联合概率分布和条件概率分布计算推断目标节点的概率分布。如果祖先节点也是未知的，则可以使用相同的推断方法进行递归推断，直到所有未知节点的概率分布都被推断出来为止。然而，这种递归推断方法可能会导致计算复杂度非常高，尤其是当网络结构复杂时。

Summary

• 贝叶斯最优分类器结合了由后验概率加权的所有备选假设的预测

• 贝叶斯网络为条件独立性提供了一种自然的表示

• 朴素贝叶斯分类器一种简单快速的分类方法，它假设给定目标值的属性值是有条件独立的。