一般都是单向量输入,但是如果多向量输入应该如何处理呢?引出自注意力机制
多向量输入可能会有多种输出,如果输入n个向量,输出n个向量表明这是sequence labeling,比如对于一个英文句子,每一个单词都判断是什么词性
输入n个向量,输出1个向量,这是常见的classification问题,也就是分类问题,比如通过语音识别出是哪个人
输入n个向量,不知道会输出多少个向量,这是seq2seq问题,sequence to sequence,比如语音识别,对声音片段分解然后识别什么意思,还有翻译,输入n个中文,不一定会输出n个英文单词
用第一个n输入n输出举例,比如现在有一个英文句子 I saw a saw,我看见了一个锯子,应该分别输出名词、动词、冠词和名词,但是对于同一个单词saw一个输出了动词,第二个却输出名词,这会让人工智能非常疑惑,为什么同一个输入会输出不同的结果,其实是因为没有结合上下文,由此我们可以提出联系上下文,也就是用一个window,假设我们设window的大小为3,判断每一个单词,我们都需要判断它的上一个自身和下一个,这样可以起到一定的作用,但是window具体要开多大又引出了一个问题
我们输入的句子不可能永远都是只有4个单词,输入的句子长短不一,对于短句子,这个window的大小可能合适,但是对于比较长的句子,那么这么窄的window显然效果不会很好,如果我们先从输入中找到长度最长的句子,然后根据它设定window的长度,但是这样也会出现一个问题,那就是window如果设置太大会出现效率比较低的情况,有没有更好的方法能解决这种问题呢?引出正题自注意力机制
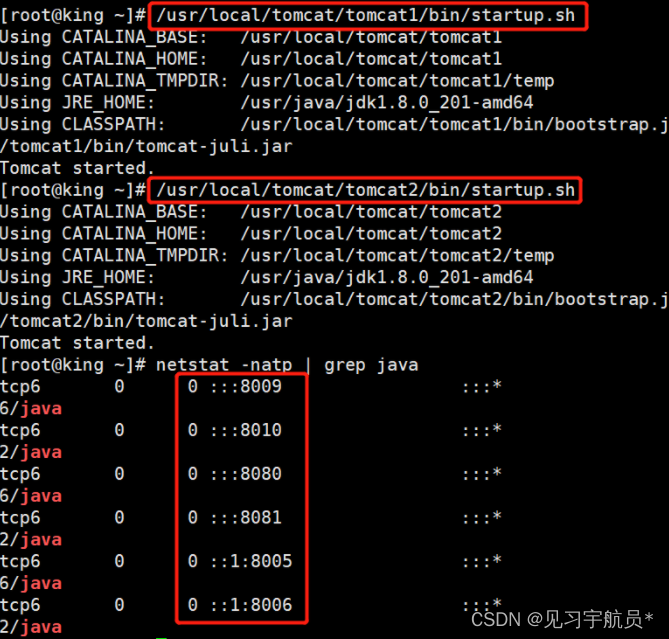
还是上述的句子,我们可以让输入的向量经过一个self-attention层输出,这个self-attention对于每一个输入的向量首先得出自身与其他向量的关联性α,又称attention score,具体是怎么得到的呢,我们采用一种dot-product的方式,首先让当前的向量乘一个矩阵,将另外一个矩阵也乘一个矩阵,这两个得出的结果再点积获得α,这种方法也被用于transformer这种模型,下图中的W即为矩阵
通常自身和自身也要计算出关联性
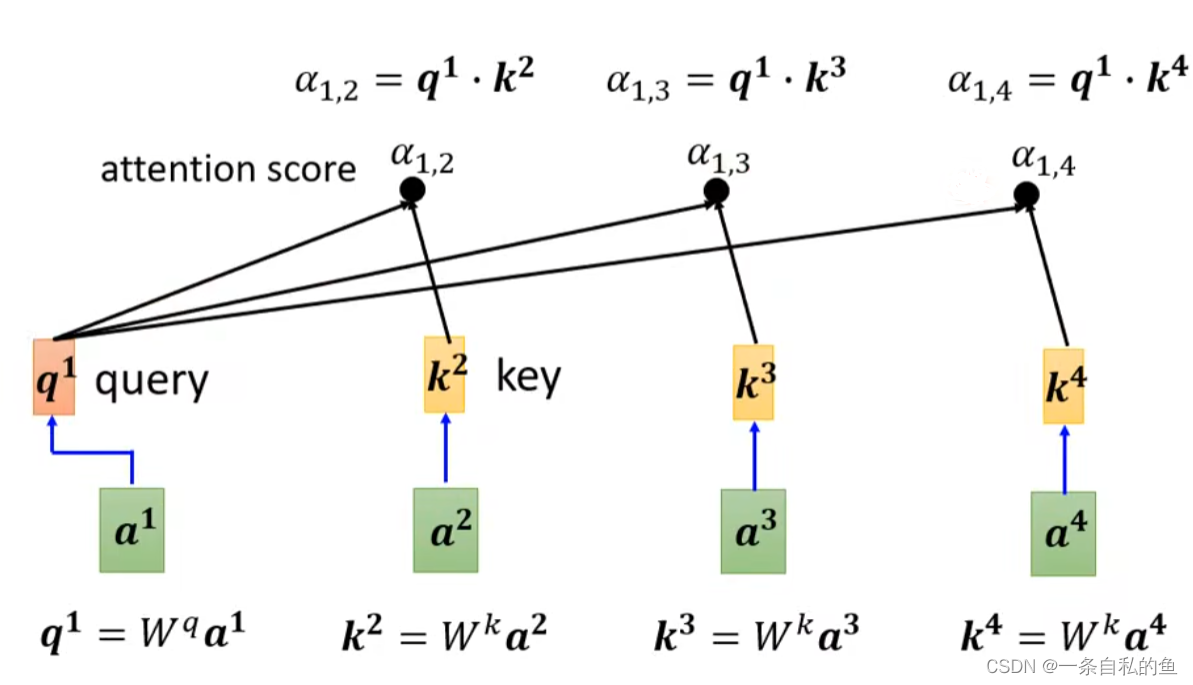
然后再用一个矩阵乘上每一个向量得出v,最后将v和关联性α相乘再相加得出当前这个向量的输出值,这样处理的话,跟当前向量关系比较大的关联性α权重也大,也就贡献比较多
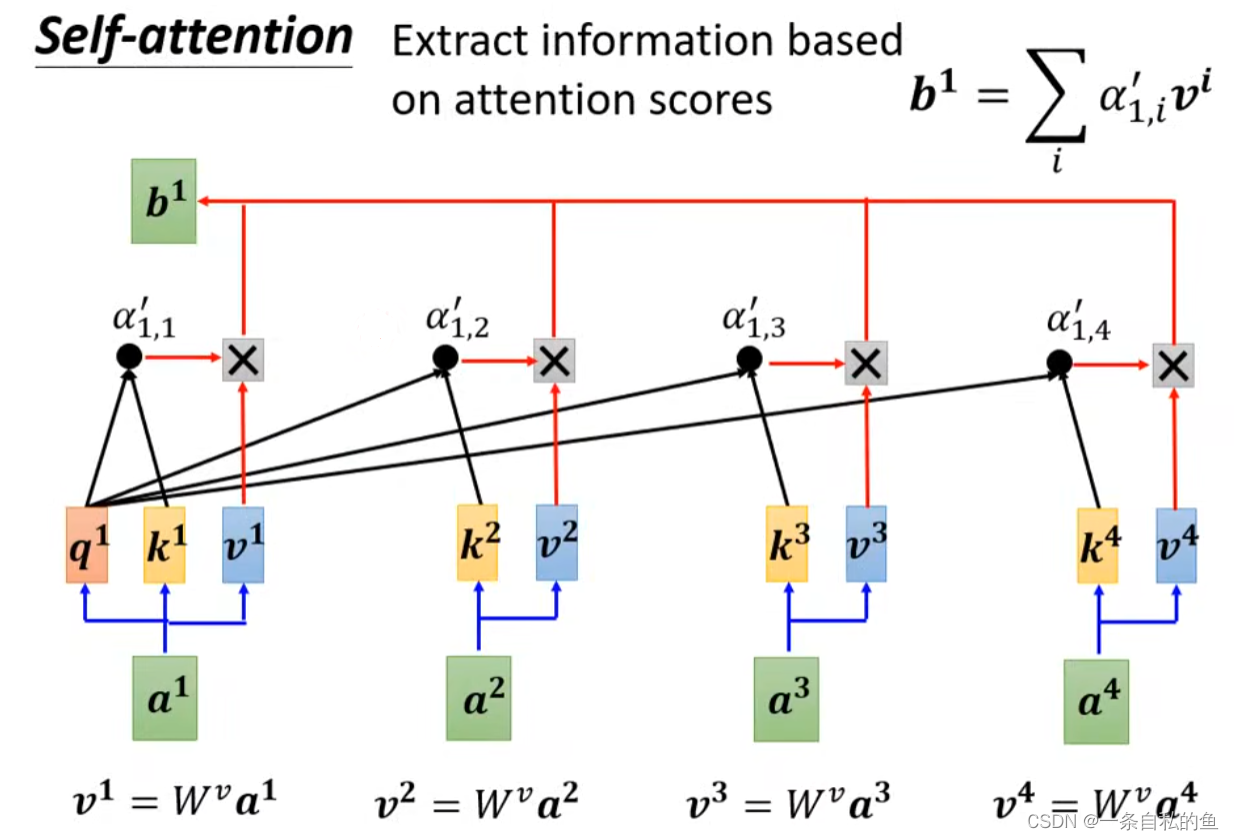
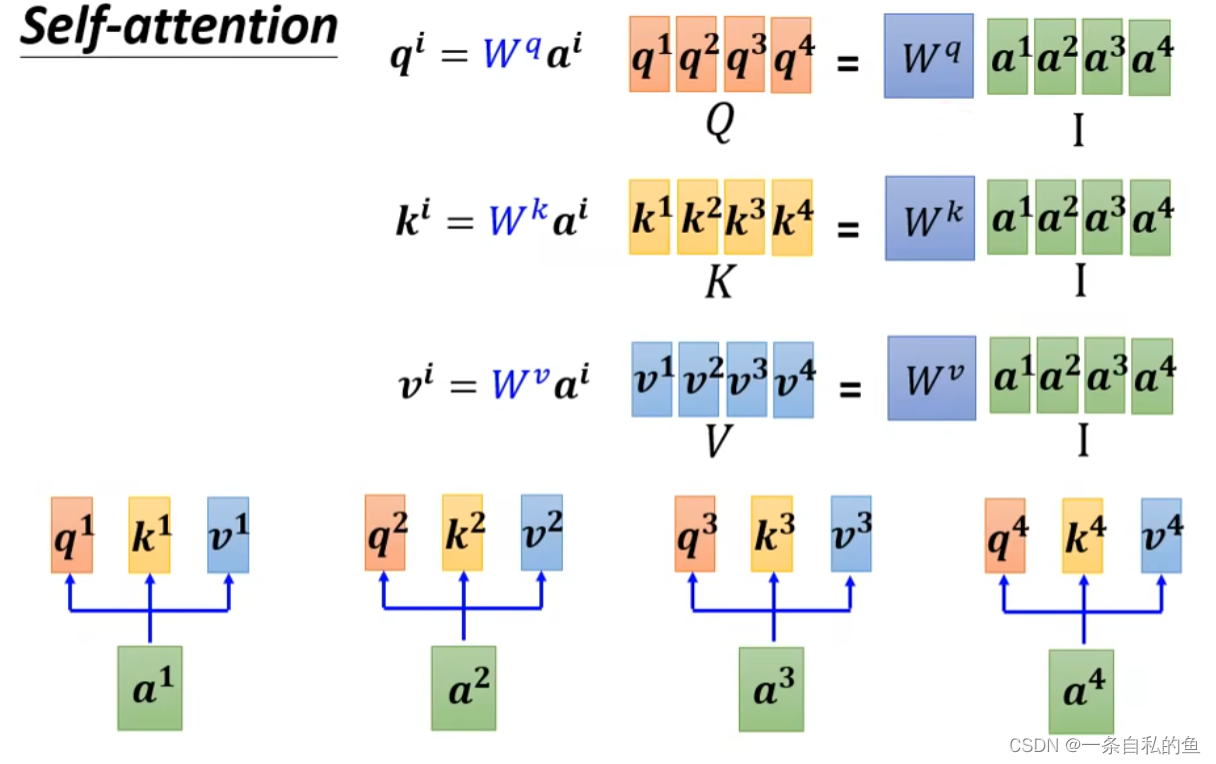
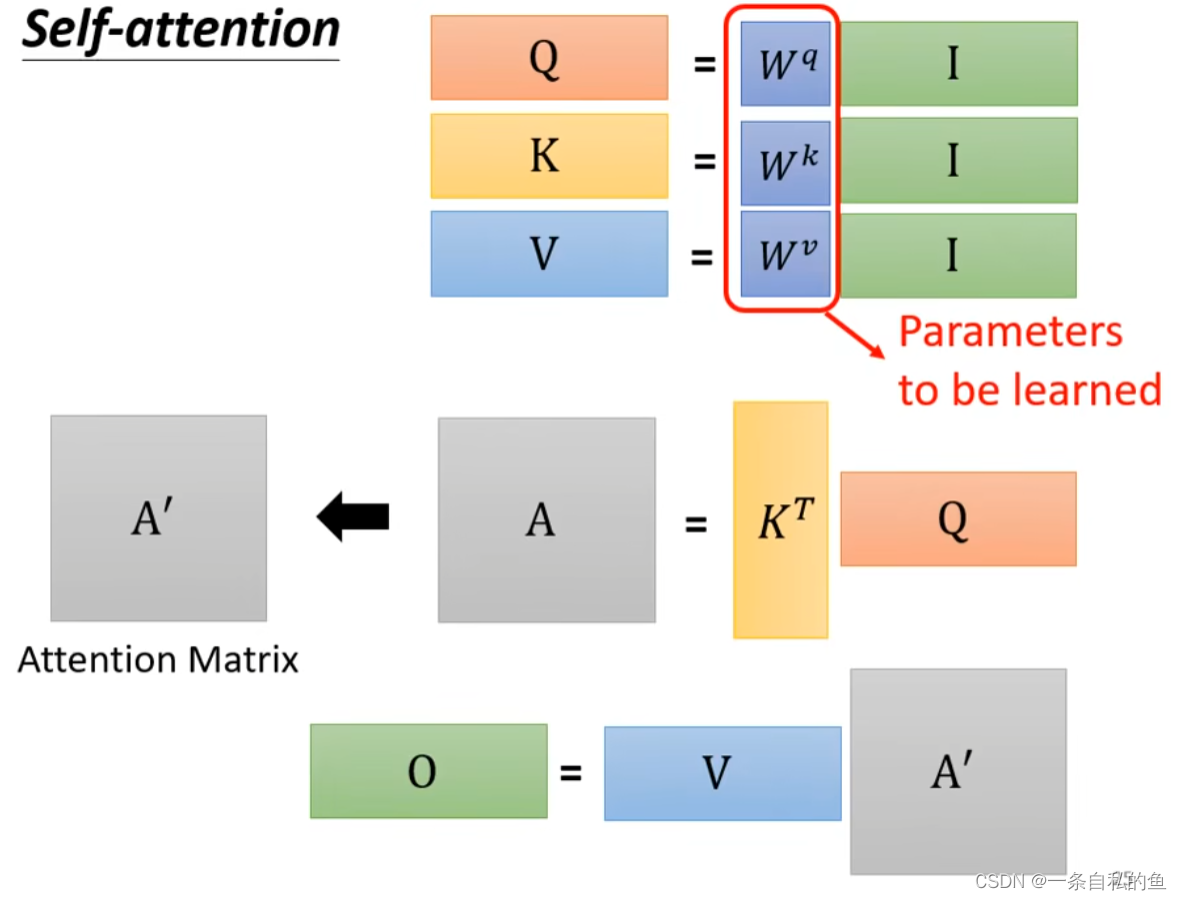
对于每一个向量a1、a2等,我们都需要计算出它相对应的q1、k1和v1,如果我们把a1、a2、a3和a4连起来变成一个矩阵I,然后用矩阵W乘上这个矩阵I就可以得到一个Q的矩阵,这个矩阵其实就是q1、q2、q3和q4连起来,同理我们也同样用矩阵I乘上变成k的矩阵Wk,就可以变成矩阵K,矩阵V同理,如下图
然后考虑如何计算出关联性α矩阵,对于a1要计算所有向量跟他的关联性,其实就是用q1乘上所有向量的k值,我们把k列起来再乘q得出的结果就是关于a1的关联性的一列值,同理在q1的后面带上q2、q3和q4则依次可以得到a2、a3和a4他们的关联性矩阵,最后再用softmax这个方法进行normalization,softmax也可以用其他方法,比如RELU

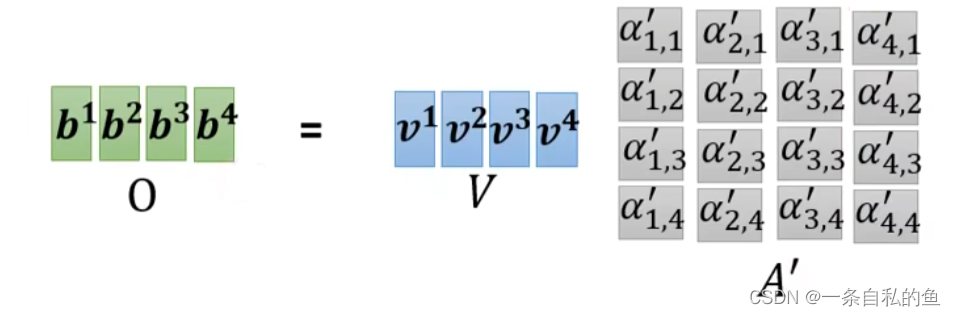
最后对于每一个向量a的输出b,也就是用各自的v乘上每一个这两个向量的关联性α再相加,其实就是下图的矩阵乘法
回顾整个self-attention自注意力机制,其实就是一直做矩阵乘法,我们整个过程需要学习的只有三个W矩阵,这三个矩阵是输入I相乘得到Q、K和V的矩阵
多头自注意力机制 multi-head self-attention
如果两个向量不止有一种关系,这时我们就需要用multi-head self-attention,也就是多头自注意力机制,也就是对于Q、K、V这三个矩阵我们可以再乘上一个矩阵变成多部分矩阵,比如如果有两个heads,那么我们可以把Q这个矩阵乘上一个矩阵变成q1、q2,W和V同理
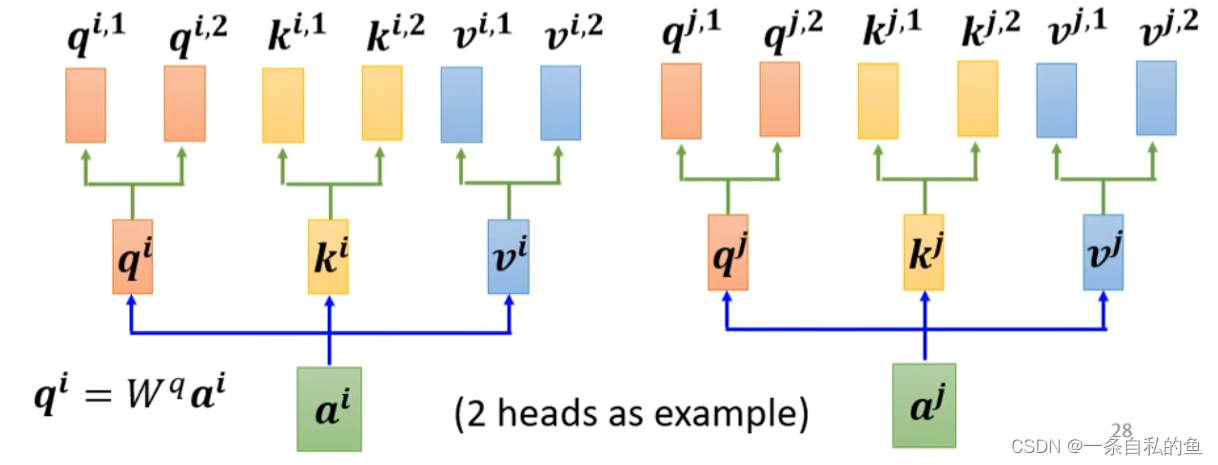
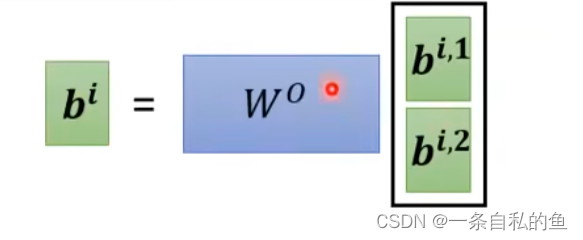
其他的操作和上面是一致的,我们只需要对每一部分的Q、K、V做矩阵运算,最后会得出多个结果b,将这多个结果排列起来然后再乘上一个矩阵变成一个结果即可
positional encoding 位置编码
我们可以给每一个ai加上一个ei表明这个更可能是哪个位置,ei是人为设置的,也可以从数据中学习获得
truncated self-attention
设想语音识别的一种情况,对于声音的每20ms我们都作为一段向量,那么1s会有50个向量,而这50个向量将会有一个50x50的关联性矩阵,计算起来将非常的繁琐,如果语音的时间更长,那么将会有更加庞大的矩阵非常难以计算,因为这需要我们有一个非常大的一个memory和比较长的时间
如何解决上述问题呢,答案就是不要看一整段那么长,我们只取跟当前向量相邻的几个向量计算即可,当然这个范围是人为设置的
softmax函数
通常日常生活中我们求最大值都是求得hardmax,也就是固定的,也就是非黑即白,但是在人工智能领域这种方式是不合情理的,比如对于文本分类来说,一篇文章或多或少包含着各种主题信息,我们更期望得到文章对于每个可能的文本类别的概率值(置信度),可以简单理解成属于对应类别的可信度。所以此时用到了soft的概念,Softmax的含义就在于不再唯一的确定某一个最大值,而是为每个输出分类的结果都赋予一个概率值,表示属于每个类别的可能性。
softmax函数的定义如下,也就是对于每一个输入我们都用e的多少次方除以总和的值代表
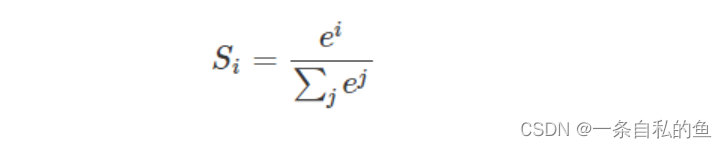
优点:使用指数形式的Softmax函数能够将差距大的数值距离拉的更大
缺点:值非常大的时侯可能数值溢出