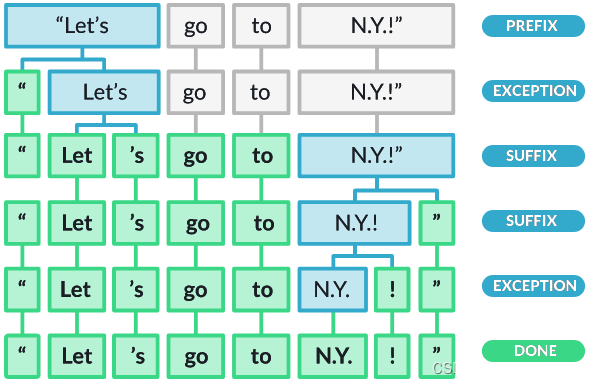
问题

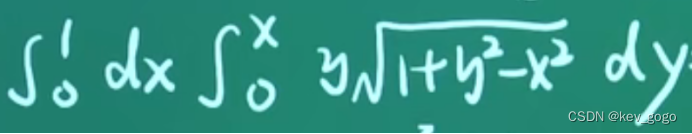
在做这个积分的时候，产生了一个疑问，就是这个积分中，第一次积分能将x视为常数已经成为一个下意识的动作了，然而，是否能够真的将积分中的x看作常数？而这个积分限上也有一个x，这个积分限上的x和函数内部的x是否有区别？

思考

在定积分中，我们知道一个定积分就是以f(x)为高度，对x轴积分，积得的一个面积。
在二重积分中，实际上也有几何意义，就是一个曲顶柱体的体积。

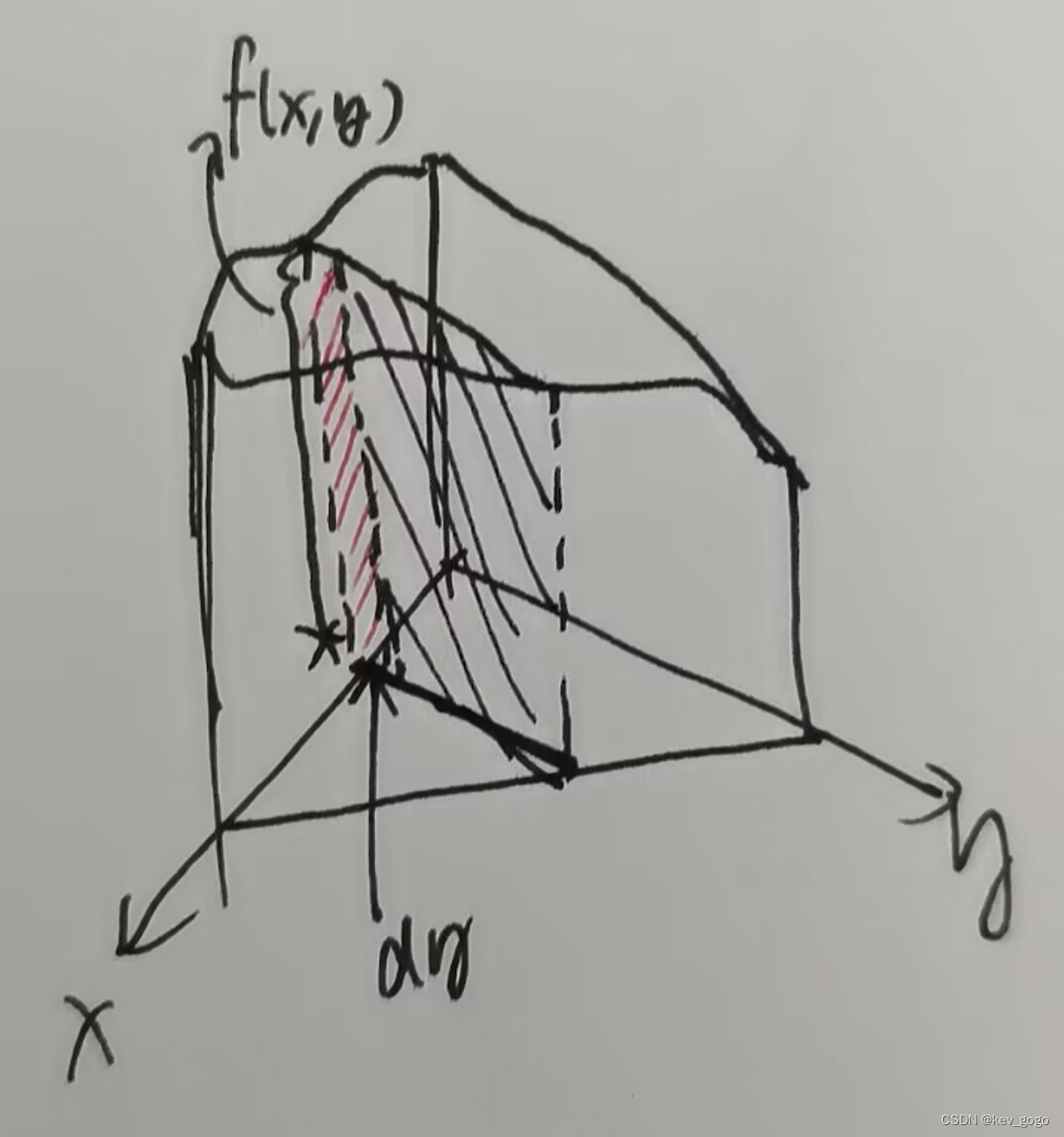
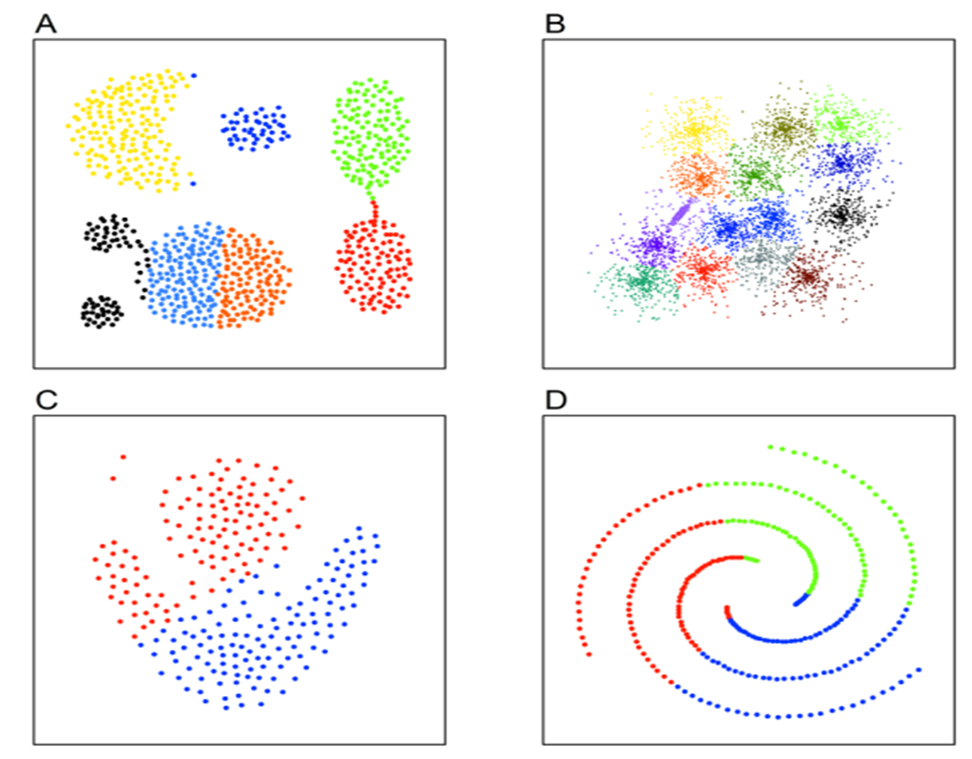
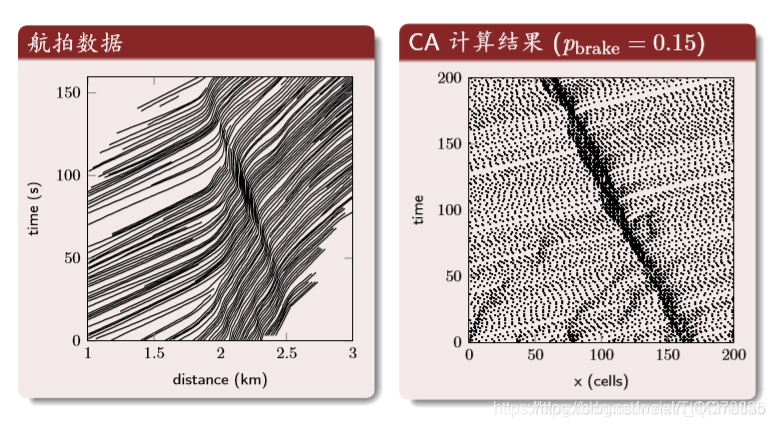
这张图片不是原文对应的函数区域（实在不会画了）。

可以看到，我们的二重积分积分区域就是底面，对于每一个点的高度就是f(x,y)，二重积分的过程就是（以先y后x为例）先用一个定积分积出来一个面积，再用一个定积分将无数个面摞成一个体。（就像定积分中先指出一个线，再把无数条线摞成一个面，就是一维到二维，二维到三维）

而在第一重函数积分的时候，一定是固定一个x，因为如果x也在变的话，第一重函数积分积出来的就不是面了，而是体了，不符合一重积分的定义。

因此，这个函数里的x和积分限上的x是一个x，也就是在第一重积分中x可以看做是一个常数。