【元胞自动机】元胞自动机短消息网络病毒传播仿真【含Matlab源码 1289期】

⛄一、元胞自动机简介

1 元胞自动机发展历程
最初的元胞自动机是由冯 · 诺依曼在 1950 年代为模拟生物细胞的自我复制而提出的. 但是并未受到学术界重视.
1970 年, 剑桥大学的约翰 · 何顿 · 康威设计了一个电脑游戏 “生命游戏” 后, 元胞自动机才吸引了科学家们的注意.

1983 年 S.Wolfram 发表了一系列论文. 对初等元胞机 256 种规则所产生的模型进行了深入研究, 并用熵来描述其演化行为, 将细胞自动机分为平稳型, 周期型, 混沌型和复杂型.

2 对元胞自动机的初步认识
元胞自动机（CA）是一种用来仿真局部规则和局部联系的方法。典型的元胞自动机是定义在网格上的，每一个点上的网格代表一个元胞与一种有限的状态。变化规则适用于每一个元胞并且同时进行。典型的变化规则，决定于元胞的状态，以及其（ 4 或 8 ）邻居的状态。

3 元胞的变化规则&元胞状态
典型的变化规则，决定于元胞的状态，以及其（ 4 或 8 ）邻居的状态。

4 元胞自动机的应用
元胞自动机已被应用于物理模拟，生物模拟等领域。

5 元胞自动机的matlab编程
结合以上，我们可以理解元胞自动机仿真需要理解三点。一是元胞，在matlab中可以理解为矩阵中的一点或多点组成的方形块，一般我们用矩阵中的一点代表一个元胞。二是变化规则，元胞的变化规则决定元胞下一刻的状态。三是元胞的状态，元胞的状态是自定义的，通常是对立的状态，比如生物的存活状态或死亡状态，红灯或绿灯，该点有障碍物或者没有障碍物等等。

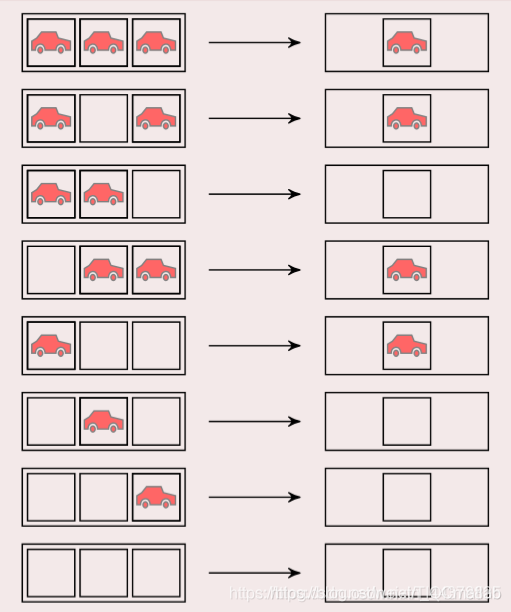
6 一维元胞自动机——交通规则
定义：
6.1 元胞分布于一维线性网格上.
6.2 元胞仅具有车和空两种状态.
在这里插入图片描述
7 二维元胞自动机——生命游戏
定义：
7.1 元胞分布于二维方型网格上.
7.2 元胞仅具有生和死两种状态.

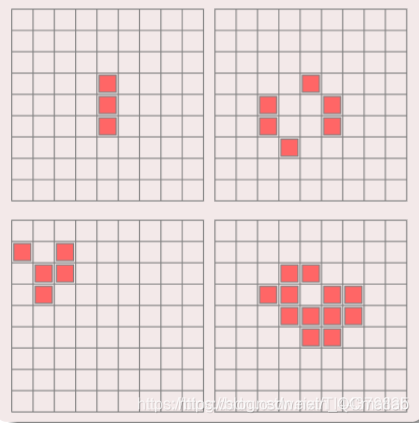
元胞状态由周围八邻居决定.
规则：

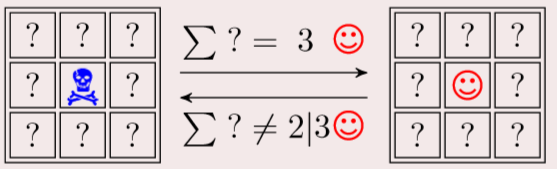
骷髅：死亡；笑脸：生存
周围有三个笑脸，则中间变为笑脸
少于两个笑脸或者多于三个，中间则变死亡。

8 什么是元胞自动机
离散的系统: 元胞是定义在有限的时间和空间上的, 并且元胞的状态是有限.
动力学系统: 元胞自动机的举止行为具有动力学特征.
简单与复杂: 元胞自动机用简单规则控制相互作用的元胞模拟复杂世界.

在这里插入图片描述
9 构成要素

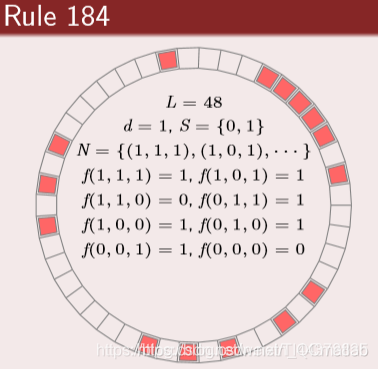
（1）元胞 (Cell)

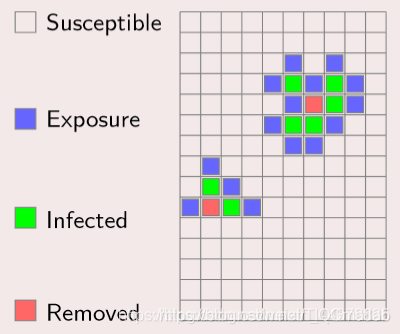
元胞是元胞自动机基本单元：
状态: 每一个元胞都有记忆贮存状态的功能.
离散: 简单情况下, 元胞只有两种可能状态; 较复杂情况下, 元胞具有多种状态.
更新: 元胞的状态都安照动力规则不断更新.
（2）网格 (Lattice)
不同维网格
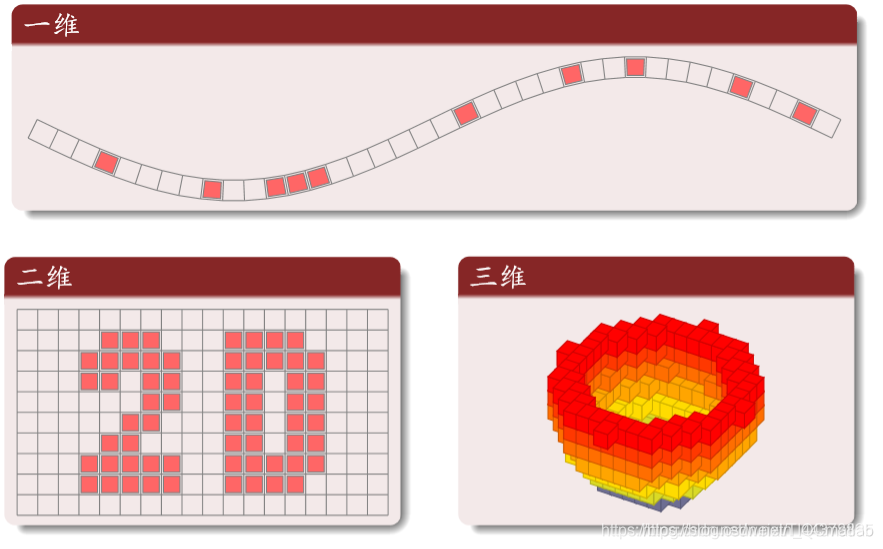
在这里插入图片描述
常用二维网格

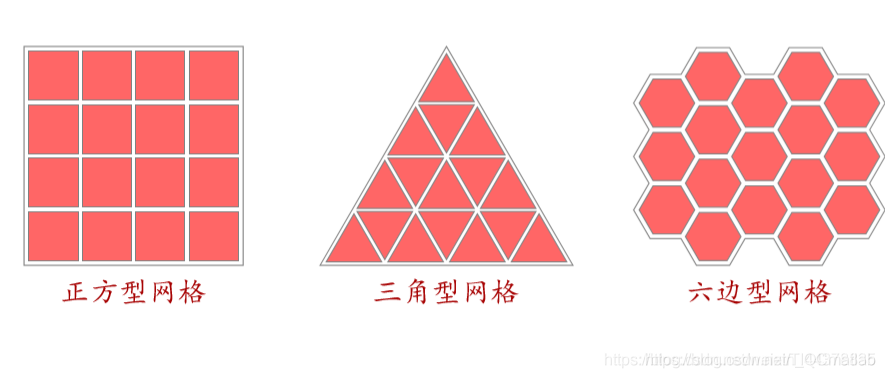
（3）邻居 (Neighborhood)

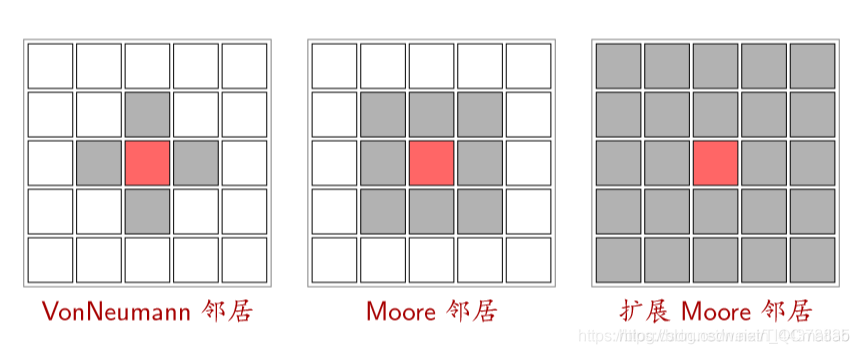
（4）边界 (Boundary)

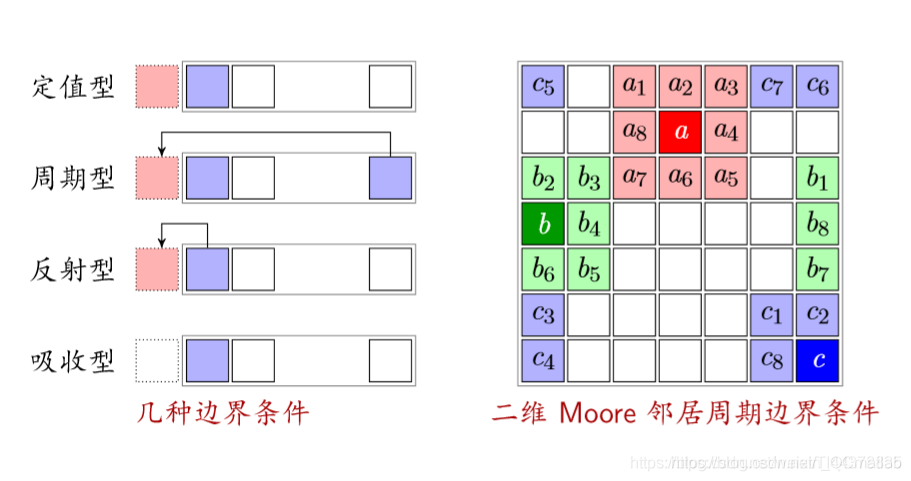
反射型：以自己作为边界的状态
吸收型：不管边界（车开到边界就消失）

（5）规则（状态转移函数）
定义：根据元胞当前状态及其邻居状况确定下一时刻该元胞状态的动力学函数, 简单讲, 就是一个状态转移函数.
分类：
总和型: 某元胞下时刻的状态取决于且仅取决于它所有邻居的当前状态以及自身的当前状态.
合法型: 总和型规则属于合法型规则. 但如果把元胞自动机的规则限制为总和型, 会使元胞自动机具有局限性.
（6）森林火灾
在这里插入图片描述
绿色：树木；红色：火；黑色：空地。
三种状态循环转化：
树：周围有火或者被闪电击中就变成火。
空地：以概率p变为树木
理性分析：红为火；灰为空地；绿是树

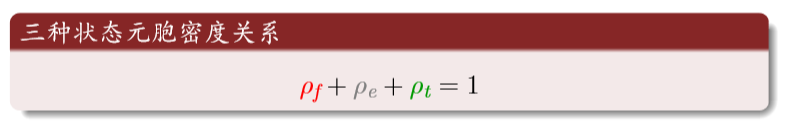
元胞三种状态的密度和为1

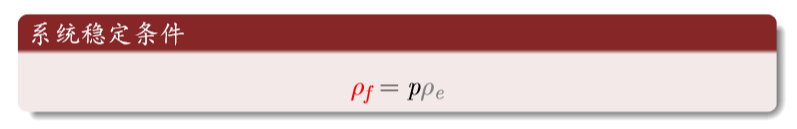
火转化为空地的密度等于空地转换为树的密度（新长出来的树等于烧没的树）
在这里插入图片描述
f是闪电的概率:远远小于树生成的概率；T s m a x T_{smax}T smax
是一大群树被火烧的时间尺度
程序实现
周期性边界条件
购进啊

其中的数字为编号
构建邻居矩阵

上面矩阵中的数字编号，对应原矩阵相同位置编号的上邻居编号，一一对应
同样道理：
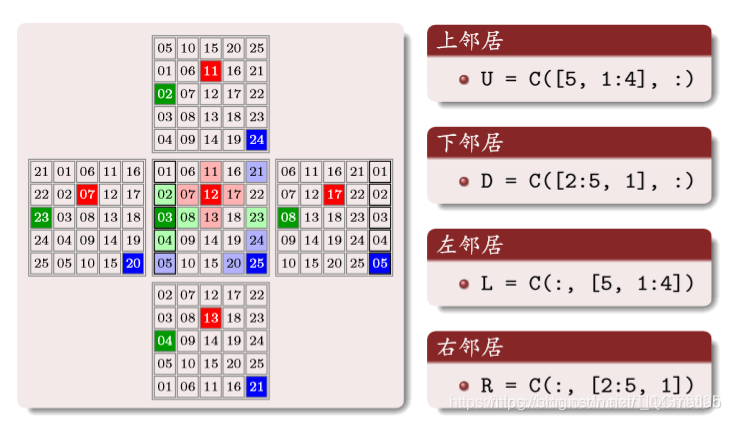
在这里插入图片描述
（7）交通概念
车距和密度

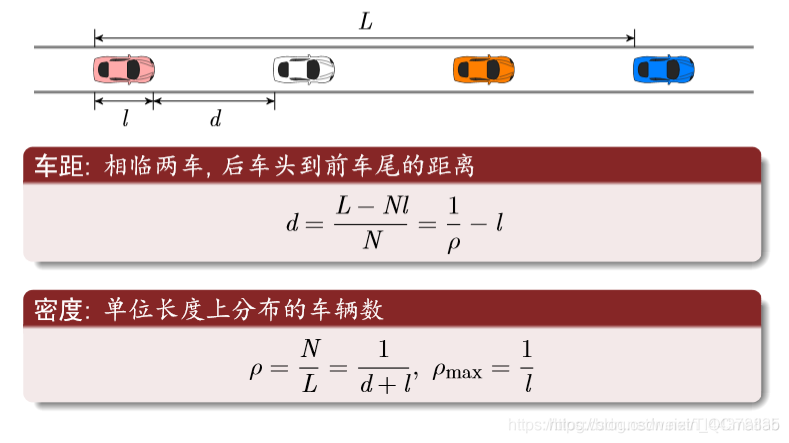
流量方程

守恒方程

时空轨迹（横轴是空间纵轴为时间）

红线横线与蓝色交点表示每个时间车的位置。
如果是竖线则表示车子在该位置对应的时间

宏观连续模型：
在这里插入图片描述
最常用的规则：

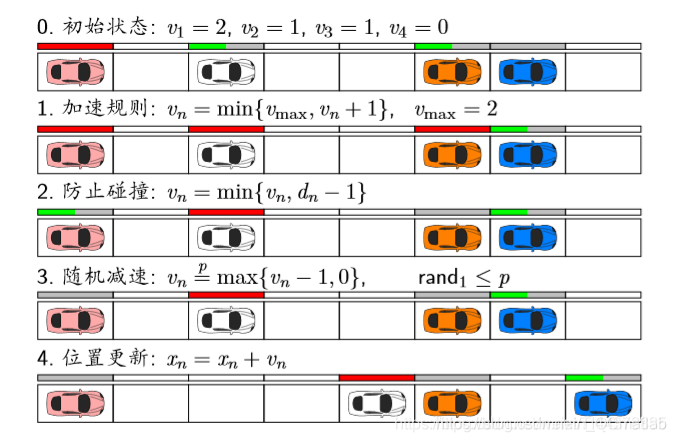
红色条表示速度是满的。

1 加速规则：不能超过v m a x （ 2 格 / s ） v_{max}（2格/s）v
max（2格/s）
2 防止碰撞：不能超过车距

理论分析：
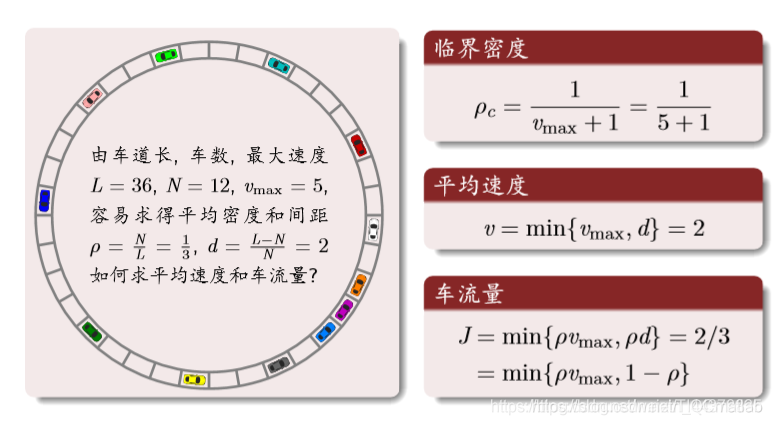
在这里插入图片描述
结果分析: 密度与流量

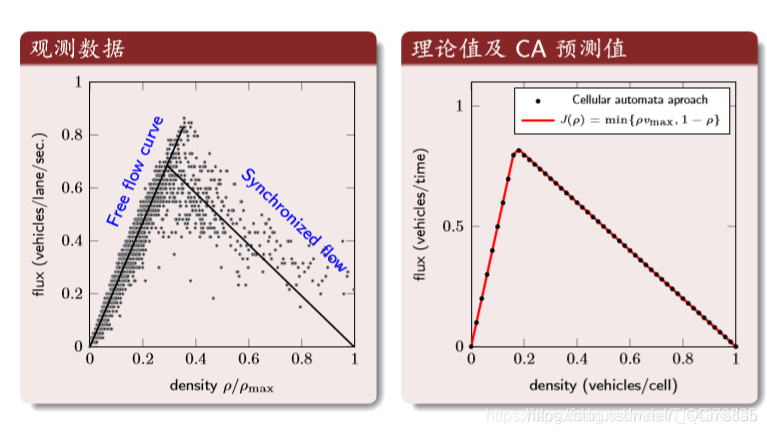
第一个图：横坐标是归一化后的密度，纵坐标是车流量。第二个图：理论值与CA的结果

结果分析: 时空轨迹
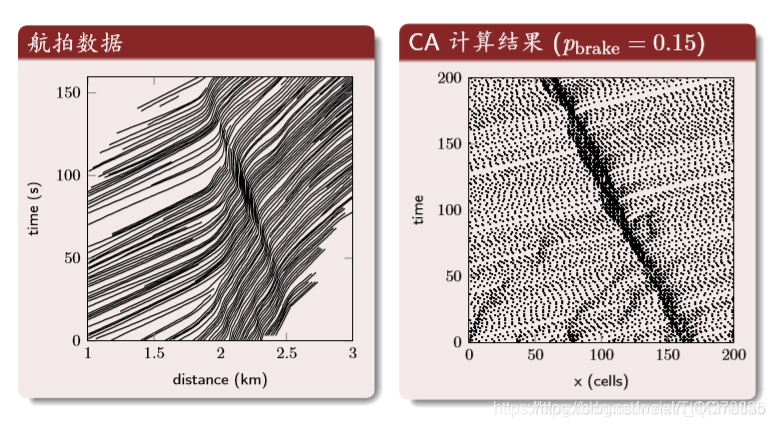
在这里插入图片描述
中间的深色区域是交通堵塞的区域。

⛄二、部分源代码

function Message_Spread_Mode
tic
load '.\Data\Link.txt';    %读入连接矩阵
% load 'C:\Users\user\Desktop\基于元胞自动机的短信网络病毒传播模拟\Data\Point_X.txt'; %读入横坐标
% load 'C:\Users\user\Desktop\基于元胞自动机的短信网络病毒传播模拟\Data\Point_Y.txt'; %读入纵坐标
%-------------------------------------------------------------------------%
%状态分布及状态转移概率SEIR
%0:易感状态S（Susceptible）  P_0_1; （P_0_3:预免疫系数）
%1:潜伏状态E（Exposed）      P_1_0；  P_1_2；P_1_3
%2:染病状态I（Infected）     P_2_0；  P_2_3
%3:免疫状态R（Recovered）    P_3_0
%-------------------------------------------------------------------------%
%计算各用户节点的度                                                          
De=sum(Link);                                                              %用户节点的度
%------------——————----参数设置与说明--------------------------------%
[M N]=size(Link);                                                          %连接矩阵的规模
I_E=0.6;                                                                   %潜伏期E用户的传染强度
I_I=0.9;                                                                   %发病期I用户的传染强度
lamda=sum(De)/M;                                                           %手机用户单位时间内平均发送信息的数量
%P_m1： 手机用户预免疫系数
%State：手机用户所处状态State=zeros(1,M);0:表示易感状态（Susceptible）
%---------------------------------1---------------------------------------%
%先讨论用户预免疫系数P_m1对病毒传播的影响
TimeStep=50;%input('短信网络内病毒传播模拟时间：');
P_m1=[0.1,0.5,0.9];         %用户预免疫系数
% State=zeros(TimeStep,M);  %手机用户的状态  
G_t=5;                      %G_t：手机用户的免疫持续时间，反映了病毒的变异频率
F_t=5;                      %F_t：手机用户从发现病毒到杀毒并升级病毒库的时间
for i=1:length(P_m1)
    TimeLong_F=zeros(1,M); %用户处于染病期的时间长短
    TimeLong_E=zeros(1,M); %用户处于潜伏期的时间长短
    Sta=zeros(1,M);                                                      %手机用户的状态 
    %进行预免疫设定
    for j=1:M
        if rand(1)<=P_m1(i)
            Sta(j)=3;         %进入免疫状态
            TimeLong_E(j)=1;  %出入潜伏期的时间为1
        else
            continue;
        end
    end
    %状态转换
    %初始随机选择一个节点为病源点（此时不能选处于免疫状态的点）
    %问题：节点度大小存在差别，可能模拟出来的结果有出于
    %      为避免这个问题，我们取度最大的节点为病源节点，如果已免疫，则选次大的，一次下去
    [Number,Sta]=Select_Infected_Point(M,Sta,De);
    %Number：病源节点
    %State ：确定病源节点以后的节点状态矩阵
    State=zeros(TimeStep,M);
    Number_State=zeros(4,TimeStep);  %用户处于个状态的统计数量
    for t=1:TimeStep
        if t==1
            State(t,:)=Sta;
        else
            %模拟每个用户节点的状态
            for j=1:M
                %判断用户节点处于什么状态，然后根据其状态确定其转变情况
                if State(t-1,j)==0                          %此时处于易感状态0，可能向潜伏期转移
                    Num=Select_Number_Near(j,Link);         %找出节点j的邻居节点
                    P=zeros(1,length(Num));                 %邻居节点感染该节点的概率
                    for k=1:length(Num)
                        if State(t-1,Num(k))==1             %节点处于潜伏期E（1）
                            P(k)=I_E/De(Num(k))*sum((lamda.^([1:De(Num(k))]).*exp(-lamda))./...
                                (factorial([1:De(Num(k))]-1)));
                        else
                            if State(t-1,Num(k))==2          %节点处于染病期I（2）
                                P(k)=I_I/De(Num(k))*sum((lamda.^([1:De(Num(k))]).*exp(-lamda))./(factorial([1:De(Num(k))]-1)));
                            else
                                continue;
                            end
                        end
                    end
                    P_0_1=max(P);                       %节点感染病毒的概率
                    if rand<=P_0_1                      %此时节点进入潜伏期
                       State(t,j)=1;
                    else
                       State(t,j)=State(t-1,j); 
                    end
                else
                    if State(t-1,j)==1         %此时处于潜伏状态E，可能向易感S，染病I和免疫R转移
                        if rand<=1/(1+exp(-De(j)))                 %向染病状态I转移                
                            State(t,j)=2;
                            TimeLong_F(j)=TimeLong_F(j)+1;         %用户j处于染病状态的时间长短  
                        else
                            if rand<=1/(1+exp(-De(j)))             %向易感状态S转移           
                                State(t,j)=0;
                            else
                                if rand<=1/(1+exp(-De(j)))         %向免疫状态R转移
                                    State(t,j)=3;
                                    TimeLong_E(j)=TimeLong_E(j)+1; %免疫时间增加1
                                else
                                    State(t,j)=State(t-1,j);       %状态不变，依然为潜伏期E（1）
                                end
                            end
                        end
                    else
                        if State(t-1,j)==2        %此时处于欺染病状态I，可能向易感S，免疫R转移
                            if TimeLong_F(j)<=F_t         %表示此时用户不对手机病毒进行任何处理
                                State(t,j)=State(t-1,j);           %此时手机用户维持在原状态I
                                TimeLong_F(j)=TimeLong_F(j)+2;
                            else
                                %此时手机用户对手机进行杀毒并升级病毒库，进入免疫状态R
                                State(t,j)=3;
                                TimeLong_F(j)=0; %处于感染期（中毒状态）的时间长度
                                TimeLong_E(j)=1; %进入免疫期的时间长度
                            end
                        else
                            %此时手机用户处于免疫期
                            if TimeLong_E<=G_t   %病毒此时并未突变，维持原状态R（免疫状态）
                                State(t,j)=State(t-1,j);
                                TimeLong_E(j)=TimeLong_E(j)+1; %处于免疫期的时间增加
                            else
                                if rand<=1/G_t  %病毒突变，状态转移为易感状态S
                                    State(t,j)=0;
                                    TimeLong_E(j)=0;
                                else
                                    %此时用户状态依然不变
                                    State(t,j)=State(t-1,j);
                                    TimeLong_E(j)=TimeLong_E(j)+1; %处于免疫期的时间增加
                                end
                            end
                        end
                    end
                end
            end
        end
        %统计各状态的节点数量
        Number_State(1,t)=sum(State(t,:)==0);%处于易感状态S的总节点数量
        Number_State(2,t)=sum(State(t,:)==1);%处于易感状态E的总节点数量
        Number_State(3,t)=sum(State(t,:)==2);%处于易感状态I的总节点数量
        Number_State(4,t)=sum(State(t,:)==3);%处于易感状态R的总节点数量
        figure(i)
        if rem(t,3)==0
            plot([t-1 t],[Number_State(1,t-1) Number_State(1,t)],'md-'),hold on
            plot([t-1 t],[Number_State(2,t-1) Number_State(2,t)],'gh:'),hold on
            plot([t-1 t],[Number_State(3,t-1) Number_State(3,t)],'bs-.'),hold on
            plot([t-1 t],[Number_State(4,t-1) Number_State(4,t)],'k.-'),hold on
        else
            continue;
        end
        legend('易感状态Susceptible','潜伏状态Exposed','染病状态Infected','免疫状态Recovered')
        xlabel('模拟时间')
        ylabel('各状态的手机用户数量')
    end
end
P_m1=0.3;         %用户预免疫系数
% State=zeros(TimeStep,M);  %手机用户的状态  
% G_t=5;                      %G_t：手机用户的免疫持续时间，反映了病毒的变异频率
G_t=[1,5,9];
F_t=5;                      %F_t：手机用户从发现病毒到杀毒并升级病毒库的时间
for i=1:length(G_t)
    TimeLong_F=zeros(1,M); %用户处于染病期的时间长短
    TimeLong_E=zeros(1,M); %用户处于潜伏期的时间长短
    Sta=zeros(1,M);                                                      %手机用户的状态 
    %进行预免疫设定
    for j=1:M
        if rand(1)<=P_m1
            Sta(j)=3;         %进入免疫状态
            TimeLong_E(j)=1;  %出入潜伏期的时间为1
        else
            continue;
        end
    end
    %状态转换
    %初始随机选择一个节点为病源点（此时不能选处于免疫状态的点）
    %问题：节点度大小存在差别，可能模拟出来的结果有出于
    %      为避免这个问题，我们取度最大的节点为病源节点，如果已免疫，则选次大的，一次下去
    [Number,Sta]=Select_Infected_Point(M,Sta,De);
    %Number：病源节点
    %State ：确定病源节点以后的节点状态矩阵
    State=zeros(TimeStep,M);
    Number_State=zeros(4,TimeStep);  %用户处于个状态的统计数量
    for t=1:TimeStep
        if t==1
            State(t,:)=Sta;
        else
            %模拟每个用户节点的状态
            for j=1:M
                %判断用户节点处于什么状态，然后根据其状态确定其转变情况
                if State(t-1,j)==0                          %此时处于易感状态0，可能向潜伏期转移
                    Num=Select_Number_Near(j,Link);         %找出节点j的邻居节点
                    P=zeros(1,length(Num));                 %邻居节点感染该节点的概率
                    for k=1:length(Num)
                        if State(t-1,Num(k))==1             %节点处于潜伏期E（1）
                            P(k)=I_E/De(Num(k))*sum((lamda.^([1:De(Num(k))]).*exp(-lamda))./...
                                (factorial([1:De(Num(k))]-1)));
                        else
                            if State(t-1,Num(k))==2          %节点处于染病期I（2）
                                P(k)=I_I/De(Num(k))*sum((lamda.^([1:De(Num(k))]).*exp(-lamda))./...
                                    (factorial([1:De(Num(k))]-1)));
                            else
                                continue;
                            end
                        end
                    end
                    P_0_1=max(P);                       %节点感染病毒的概率
                    if rand<=P_0_1                      %此时节点进入潜伏期
                       State(t,j)=1;
                    else
                       State(t,j)=State(t-1,j); 
                    end
                else
                    if State(t-1,j)==1          %此时处于潜伏状态E，可能向易感S，染病I和免疫R转移
                        if rand<=1/(1+exp(-De(j)))                 %向染病状态I转移                
                            State(t,j)=2;
                            TimeLong_F(j)=TimeLong_F(j)+1;         %用户j处于染病状态的时间长短  
                        else
                            if rand<=1/(1+exp(-De(j)))             %向易感状态S转移           
                                State(t,j)=0;
                            else
                                if rand<=1/(1+exp(-De(j)))         %向免疫状态R转移
                                    State(t,j)=3;
                                    TimeLong_E(j)=TimeLong_E(j)+1; %免疫时间增加1
                                else
                                    State(t,j)=State(t-1,j);       %状态不变，依然为潜伏期E（1）
                                end
                            end
                        end
                    else
                        if State(t-1,j)==2           %此时处于欺染病状态I，可能向易感S，免疫R转移
                            if TimeLong_F(j)<=F_t          %表示此时用户不对手机病毒进行任何处理
                                State(t,j)=State(t-1,j);           %此时手机用户维持在原状态I
                                TimeLong_F(j)=TimeLong_F(j)+2;
                            else
                                %此时手机用户对手机进行杀毒并升级病毒库，进入免疫状态R
                                State(t,j)=3;
                                TimeLong_F(j)=0; %处于感染期（中毒状态）的时间长度
                                TimeLong_E(j)=1; %进入免疫期的时间长度
                            end
                        else
                            %此时手机用户处于免疫期
                            if TimeLong_E<=G_t(i)   %病毒此时并未突变，维持原状态R（免疫状态）
                                State(t,j)=State(t-1,j);
                                TimeLong_E(j)=TimeLong_E(j)+1; %处于免疫期的时间增加
                            else
                                if rand<=1/G_t(i)              %病毒突变，状态转移为易感状态S
                                    State(t,j)=0;
                                    TimeLong_E(j)=0;
                                else
                                    %此时用户状态依然不变
                                    State(t,j)=State(t-1,j);
                                    TimeLong_E(j)=TimeLong_E(j)+1; %处于免疫期的时间增加
                                end
                            end
                        end
                    end
                end
            end
        end
     
 
## ⛄三、运行结果
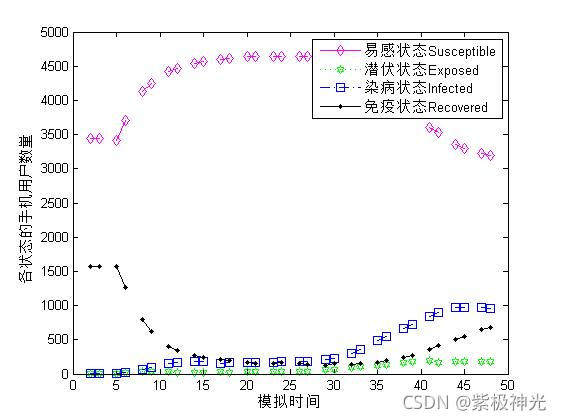
![在这里插入图片描述](https://img-blog.csdnimg.cn/2b76fa72d3ce4d679bb162f11ca91ae4.jpg?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBA57Sr5p6B56We5YWJ,size_19,color_FFFFFF,t_70,g_se,x_16#pic_center)


## ⛄四、matlab版本及参考文献
**1 matlab版本**
2014a

**2 参考文献**
[1]党珊,蒋太刚,巫承军.基于元胞自动机方法的消防疏散仿真研究[J].现代电子技术. 2022,45(21)
[2]帅斌,秦梦瑶,许旻昊.基于元胞自动机的高速铁路列车运行仿真研究[J].计算机仿真. 2022,39(08)
[3]张睿洋.元胞自动机在两类传染病模型中的应用[J].现代信息科技. 2022,6(10)

**3 备注**
简介此部分摘自互联网，仅供参考，若侵权，请联系删除