Clustering by Fast Search and Find of Density Peaks(CFDP)  - 发表于2014 science期刊

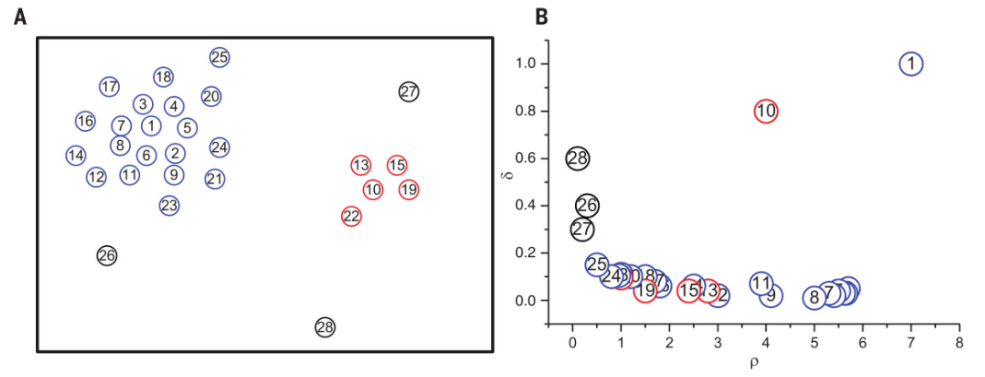
聚类算法，作为机器学习里常用的一种无监督方法，一直以来都受到很大的关注。聚类算法，是希望把同一类的样本或者样本聚到一起，比如说常见的图像分类，我们希望猫的图片能聚到一起，狗的图片能聚到一起，不希望猫和狗的图片混在一起。经典的聚类算法K-means是通过指定聚类中心，再通过迭代的方式更新聚类中心的方式，由于每个点都被指派到距离最近的聚类中心，所以导致其不能检测非球面类别的数据分布。虽然有DBSCAN（density-based spatial clustering of applications with noise）对于任意形状分布的进行聚类，但是必须指定一个密度阈值，从而去除低于此密度阈值的噪音点。

该算法假设：

1. 聚类中心周围都是密度比其低的点；

2. 这些点距离该聚类中心的距离相比于其他聚类中心来说是最近的。

CFDP算法就是基于这两个假设来识别和查找聚类中心：

1、局部密度：

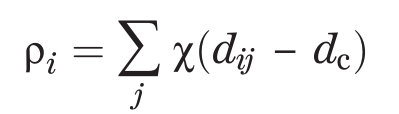
已知任意两点 i 和 j 间的距离的度量为dij

• dc为参数，用来体现邻域的大小；

• ρi越大表示点 i 局部密度越大，越有可能成为聚类中心。

2、相对距离：

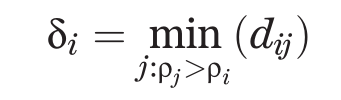
• δi 表示密度大于点 i 的点中到点i的最小距离，该值越大，表示点 i 距离高密度点的距离越远，则点 i 越有可能成为聚类中心；

• 如果点 i 的密度为全局最大，则令δi的值为到点 i 的最大距离。

根据上述步骤，我们已经求的了样本点距离向量和密度向量。根据公式，将距离值和密度值综合考虑：

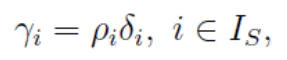
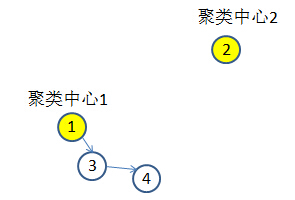
将点成得到大小为mx1的向量记为score，将score从大到小排序后，若需要N个聚类，则从score中取出前N个点作为聚类中心。如下图，得到聚类中心1、10。

当聚类中心确定之后，就要为m个样本点分配它们所属的类别了：

例如4样本点的上级是3，那么我们需要去寻找3的上级是谁，得到3的上级是1且为聚类中心，那么就停止寻找。此时4的类别就是1了。所以最终得到下图类别所属向量里面的元素只有1和2。

下面就是该算法最让我惊艳的部分了，它可以自动筛出噪点，无需人为设置阈值，更加的“自动化”。

在对每一个点指派所属类别之后，该算法并没有人为的直接用噪音信号截断的方法去除噪音点，而是先算出类别之间的边界，然后找出边界中密度值最高的点的密度作为阈值，只保留前类别中大于或等于此密度值的点。

首先为每个类簇定义一个边界区域，即分配到该类簇但于其它类簇的点的距离小于dc（截断距离）的点的集合。然后为每个类簇找到其边界区域中密度最高的点，并以该点的密度作为阀值来筛选类簇。

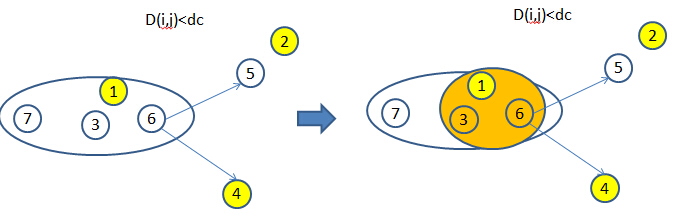
以下图为例，对于类别1中的所有点（1，3，6，7），计算与其他类别中所有点距离小于等于截断距离DC的最大密度值，例如“1”号点由于其距离其他类别的点的距离均大于DC，因此不予考虑。由下图可以看出密度第6的值距离其他类别最近所以选定密度=(6)，由于“7”号点的密度(7)<（6）， 因此将其作为噪音点去除，最后得到的类别1的点为橙色圈所示“1”、“3”和“6”。

最后做个总结：

找到聚类中心后，对每一个点进行簇的归属，相比其他的算法，CFDP不需要迭代计算，要远低于K-means算法的复杂度。

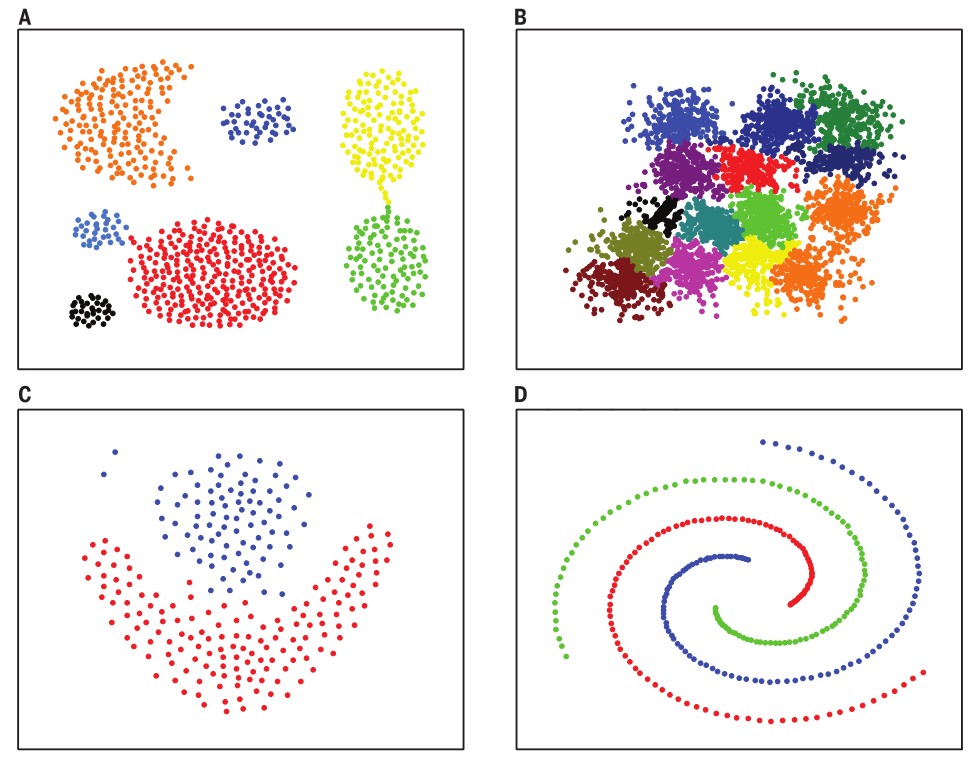
算法可以得到非球形的聚类结果，很好地描述数据分布。左图为CFDP结果，右图为K-MEANS结果，迭代10000步。K-means方法是在使用了正确的K值的条件进行优化。在大多数情况下，聚类结果都不符合视觉结果。而CFDP算法能适应各种不规则的数据分布

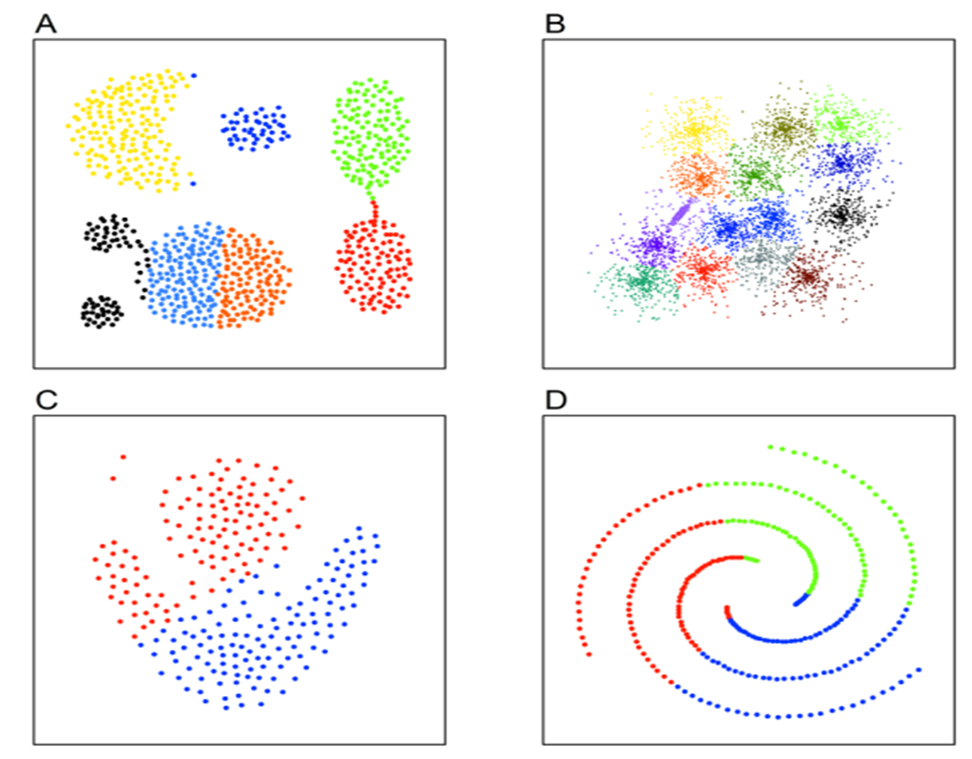
但是CFDP需要事先计算好所有点与点之间的距离，如果样本太大则整个距离矩阵的内存开销特别大。如果只需要得到最终聚类中心，则可以考虑牺牲速度的方式计算每一个样本点的和，避免直接加载距离矩阵。

大家有更好的想法欢迎到评论区留言互动~