[小全读书笔记] 从问题和公式角度理解 Diffusion Model
- 1. Diffusion Model的结构
- 1.1 定义与限制
- 1.2 定义与限制的数学体现
- 2. Diffusion Model的模型训练
- 2.1 似然函数转换成ELBO
- 2.2 拆解ELBO
- 2.3 求解关键: q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0)的显示表达
- 3. 附录
- 3.1 最大化似然函数
此读书笔记本意是想理解文章 Denoising Diffusion Probabilistic Models (DDPM),但确实因为里边提到的公式对于跨领域读者有点晦涩难懂,但写者又希望能稍微从公式角度去理解其背后原理,写者进一步借助文章Understanding Diffusion Models: A Unified Perspective进行理解,因此本文主要记录了在阅读和理解后一篇文章的心路历程。
本文会省略掉一些关于模型背景等方面的介绍,而主要集中于理解背后公式的出发点和直观解释。
1. Diffusion Model的结构

Diffusion Model的目标是学习一套模型,能将噪声
x
T
x_T
xT还原成原始图片
x
0
x_0
x0的一套模型,而整个模型的结构包含了两部分:
- 前向过程:加噪,模型由原始图片逐步变化变成完全的噪声
- 后向过程:去噪,模型由噪声还原成原始图片
为了方便理解,“前向过程”都会表达成“加噪过程”,“后向过程”都会表达成“去噪过程”
1.1 定义与限制
同时,对模型加之以下定义和限制:
- 前向和后向过程均建模成马尔可夫链
马尔科夫链背后的含义是:任何 t + 1 t+1 t+1时刻的状态只与 t t t时刻的状态有关,而与其他时刻无关,这蕴含着形如这的联合概率可展开成 P ( x t + 2 , x t + 1 ∣ x t ) = P ( x t + 2 ∣ x t + 1 ) P ( x t + 1 ∣ x t ) P(x_{t+2},x_{t+1}|x_t) = P(x_{t+2}|x_{t+1}) P(x_{t+1}|x_t) P(xt+2,xt+1∣xt)=P(xt+2∣xt+1)P(xt+1∣xt) 。这里的推导可以通过联合概率公式展开 P ( y , x ) = P ( y ∣ x ) ∗ P ( x ) P(y,x) = P(y|x) * P(x) P(y,x)=P(y∣x)∗P(x) - 加噪过程是无参数的,而去噪过程是有参数的
在Diffusion Model里,加噪过程的encoder被认为是已知的无需参数优化的,是一个以前一时刻的隐变量为中心的高斯模型,记为 q ( x t ∣ x t − 1 ) q(x_t|x_{t-1}) q(xt∣xt−1),而去噪过程的decoder则是需要学习的模型,记为 p θ ( x t − 1 ∣ x t ) p_\theta(x_{t-1}|x_t) pθ(xt−1∣xt) - 最终时刻隐变量 x T ∼ N ( 0 , 1 ) x_T\sim N(0,1) xT∼N(0,1)
- 模型所有时刻的隐变量维度与原始图片相同
这些定义与限制对于理解后续的公式非常重要,本人最开始并没有去真正理解这些,导致了最开始理解DDPM以及相关博客地公式都非常困难。当后来我以这些定义和限制为始,并对原文进行阅读时,公式的理解就顺畅许多。Understanding Diffusion Models: A Unified Perspective非常值得阅读。
1.2 定义与限制的数学体现
p
(
x
0
:
T
)
=
p
(
x
0
,
x
1
,
.
.
.
,
x
T
)
=
p
(
x
T
)
∏
t
=
1
T
p
θ
(
x
t
−
1
∣
x
t
)
(1)
p(x_{0:T}) = p(x_0, x_1, ..., x_T) = p(x_T) \prod_{t=1}^Tp_\theta(x_{t-1}|x_t) \tag{1}
p(x0:T)=p(x0,x1,...,xT)=p(xT)t=1∏Tpθ(xt−1∣xt)(1)
q
(
x
t
∣
x
t
−
1
)
=
N
(
x
t
;
α
t
x
t
−
1
,
(
1
−
α
t
)
I
)
(2)
q(x_t|x_{t-1}) = N(x_t;\sqrt{\alpha_t}x_{t-1}, (1-\alpha_t)\Iota)\tag{2}
q(xt∣xt−1)=N(xt;αtxt−1,(1−αt)I)(2)
p
(
x
T
)
=
N
(
x
T
;
0
,
I
)
(3)
p(x_T) = N(x_T;0, \Iota) \tag{3}
p(xT)=N(xT;0,I)(3)
公式1 是用了马尔可夫链的性质,其中提到的
p
(
x
0
:
T
)
{p(x_{0:T})}
p(x0:T)将会用于后续的求目标函数,公式二则是一个模型选择的问题(为什么模型的均值和方差要采取这种形式?)。
到这里,我们是对diffusion model只是进行了一个定义和限制,以及这种定义之下隐含的数学体现。非常明确的一点是,我们需要对模型的参数部分,也就是后向过程进行参数求解,后续章节则为了参数求解涉及了一套美妙的数学解释。
因为这套数学解释非常复杂,写者在阅读时有两个非常naive的问题:
- 既然加噪过程 q ( x t ∣ x t − 1 ) q(x_t|x_{t-1}) q(xt∣xt−1)时已知的,去噪过程本质就是加噪过程的逆分布,不能从数学公式直接推导吗,非得参数化求解?
答案是No,加噪过程的逆运算 q ( x t − 1 ∣ x t ) = q ( x t ∣ x t − 1 ) q ( x t − 1 ) q ( x t ) q(x_{t-1}|x_t) = \frac{q(x_t|x_{t-1}) q(x_{t-1})}{q(x_t)} q(xt−1∣xt)=q(xt)q(xt∣xt−1)q(xt−1),确实有一部分已知,但公式中的 q ( x t − 1 ) , q ( x t ) q(x_{t-1}), q(x_t) q(xt−1),q(xt)的分布是完全未知且难以建模的,他们也不能先入为主的认为是 N ( 0 , 1 ) N(0, 1) N(0,1),设想 x 1 x_1 x1,这是原始图片加噪一次的结果,其不可能是正态分布,也不可能被简单的建模,其建模的难度等同于 p ( x 0 ) p(x_0) p(x0)- 既然公式推导不了,为啥不考虑一些简单的损失函数,如对输入图片 x 0 ′ x'_0 x0′和groundtruth图片 x 0 x_0 x0做MSE?
我们可以把diffusion model简化来思考这个问题。假设T=1,这个模型本质就是一个variational auto encoder。若只做MSE,不对中间隐变量 x 1 x_1 x1做任何的regularization,则这个模型进一步退化成auto encoder,模型生成的效果必然很差。auto encoder为什么差,可参照这篇文章的分析。问题1的思考也给我带来了一些新的insight。加噪过程的逆分布是我们无法得到或者intractable的,diffusion model的目标其实就是利用参数化的去噪过程去学习和逼近我们设想中的加噪过程的逆分布,即 p θ ( x t − 1 ∣ x t ) p_\theta(x_{t-1}|x_t) pθ(xt−1∣xt)的理想目标就是 q ( x t ∣ x t − 1 ) q(x_t|x_{t-1}) q(xt∣xt−1)的逆分布。
2. Diffusion Model的模型训练
我们已经有了模型的定义,并且对模型已经参数化了,下一步则是需要进行模型训练,这便需要我们提供一个目标函数,也就是所有隐变量的联合密度函数的对数(取对数只是为了方便计算,应该分布往往都是以指数形式存在,如正态分布)。
l
o
g
(
p
(
X
)
)
=
l
o
g
(
p
(
x
0
:
T
)
)
log(p(X)) = log(p(x_{0:T}))
log(p(X))=log(p(x0:T))
Diffusion Model希望最大化概率该密度函数。
在经典的深度学习领域,如分类、检测、分割等,模型的训练往往是需要一个groundtruth的,而目标函数的定义往往衡量的是模型输出与ground truth的差距(如CE、MSE),从而让模型参数朝着减少差距的方向进行参数优化。Diffusion Model的目标函数则无须ground truth,其从统计学的角度建模了随机变量的似然函数,并从最大化似然函数为目标进行求解,3.1小节对最大似然函数进行了补充。
由于 l o g p ( X ) logp(X) logp(X)形式并不能用于求解,需要进行进一步推导,得到易于求解的形式。推导过程我将其分成了几步。
2.1 似然函数转换成ELBO
ELBO貌似是变分推断中常用的一种求解方式,但读者并未完全理解其background以及意义,后续将补充这一相关读书笔记。先留个坑。
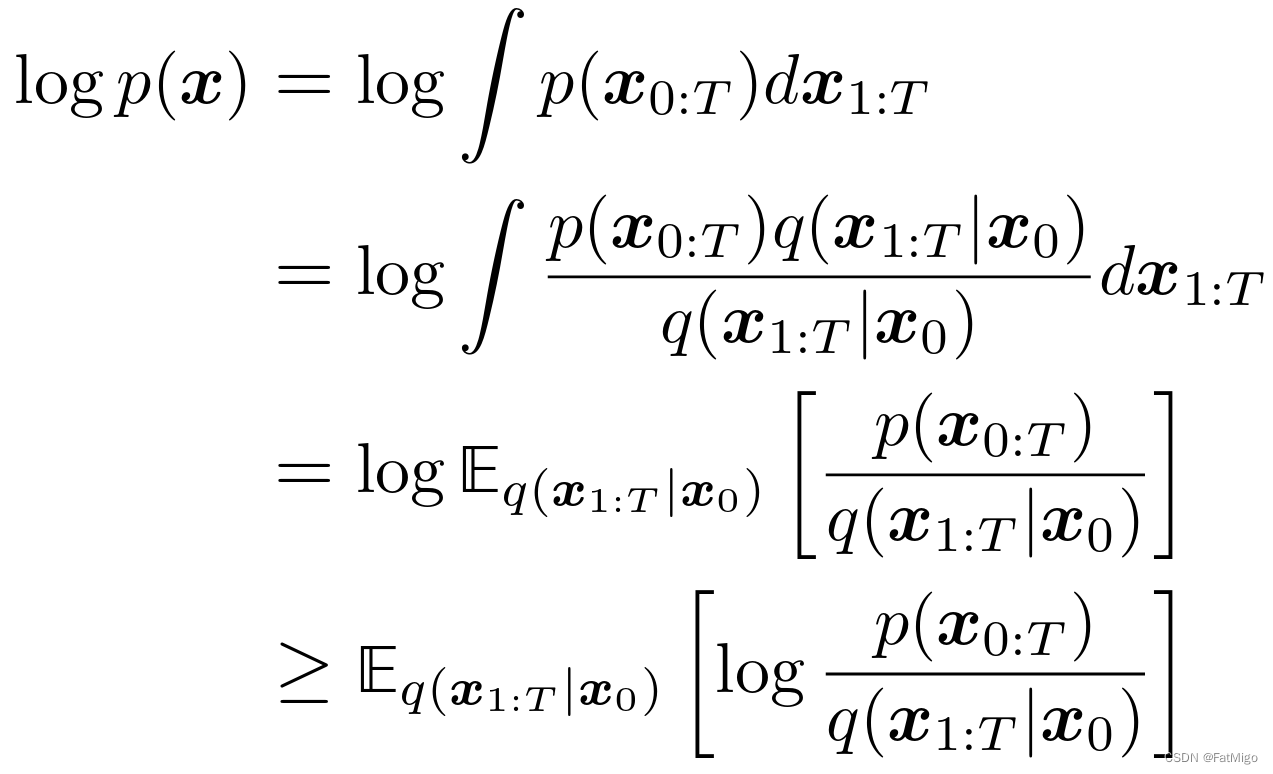
最后一步用到了Jensen不等式。
对数函数与期望的转换是信息论里常用的应用Jensen不等式的例子。另外,一元函数是否为凸函数可以判断其二阶导是否恒>0,因此 l o g ( x ) log(x) log(x)是满足这一性质的。
2.2 拆解ELBO


到这里,优化ELBO需要优化三项:
- E q ( x 1 ∣ x 0 ) [ l o g p θ ( x 0 ∣ x 1 ) ] E_{q(x_1|x_0)}[logp_\theta(x_0|x_1)] Eq(x1∣x0)[logpθ(x0∣x1)]: 最大化这一项表示去噪过程的最后一步需要最大成都还原原始图片
- D K L ( q ( x T ∣ x 0 ) ∣ ∣ p ( x T ) ) D_{KL}(q(x_T|x_0)||p(x_T)) DKL(q(xT∣x0)∣∣p(xT)): 这一项对参数 θ \theta θ而言是恒定值,可以忽略
- ∑ t = 2 T E q ( x t ∣ x 0 ) [ D K L ( q ( x t − 1 ∣ x t , x 0 ) ∣ ∣ p θ ( x t − 1 ∣ x t ) ) ) ] \sum_{t=2}^{T}E_{q(x_t|x_0)}[D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t)))] ∑t=2TEq(xt∣x0)[DKL(q(xt−1∣xt,x0)∣∣pθ(xt−1∣xt)))]: 这一项是表示去噪过程的每一步的分布 p θ ( x t − 1 ∣ x t ) ) p_\theta(x_{t-1}|x_t)) pθ(xt−1∣xt))需要最大化地拟合分布 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0)
到这里,一系列推导给出了一个比较直观地理解:我们原本希望 p θ ( x t − 1 ∣ x t ) ) p_\theta(x_{t-1}|x_t)) pθ(xt−1∣xt))希望逼近 q ( x t ∣ x t − 1 ) q(x_{t}|x_{t-1}) q(xt∣xt−1)的逆分布 q ( x t − 1 ∣ x t ) q(x_{t-1}|x_t) q(xt−1∣xt),而逆分布是intractable的(如1.2小节提到)。通过ELBO以及一些列推导,我们转换成了 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0),而该分布是有可能tractable的,也就是其形式是可知的。一旦知道其形式,就能得到参数优化的求解公式
2.3 求解关键: q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0)的显示表达
首先,应用贝叶斯公式:
q
(
x
t
−
1
∣
x
t
,
x
0
)
=
q
(
x
t
∣
x
t
−
1
,
x
0
)
∗
q
(
x
t
−
1
∣
,
x
0
)
q
(
x
t
∣
x
0
)
=
q
(
x
t
∣
x
t
−
1
)
∗
q
(
x
t
−
1
∣
,
x
0
)
q
(
x
t
∣
x
0
)
q(x_{t-1}|x_t,x_0) = \frac{q(x_{t}|x_{t-1},x_0) * q(x_{t-1}|,x_0)}{q(x_{t}|x_0)}= \frac{q(x_{t}|x_{t-1}) * q(x_{t-1}|,x_0)}{q(x_{t}|x_0)}
q(xt−1∣xt,x0)=q(xt∣x0)q(xt∣xt−1,x0)∗q(xt−1∣,x0)=q(xt∣x0)q(xt∣xt−1)∗q(xt−1∣,x0)
而 q ( x t ∣ x t − 1 ) q(x_t|x_{t-1}) q(xt∣xt−1)的分布密度函数是已知的,上述问题的关键就转换成了求 q ( x t ∣ x 0 ) q(x_t|x_0) q(xt∣x0)的显示表达。这里需要用到一个重参技巧(reparameterization trick:
若
x
t
∼
q
(
x
t
∣
x
t
−
1
)
=
N
(
x
t
;
α
t
x
t
−
1
,
(
1
−
α
t
)
I
)
x_t \sim q(x_t|x_{t-1}) = N(x_t;\sqrt{\alpha_t}x_{t-1}, (1-\alpha_t)\Iota)
xt∼q(xt∣xt−1)=N(xt;αtxt−1,(1−αt)I),转换为
x
t
=
α
t
x
t
−
1
+
1
−
α
t
ϵ
,
ϵ
∼
N
(
0
,
I
)
x_t = \sqrt{\alpha_t}x_{t-1} + \sqrt{1-\alpha_t}\epsilon, \epsilon \sim N(0, \Iota)
xt=αtxt−1+1−αtϵ,ϵ∼N(0,I)
以此类推,就比较容易得到下列事实:
x
t
∼
q
(
x
t
∣
x
0
)
=
N
(
α
ˉ
t
x
0
,
(
1
−
α
ˉ
t
)
I
)
x_t \sim q(x_t|x_0) = N(\sqrt{\bar{\alpha}_t}x_0,(1-\bar\alpha_t)\Iota)
xt∼q(xt∣x0)=N(αˉtx0,(1−αˉt)I)
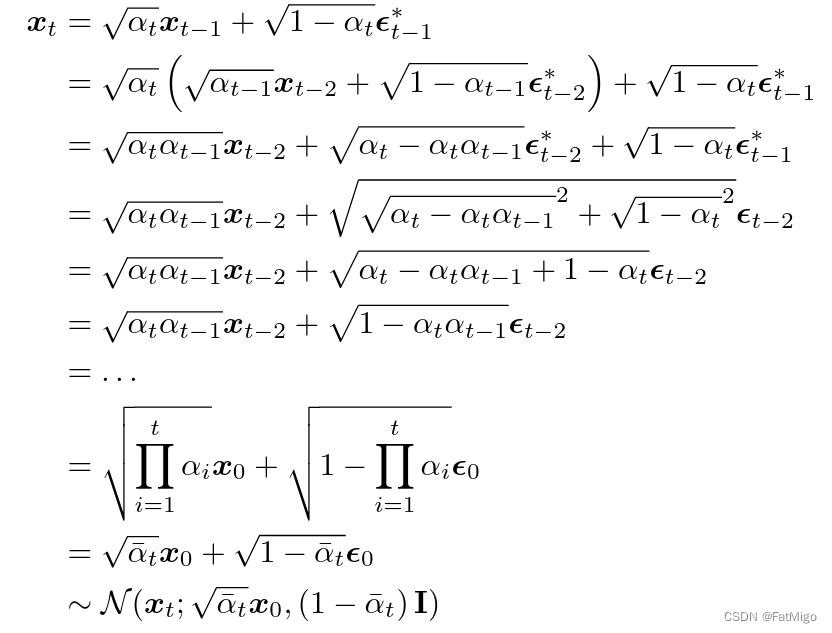
因此,
q
(
x
t
−
1
∣
x
t
,
x
0
)
q(x_{t-1}|x_t,x_0)
q(xt−1∣xt,x0)的形式也比较容易得到,这里也不展开了。
综上,Diffusion Model的最大似然函数的优化目标可以显示地表达出来,结合我们训练数据即可得到我们的最优参数。
一个非常有趣的感悟是:也许一开始有人会想到 q ( x t − 1 ∣ x t ) q(x_{t-1}|x_t) q(xt−1∣xt)是intractable,而 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0)可以借助贝叶斯公式变成tractable。直接用 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0)近似 q ( x t − 1 ∣ x t ) q(x_{t-1}|x_t) q(xt−1∣xt)求解,即可免去了上述一系列的ELBO及其后续的推导。这种近似虽然直觉上很好理解并觉得合理,但却缺乏数学支持而显得非常无力并难以信服。数学推导尽管痛苦,但却从理论上保证了可行性,这回答了一个非常本质的问题:以这个目标函数训练为什么能work。人们常说,人是无法赚到认知以外的钱的。而数学原理的保障给我们提供了认知,让我们能赚到这里面的钱:那就是确保模型训练的有效性,这莫不是是数学之美的一个体现。
3. 附录
3.1 最大化似然函数
这里举个最大化似然函数求解的例子。假设已知随机变量
x
∼
N
(
θ
,
σ
2
)
x \sim N(\theta, \sigma^2)
x∼N(θ,σ2),现在有俩抽样样本,值分别1,2。则似然函数刻画的是出现这俩样本的概率
P
(
x
1
=
1
,
x
2
=
2
)
=
P
(
x
1
=
1
)
∗
P
(
x
2
=
2
)
=
1
2
π
σ
e
x
p
(
−
(
1
−
μ
)
2
2
σ
2
)
∗
1
2
π
σ
e
x
p
(
−
(
2
−
μ
)
2
2
σ
2
)
\begin{aligned} P(x_1 = 1, x_2 = 2) & = P(x_1 = 1) * P(x_2 = 2) \\ & = \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(1-\mu)^2}{2\sigma^2}) * \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(2-\mu)^2}{2\sigma^2}) \\ \end{aligned}
P(x1=1,x2=2)=P(x1=1)∗P(x2=2)=2πσ1exp(−2σ2(1−μ)2)∗2πσ1exp(−2σ2(2−μ)2)
取对数后则为
l
o
g
(
P
(
x
1
=
1
,
x
2
=
2
)
)
=
−
l
o
g
(
2
π
)
−
2
l
o
g
(
σ
)
−
1
2
σ
2
(
(
1
−
μ
)
2
+
(
2
−
μ
)
2
)
\begin{aligned} log(P(x_1 = 1, x_2 = 2)) & = -log(2\pi) - 2log(\sigma) - \frac{1}{2\sigma^2}((1-\mu)^2 + (2-\mu)^2) \end{aligned}
log(P(x1=1,x2=2))=−log(2π)−2log(σ)−2σ21((1−μ)2+(2−μ)2)
然后通过求导求最大值的方式得到 μ = μ ∗ , σ = σ ∗ \mu=\mu^*,\sigma = \sigma* μ=μ∗,σ=σ∗