Python——线性回归、梯度下降、正则化（原理）

news2024/11/16 0:02:08

1 线性回归-最小二乘法(LSM)

2 梯度下降

3 数据归一化/标准化

4 过拟合和欠拟合

4.1 过拟合的处理

4.2 欠拟合的处理

5 正则化

一种通过属性的线性组合来进行预测的线性模型，其目的是找到一条直线或者一个平面或者更高维的超平面，使得预测值与真实值之间的误差最小化。

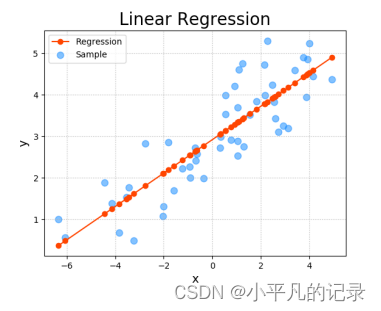
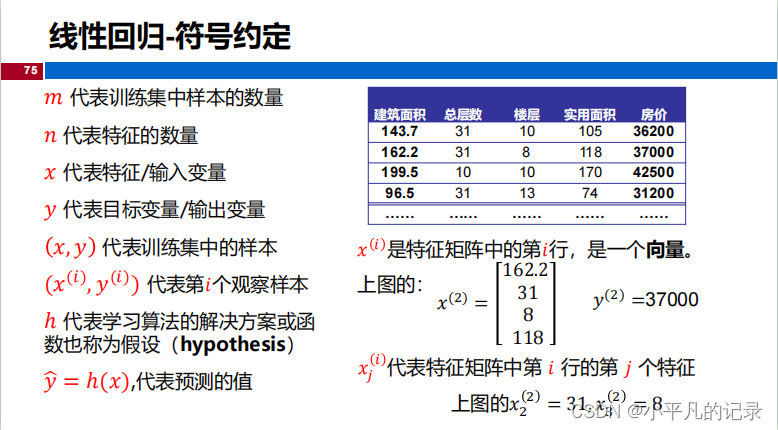
损失函数(Loss Function)

度量单样本预测的错误程度，损失函数值越小，模型就越好。常用的损失函数包括：0-1损失函数、平方损失函数、绝对损失函数、对数损失函数等。

代价函数(Cost Function)

度量全部样本集的平均误差。常用的代价函数包括均方误差、均方根误差、平均绝对误差等。

目标函数(Object Function)

代价函数和正则化函数，最终要优化的函数。

备注：损失函数的系数1/2是为了便于计算，使对平方项求导后的常数系数为1，这样在形式上稍微简单一些。有些教科书把系数设为1/2，有些设置为1，这些都不影响结果。

1 线性回归-最小二乘法(LSM)

2 梯度下降

批量梯度下降（Batch Gradient Descent,BGD）

梯度下降的每一步中，都用到了所有的训练样本

随机梯度下降（Stochastic Gradient Descent,SGD）

梯度下降的每一步中，用到一个样本，在每一次计算之后便更新参数，而不需要首先将所有的训练集求和

小批量梯度下降（Mini-Batch Gradient Descent,MBGD）

梯度下降的每一步中，用到了一定批量的训练样本

梯度下降与最小二乘法比较

梯度下降：需要选择学习率𝛼，需要多次迭代，当特征数量𝑛大时也能较好适用，适用于各种类型的模型。

最小二乘法 ：不需要选择学习率 𝛼 ，一次计算得出，需要计算 $(X^TX)^{-1}$ ，如果特征数量𝑛 较大则运算代价大，因为矩阵逆的计算时间复杂度为𝑂(𝑛^ 3 ) ，通常来说当 𝑛 小于10000 时还是可以接受的，只适用于线性模型，不适合逻辑回归模型等其他模型。

3 数据归一化/标准化

需要做数据归一化/标准化

线性模型，如基于距离度量的模型包括KNN(K近邻)、K-means聚类、感知机和SVM。另外，线性回归类的几个模型一般情况下也是需要做数据归一化/标准化处理的。

不需要做数据归一化/标准化

决策树、基于决策树的Boosting和Bagging等集成学习模型对于特征取值大小并不敏感，如随机森林、XGBoost、LightGBM等树模型，以及朴素贝叶斯，以上这些模型一般不需要做数据归一化/标准化处理。

4 过拟合和欠拟合

4.1 过拟合的处理

1.获得更多的训练数据

使用更多的训练数据是解决过拟合问题最有效的手段，因为更多的样本能够让模型学习到更多更有效的特征，减小噪声的影响。

2.降维

即丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征，或者使用一些模型选择的算法来帮忙（例如PCA ）。

3.正则化

正则化 (regularization) 的技术，保留所有的特征，但是减少参数的大小（ magnitude ），它可以改善或者减少过拟合问题。

4.集成学习方法

集成学习是把多个模型集成在一起，来降低单一模型的过拟合风险。

4.2 欠拟合的处理

1.添加新特征

当特征不足或者现有特征与样本标签的相关性不强时，模型容易出现欠拟合。通过挖掘组合特征等新的特征，往往能够取得更好的效果。

2.增加模型复杂度

简单模型的学习能力较差，通过增加模型的复杂度可以使模型拥有更强的拟合能力。例如，在线性模型中添加高次项，在神经网络模型中增加网络层数或神经元

个数等。

3.减小正则化系数

正则化是用来防止过拟合的，但当模型出现欠拟合现象时，则需要有针对性地减小正则化系数。

5 正则化

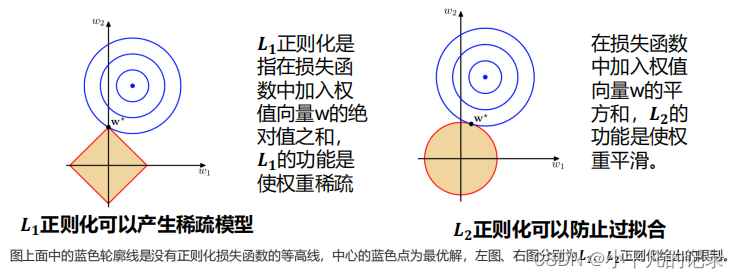
可以看到在正则化的限制之下，𝑳𝟐正则化给出的最优解w*是使解更加靠近原点，也就是说𝑳𝟐正则化能降低参数范数的总和。

𝑳 𝟏 正则化给出的最优解 w* 是使解更加靠近某些轴 , 而其它的轴则为 0，所以 𝑳 𝟏 正则化能使得到的参数稀疏化。

6 简单代码

from sklearn.metrics import mean_squared_error  #评价指标

#从sklearn算法库中导入线性回归模型算法
from sklearn.linear_model import c
clf = LinearRegression()#线性回归模型
clf.fit(train_data, train_target)#拟合
test_pred = clf.predict(test_data)#预测
score = mean_squared_error(test_target, clf.predict(test_data))#均方误差
print("LinearRegression:   ", score)


LinearRegression:    0.2642337917628173