​《Protein Actions Principles and Modeling》-《蛋白质作用原理和建模》

本人能力有限，如果错误欢迎批评指正。

第六章：The principles of protein folding kinetics

（蛋白质折叠动力学的原理）

整个二级结构通常作为一个单元进行折叠

蛋白质倾向于以基序或二级结构的单位折叠，而不是以单个的氨基酸的形式进行折叠。结构折叠单元被称为折叠单元或部分展开的形式(foldons or partially unfolded forms)。用氢交换法(hydrogen exchange)（HX）观察到折叠子。HX可以测量平衡变化以及折叠动力学的性质。在平衡HX中，你有一系列增加变性剂的蛋白质溶液。每个氨基酸都有一个酰胺质子。在实验之前，用氘原子取代那些酰胺质子。在溶液中，蛋白质上的氘原子会与周围溶剂水中的氢原子交换，其平衡常数取决于这些酰胺基团暴露在水中的程度。研究发现，在一系列不断增加的变性剂中，整个二级结构往往同时被质子化。在动力学HX中，你瞬时地改变条件，以捕获在折叠的特定时间间隔内蛋白质的质子化状态。这两个实验都表明，二级结构可以快速折叠。图6 11显示了细胞色素c中单个结构元素的稳定性序列。有些蛋白质折叠得如此之快，以至于它们似乎基本上没有自由能的势垒。它们被称为超快折叠者(ultrafast folders)，它可以在几十微秒的时间尺度上折叠。

图6.11细胞色素c以折叠体为单位进行折叠。折叠单元是一对两个末端螺旋，形成一个三级接触（蓝色）；一个中心的60's螺旋和环（绿色）；连接到绿色区域的双链β-sheet（黄色）；和两个环（红色和白色）。

超快折叠者揭示了蛋白质折叠的速度限制

那么我们如何才能确定一个过程是否是无能垒的呢？首先，一个没有能垒的过程是快速的。其次，动力学势垒的缺失意味着折叠过程没有两个可区分的状态，因此也就不存在双态（单指数）动力学。无能垒过程可以有复杂的动力学。第三，在一个具有能垒折叠的chevron图中，在低变性剂下的折叠速率系数与变性剂浓度无关。将变性剂浓度降低到某一点也不会加速折叠的过程，因为这个时候的折叠速率已经是最大的(图6.9)。第四，无能垒的过程不符合Arrhenius动力学。方程6.19描述了包含一个势垒的双态折叠是如何遵循Arrhenius动力学的。当折叠过程有一个能垒的时候，更高的温度会导致更快的速率。但当没有能垒时，折叠已经以最大可能的速度发生了，所以提高温度不会进一步加速它。图6.12显示了一种蛋白质，这种蛋白不会随着温度的增加而加快折叠的速度。在超快折叠中，kf(T)随温度近似恒定。然而，有趣的是，超快折叠蛋白的展开通常遵循Arrhenius动力学。

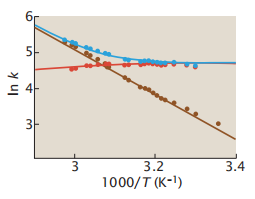
图6.12 无能垒折叠的证据：折叠速率系数（红色）几乎与温度无关（对于嵌入的同源结构域蛋白。相反，展开速率系数（棕色）遵循Arrhenius动力学。观察到的速率系数（蓝色）是折叠速率和展开速率的总和。

在本章的其余部分中，我们将目光从实验和宏观模型转移到在蛋白质结构中如何进行折叠过程编码的微观建模。宏观理论的目的是捕获关于动力学宏观状态的实验数据，如N，D，和I1，I2，……。宏观模型并不是为了解释折叠的物理基础，或者为什么一种蛋白质的折叠不同于另一种，或者不同的溶剂或温度条件如何加速或减缓折叠，或者预测折叠速率。

-蛋白质是如何折叠得这么快的？它们可以折叠在漏斗状的能源景观上

让我们回到 Levinthal的问题上来：蛋白质怎么能折叠得这么快？小蛋白质是如何独立做到这一点的，独立于它们的氨基酸序列，独立于开始变性条件，也不考虑链从什么变性构象开始？这些问题可以通过识别蛋白质折叠能量景观的形状来回答。能量景观是一个自变量x1,x2,x3…的数学函数G（x1,x2,x3,…xL）。蛋白质的自变量xi是链构象自由度，对于n个原子的系统，共L = 3n−6，不包括6个外部自由度（3个刚体平移自由度和3个刚体旋转自由度）。这些变量可以用许多几何特征来描述，例如键角、键长、分子间距离以及水分子的位置和取向。对于蛋白质折叠，函数G是自由能。G是一个高维的面，因为它依赖于蛋白质的各种自由度。这个函数G的性质是什么？作为变量xi的函数，G的曲面的形状是什么？

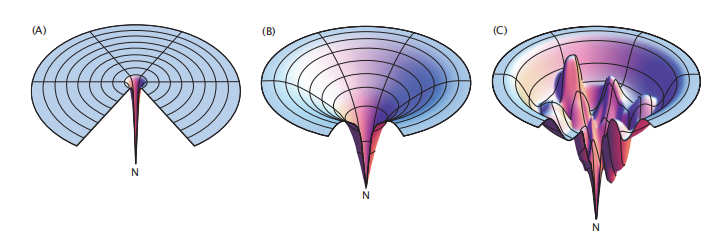
图6.13 能量景观有助于可视化蛋白质折叠过程。(A)的“高尔夫球场”能源景观到处都是平坦的，除了最小的折叠状态。就像在 Levinthal悖论中一样，在这样的景观上折叠需要很长一段时间，因为只有通过对整个大构象空间的随机扩散搜索，才能找到原生结构。(B)蛋白质折叠更恰当地用漏斗能量景观来描述，其中每一个随机的构象步骤导致能量下降（y轴）也会导致进一步构象搜索的减少，说明蛋白质折叠可以如此之快。(C)崎岖的能量景观表明了典型蛋白质在折叠时遇到的动力学凹陷（局部最小值）。

让我们来考虑一下一些可能性。一个蛋白质的折叠能量景观可能具有在一个高维空间中的高尔夫球场的形状（图6.13A）。也就是说，G可能在任何地方都是完全平坦的，除了一个高度局部的凹陷-这代表自然结构，其中自由能在自然条件下必须低于所有其他状态（因为自然状态是稳定的）。高尔夫球场景观意味着链的所有构象都具有相同的内部自由能，除了自然状态，它具有较低的内部自由能。

然而，在20世纪80年代发展起来的统计力学理论表明，可折叠的自由能景观的形状并不像高尔夫球场。它们的形状像漏斗-可折叠的能源景观顶部大而开放，底部小而封闭。漏斗的形状来自于蛋白质分子状态的统计力学密度。能量景观中有许多开链构象，它们共同具有高熵和很少有紧凑的低自由能的原生态。自由能最小化的热力学原理意味着你可以把平衡的倾向比喻为一个滚下山的球。如果在高尔夫球场上随机滚动一个球，那么需要很长时间才能在一个隐喻性的高维景观上找到一个洞，这意味着折叠会非常慢。但是如果在一个漏斗上随机滚动一个球，即使是一个非常高维的球，球也会滚到下坡找到底部-无论它从漏斗的哪里开始。这既表明了蛋白质的折叠是为何是如此之快，也表明了如何从大量不同的变性微观状态中获得天然结构。

可以从折叠漏斗中学到什么？

首先，漏斗解释了溶液溶液中的蛋白质如何从不同的变性微观状态快速地达到相同的天然结构。大多数蛋白质，不管氨基酸序列如何，都会在漏斗状的景观上折叠，因为它们从许多展开的状态折叠到一个或几个天然结构。漏斗也解释了动力学的异质性，即不同的单个链构象通过不同的微观折叠轨迹到达自然结构，这过程的速率可能也不同（图6.14）。这种折叠的异质性是在微观状态水平，而不是宏观状态水平。要在这个微观水平上了解动态异质性，需要观察的不仅仅是平均折叠速率系数kf-还需要测量有多少折叠通过不同可能的微观路径。单分子实验使测量成为可能-它可以看到单个分子的个体轨迹。此外，简单的模型对Levinthal悖论-蛋白质如何折叠得如此之快，给出了一个定量的答案-以毫秒计，而不是数百万年。

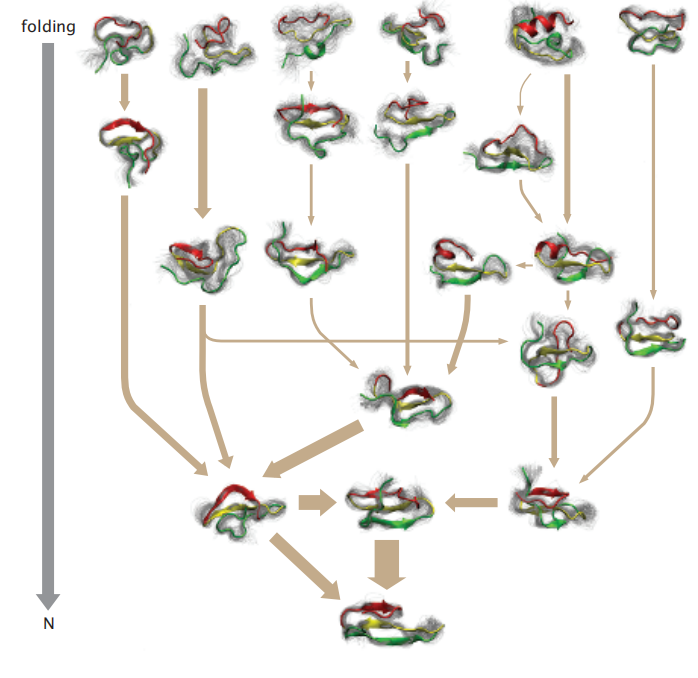
图6.14 在显微镜下，链通过多种路径折叠。这张图显示了Pin WW域折叠的分子动力学模拟。箭头的厚度表示在模拟中所看到的不同构象跃迁的相对频率。

ZSB模型显示了蛋白质折叠速度甚至可以产生相当浅的折叠漏斗。当单个的类天然相互作用比非天然相互作用仅更有利1-2千卡mol−1时，就能达到典型的蛋白质折叠速度。另一类模型被称为Go模型，以它们的起源者N Go命名，它对折叠漏斗和单个蛋白质的折叠路线提供了有用的见解。在Go模型只为天然接触分配积极有利的相互作用。这样，就可以把真正的能源景观变成一个光滑的漏斗，去探索到折叠状态的最有效的路径。另一个主要的模型是自旋玻璃( spin-glass)模型，它给出了一个简单的近似方法来描述折叠能量景观的碰撞特征.

此外，折叠漏斗的卡通图还可以传达出有用的信息。例如，图6.13A显示了高尔夫球场景观，说明了无限慢随机搜索的早期预期；图6.13B显示了一个平滑的漏斗，表明快速折叠；图6.13C显示了一个凹凸不平的漏斗，表明了可以降低折叠速度的小动力学凹陷。

这里也有漏状景观折叠的实验证据。例如，D Barrick等人研究了重复蛋白质(repeat proteins)，即具有多个可折叠肽的分子。每个重复单元都可以单独折叠，但它们的折叠速率和平衡也依赖于单元之间的合作相互作用。这些蛋白质的折叠是同时发生的，因为有许多等效的重复模块亚基（图6.15）。

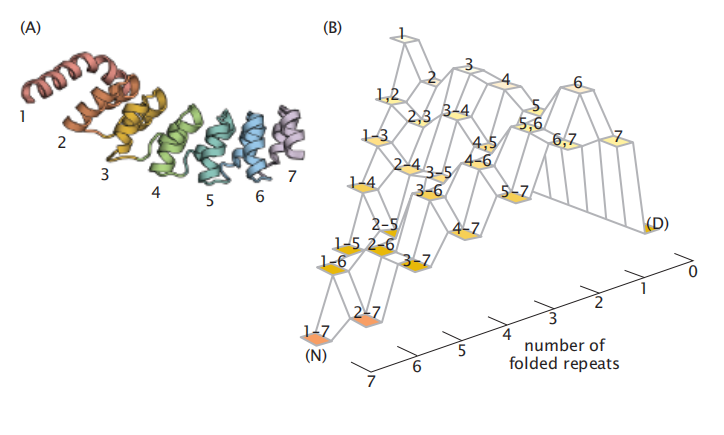
图6.15 一个重复结构域蛋白适合于详细的测量，显示了一个漏斗形的折叠景观。(A)Notch锚定蛋白有7个重复单元。折叠可以在单个领域中进行测量。(B)折叠态的能量景观显示为折叠重复的数量及其位置的函数。

-不同的蛋白质可以以非常不同的速度折叠

白质的折叠速度不仅取决于突变、温度和变性剂。蛋白质的折叠速度也取决于蛋白质的天然结构。蛋白质的序列和结构是如何编码其折叠速率和路线的？哪些构象被探索，哪些没有？有一个普遍的折叠机制吗？也就是说，是否有一个适用于不同类型的蛋白质的一系列结构事件的描述？在这里，我们介绍一些将蛋白质结构与折叠速度相关联的观察结果。

了解一种蛋白质的天然结构可以有助于预测它的折叠速度。图6.16显示了折叠速度如何依赖于原生结构的特征。折叠速度随数量级而变化。图6.16A显示，折叠速率与天然结构的绝对接触顺序（ACO,Absolute contact order）相关，这是蛋白质天然接触的“局部性”的度量。在其天然结构中有更多的本地接触和较少的非本地接触的蛋白质往往能更快地进行折叠。α-螺旋蛋白往往比β蛋白折叠得更快。图6.16B中类似的相关性表明，蛋白质的二级结构越多，蛋白质的平均折叠速度就越慢。为什么添加二级结构会减慢折叠过程？

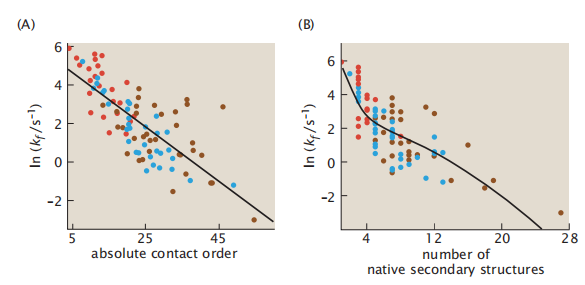
图6.16 结构特征决定折叠速率。(A)折叠速率与蛋白质天然结构的绝对接触顺序（ACO）相关。ACO测量蛋白质接触的平均“非局部性”。蛋白质的螺旋折叠更快，而β折叠的蛋白质折叠更慢。ACO =（1/CN）∑ΔCij，其中CN为天然接触总数，Cij≡|j−i|为残基i和j之间的接触顺序，它们之间沿序列的分离。(B)对于具有更多二级结构的蛋白质的折叠速率较慢。红色表示α-螺旋蛋白，蓝色的β蛋白和棕色的α-β蛋白。

折叠动力学的基本单位是折叠子(foldon)。折叠似乎是由单个二级结构上发生的。尽管天然蛋白质的单个二级结构本身并不稳定，但它们比其他结构更稳定，并且可以通过组装成三级结构来进一步稳定。

主要的折叠路径以局部第一、全局为后的顺序形成结构。在从展开到折叠条件下，聚合物分子只能在最早的时间尺度上在链的小部分内进行局部构象采样。例如，一个螺旋或一个β链对的旋转。形成非局部接触需要更大的搜索时间和更长的时间。在中间长度的时间尺度上，一条局部的链可以生长或压缩成更大的局部结构，如全螺旋或β链对。在最慢的时间尺度上，二级结构片段有时间聚集在一起并组装成蛋白质的三级结构。局部优先、全局为后可以快速找到蛋白质的天然结构。例如，实验表明，插入长度增加的聚甘氨酸环，增加了构象搜索，也会减缓折叠的速度。

图6.17 显示了一种能够接受的折叠机制，称为折叠子组装模型(Foldon Assembly Model)。首先，一个折叠体在链的某个地方形成。它形成的非常迅速但数量较少。然后，第二个折叠子通过聚集在第一个折叠体上而形成。这种双折叠组合的数量甚至比它的前身单折叠组合还要低。这一过程还在继续，额外的二级结构聚集在不断增长的框架上，结构数量不断减少（因为每个增加的螺旋都是自由能上坡的一步）。最后一步是形成自然结构，这时候具有高分布（低自由能）-因为当蛋白质的自然状态具有额外的包装和稳定的相互作用。就在到达天然结构之前，蛋白质通过其折叠过渡状态。因此能量景观呈火山形状：首先是上坡，最后是下坡（图6.18)。

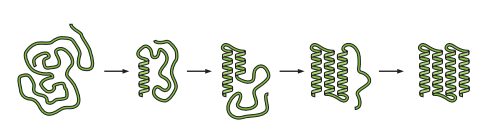
图6.17 折叠子组装模型。在自然条件下，二级结构会开关开关地闪烁，但大多是关闭。但有时当它打开时，另一个二级结构也会闪烁，与第一个相邻并被它稳定下来。二级结构的增加会导致折叠的后期阶段比早期阶段“更不稳定”。直到在最后一步形成一个完全稳定的自然结构（即稳定的折叠结构），整个结构才算稳定下来。

折叠子组装模型是一种通用的折叠机制：(i)二级结构不是单独稳定的。（ii）三级结构的相互作用有助于稳定结构。（iii）双态蛋白质在D和N之间有一个自由能势垒（因此，是单指数动力学）。（iv）最慢的速度的弛豫时间应该与其起始变性构象无关。蛋白质的起始状态只影响快速过程。缓慢的过程与链是从完全变性开始还是从其他一些具有一些剩余初始结构的构象开始无关。(v)随着二级结构数量的增加，折叠速度变得更慢（见图6.16）。该模型给出了一个通用的机制，适用于双态蛋白质，在许多不同的折叠上，并从已知的量估计折叠速率，如螺旋-线圈和三级倾向。

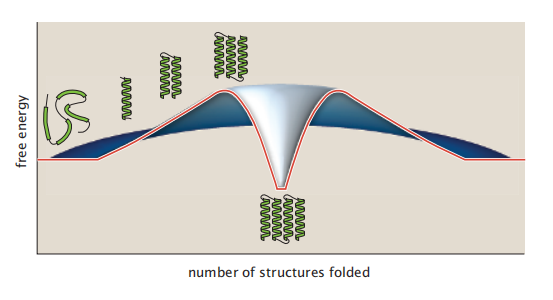
图6.18 折叠子组装模型的火山形折叠能量景观形状。折叠是具有顺序的：折叠1形式，然后折叠2添加到它，然后折叠3，等等。这些步骤都是自由能的上坡，因为每个单独的二级结构都是能量不利的。只有进入完全原生状态的最后一步是自由能的下坡路。

-总结

对蛋白质折叠和展开速率的测量可以深入了解折叠过程的顺序，以及蛋白质如何快速地折叠，尽管它们的序列和天然结构如此复杂和多样性。通过Φ-值分析、氢交换和其他实验所发现的那样，温度、变性剂的浓度和蛋白质的大小也会影响蛋白质的折叠速率。较小的蛋白质通常通过单指数动力学折叠，而较大的蛋白质通常通过多指数动力学折叠（涉及动力学中间体）。主方程式提供了一种捕捉这种现象学的方法。微观模型根据漏斗形的能量景观来解释蛋白质折叠的速度。ZSB模型显示了一个相对较小的能量偏置（漏斗）如何足以解释蛋白质折叠的高速。在折叠子组装模型中，折叠子迅速形成，然后组装成一个越来越天然的双态蛋白质结构。这些简单的模型让我们深入了解蛋白质如何相对快速地直接折叠成其天然结构。

第六章完

-------------------------------------------

欢迎点赞收藏转发！

下次见！