( “树” 之 BST) 653. 两数之和 IV - 输入二叉搜索树 —

( “树” 之 BST) 653. 两数之和 IV - 输入二叉搜索树 ——【Leetcode每日一题】

news2024/10/5 23:25:00

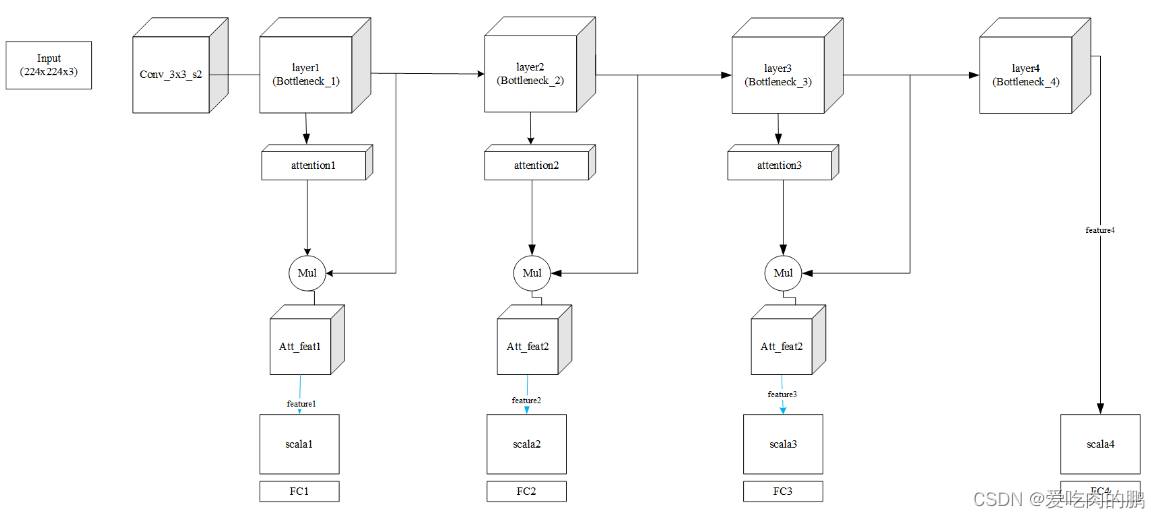
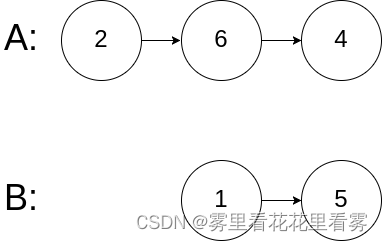
二叉查找树（BST）：根节点大于等于左子树所有节点，小于等于右子树所有节点。
二叉查找树中序遍历有序。

653. 两数之和 IV - 输入二叉搜索树

难度：简单

给定一个二叉搜索树 root 和一个目标结果 k，如果二叉搜索树中存在两个元素且它们的和等于给定的目标结果，则返回 true。

示例 1：

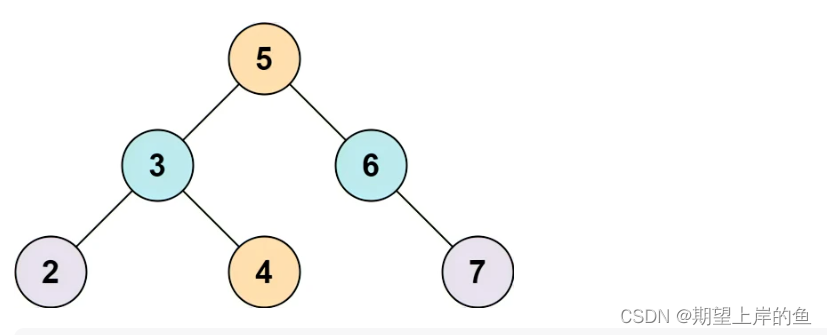
在这里插入图片描述

输入: root = [5,3,6,2,4,null,7], k = 9
输出: true

示例 2：

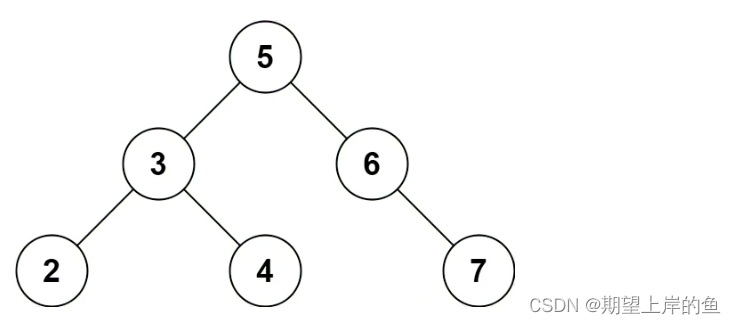
在这里插入图片描述

输入: root = [5,3,6,2,4,null,7], k = 28
输出: false

提示:

二叉树的节点个数的范围是 $1, 10^4].$
$10^4 <= Node.val <= 10^4$
题目数据保证，输入的 root 是一棵有效的二叉搜索树
$10^5 <= k <= 10^5$

思路：

法一：BST中序遍历 + 双指针

使用中序遍历得到有序数组之后，再利用双指针对数组进行查找。

双指针具体思路请看：两数之和 II - 输入有序数组

应该注意到，这一题不能用分别在左右子树两部分来处理这种思想，因为两个待求的节点可能分别在左右子树中。

法二：哈希表

在递归搜索过程中记录下相应的节点值（使用 Set 集合）

如果在遍历某个节点 x 时发现集合中存在 k−x.val，说明存在两个节点之和等于 k，返回 true，
若搜索完整棵树都没有则返回 false。

代码（Java、C++)

法一：BST中序遍历 + 双指针
Java

class Solution {
    public boolean findTarget(TreeNode root, int k) {
        List<Integer> nums = new ArrayList<>();
        inOrder(root, nums);//先得到有序数组
        int i = 0, j = nums.size() - 1;
        while (i < j) {
            int sum = nums.get(i) + nums.get(j);
            if (sum == k) return true;
            if (sum < k) i++;
            else j--;
        }
        return false;
    }
    private void inOrder(TreeNode root, List<Integer> nums) {
        if (root == null) return;
        inOrder(root.left, nums);
        nums.add(root.val);
        inOrder(root.right, nums);
    }
}

C++

class Solution {
public:
    bool findTarget(TreeNode* root, int k) {
        vector<int> nums;
        inOrder(root, nums);//先得到有序数组
        int i = 0, j = nums.size() - 1;
        while (i < j) {
            int sum = nums[i] + nums[j];
            if (sum == k) return true;
            if (sum < k) i++;
            else j--;
        }
        return false;
    }
    void inOrder(TreeNode* root, vector<int> &nums) {
        if (root == nullptr) return;
        inOrder(root->left, nums);
        nums.push_back(root->val);
        inOrder(root->right, nums);
    }
};

法二：哈希表
Java

class Solution {
    Set<Integer> set = new HashSet<>();
    public boolean findTarget(TreeNode root, int k) {
        if(root == null) return false;
        if(set.contains(k - root.val)) return true;
        set.add(root.val);
        return findTarget(root.left, k) || findTarget(root.right, k);
    }
}

C++

class Solution {
public:
    set<int> st;
    bool findTarget(TreeNode* root, int k) {
       if(root == nullptr) return false;
       if(st.find(k - root->val) != st.end()) return true;
       st.insert(root->val);
       return findTarget(root->left, k) || findTarget(root->right, k);
    }
};