union-find API:
class UF {
public:
/* 将 p 和 q 连接 */
void union(int p, int q);
/* 判断 p 和 q 是否连通 */
bool connected(int p, int q);
/* 返回图中有多少个连通分量 */
int count();
};
连通性概念
触点:每个单独的不与任何点相连的点叫做触点
连通分量:简称分量,不存在连接关系的触点和连通在一起的触点的集合都是连通分量
等价关系:处于同一连通分量的触点为等价关系,即他们是连通的
0~9 任意两个不同的点都不连通,调用
connected都会返回 false,连通分量为 10 个。如果现在调用
union(0, 1),那么 0 和 1 被连通,连通分量降为 9 个。再调用
union(1, 2),这时 0,1,2 都被连通,调用connected(0, 2)也会返回 true,连通分量变为 8 个
好啦现在大概知道什么是连通性和连通分量了吧
如果某两个节点被连通,则让其中的(任意)一个节点的根节点接到另一个节点的根节点上
这里connect的实现思路就是把连通的父类之间相连接
class UF {
private:
int count = 0; // 记录连通分量
int* parent; // 节点x的父节点是parent[x]
public:
UF(int n) {
this->count = n;
parent = new int[n];
for(int i = 0; i < n; i++) {
parent[i] = i;
}
}
void Union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if(rootP == rootQ) return;
parent[rootP] = rootQ;
count--;
}
bool connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
int find(int x) {
// 根节点的parent[x] == x,层层向上找就好啦
while(parent[x] != x) {
x = parent[x];
}
return x;
}
(只是一种connect方式,充分不必要,不要老想着问为什么不直接点对点接,有些东西就是因为直接做做不了,才退而求其次间接去做)
大体思路就是这样,但是这么做太直接,无法避免不平衡树(退化成链表)的出现
下面就是优化算法的时间复杂度 => 就是在想法子来降低树的高度
1. 平衡性优化
主要就是把小一些的树接到大一些的树下面,引入“重量”来实现这一目的
通过比较树的重量,就可以保证树的生长相对平衡,树的高度大致在 logN 这个数量级
class UF {
private:
int count = 0; // 记录连通分量
int* parent; // 节点x的父节点是parent[x]
int* size;
public:
UF(int n) {
this->count = n;
parent = new int[n];
size = new int [n];
for(int i = 0; i < n; i++) {
parent[i] = i;
size[i] = 1;
}
}
void Union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if(rootP == rootQ) return;
// 小树接到大树下面
if(size[rootP] > size[rootQ]) {
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
}else {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}
count--;
}
bool connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
int find(int x) {
// 根节点的parent[x] == x,层层向上找就好啦
while(parent[x] != x) {
x = parent[x];
}
return x;
}
int getCount() { return count; }
};2. 路径压缩
我们关注的其实就只有根节点 => 树压的越低越好
int find(int x) {
// 根节点的parent[x] == x,层层向上找就好啦
if(parent[x] != x) parent[x] = find(parent[x]);
return parent[x];
}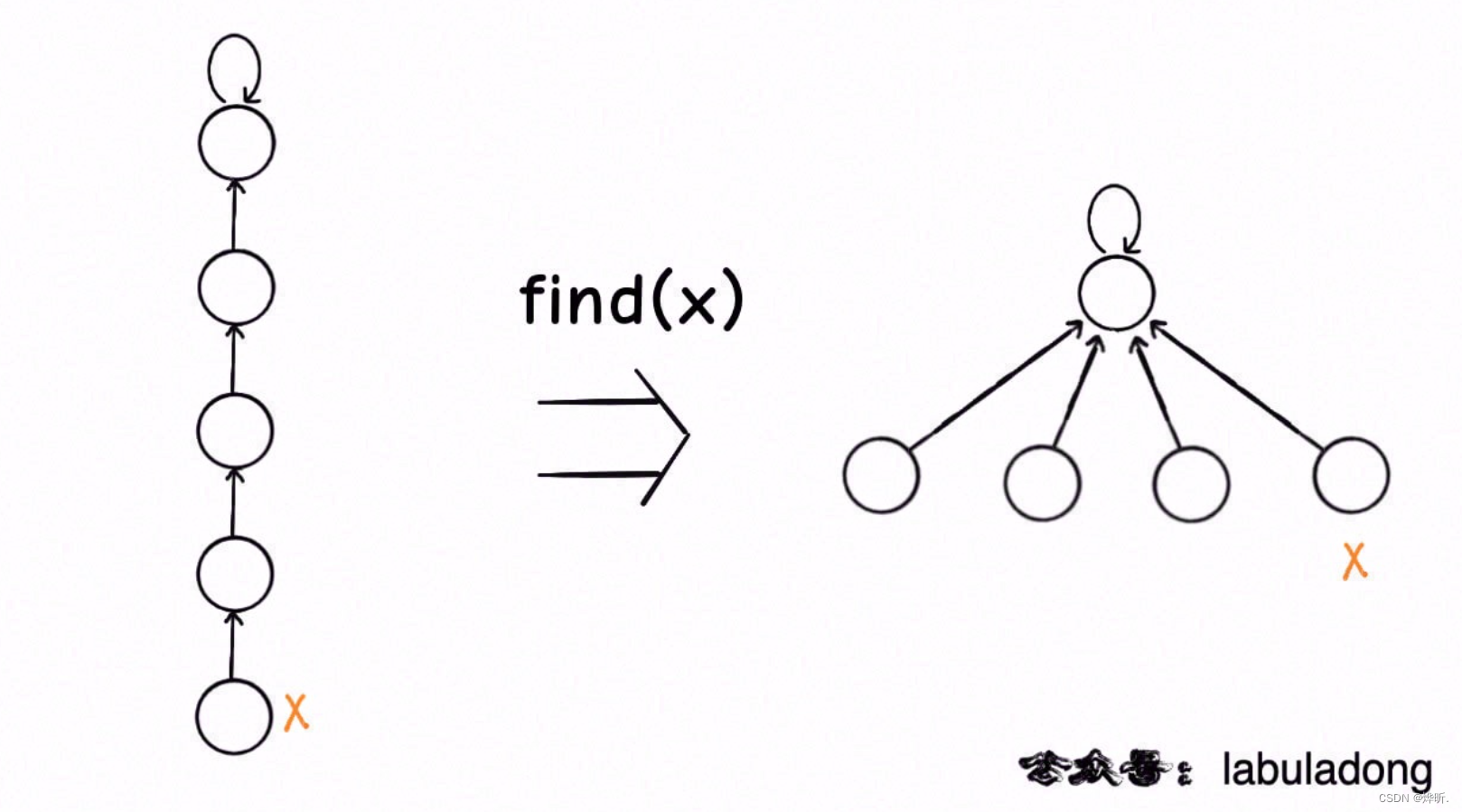
其实如果使用路径压缩技巧,那么 size 数组的平衡优化就不是特别必要了
完整代码如下:
class UF {
private:
int count = 0; // 记录连通分量
int* parent; // 节点x的父节点是parent[x]
int* size;
public:
UF(int n) {
this->count = n;
parent = new int[n];
size = new int [n];
for(int i = 0; i < n; i++) {
parent[i] = i;
size[i] = 1;
}
}
void Union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if(rootP == rootQ) return;
// 小树接到大树下面
if(size[rootP] > size[rootQ]) {
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
}else {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}
count--;
}
bool connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
int find(int x) {
// 根节点的parent[x] == x,层层向上找就好啦
if(parent[x] != x) parent[x] = find(parent[x]);
return parent[x];
}
int getCount() { return count; }
};1、用
parent数组记录每个节点的父节点,相当于指向父节点的指针,所以parent数组内实际存储着一个森林(若干棵多叉树)。2、用
size数组记录着每棵树的重量,目的是让union后树依然拥有平衡性,保证各个 API 时间复杂度为 O(logN),而不会退化成链表影响操作效率。3、在
find函数中进行路径压缩,保证任意树的高度保持在常数,使得各个 API 时间复杂度为 O(1)。使用了路径压缩之后,可以不使用size数组的平衡优化。