1 引子：猜天气小游戏

一对异地恋的情侣，女朋友想根据男友的心情猜测男友所在城市的天气

1.1 天气和心情一定一一对应

• 晴天——>高兴
• 雨天——>烦躁

 可以根据心情唯一确定天气

1.2 天气和心情没有一一对应

• 晴天——>80%高兴，20%烦躁
• 雨天——>60%高兴，40%烦躁

1.3 天气和心情没有一一对应+连续两天的天气之间有转换概率

• 天气和心情的对应关系
  • 晴天——>80%高兴，20%烦躁
  • 雨天——>60%高兴，40%烦躁
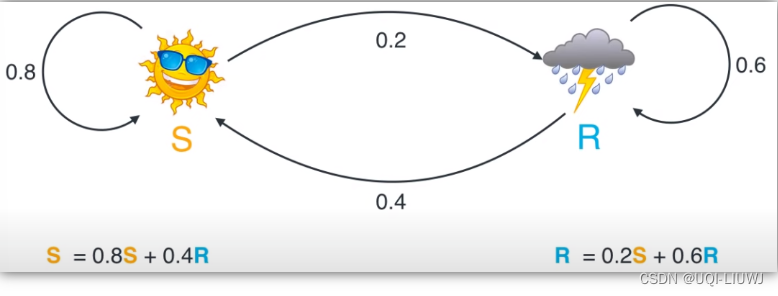
• 天气的转换概率
  • 晴天——>后一天80%的概率是晴天，20%的概率是雨天
  • 雨天——>后一天40%的概率是晴天，60%的概率是雨天

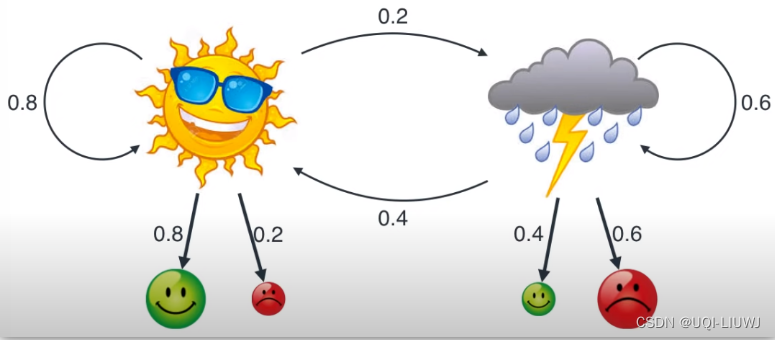
 2 HMM（hidden markov model）隐马尔科夫模型

2.1 四个重要的概念

• 观测值 observation
  • 能观测到的，心情是高兴（H）还是烦躁（G）
• 隐藏状态 hidden
  • 看不见的状态，通过观测值来推断
  • 天气时晴天（S）还是雨天（R）
• 转换概率 transition probability
  • 隐藏状态的转换概率
  • 今天晴天，明天是明天or雨天的概率，0.8/0.2
  • 今天雨天，明天是晴天or雨天的概率，0.4/0.6
  • 
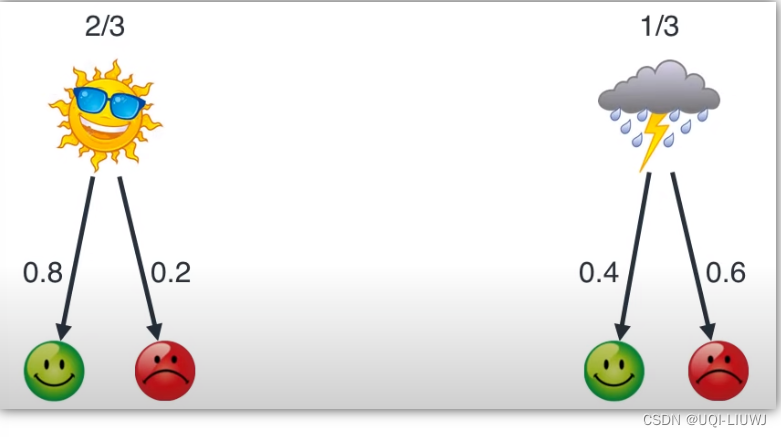
• 输出概率 emission probability
  • 从隐藏状态到观测值的概率
  • 晴天到 开心/烦躁的概率，分别是0.8/0.2
  • 雨天到 开心/烦躁的概率，分别是0.4/0.6
    • 

——>上述1.3的问题，可以写成如下的HMM形式：

 3 HMM的几个核心问题

3.1 估计转换概率和输出概率

3.1.1 转换概率

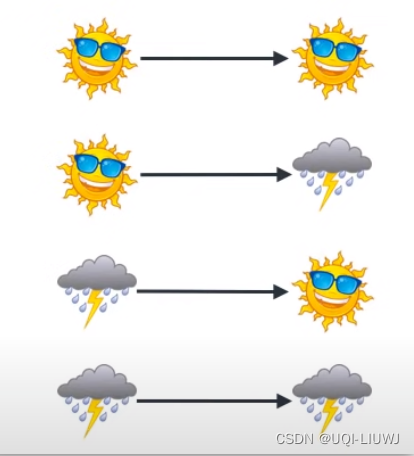
收集历史数据，统计各种天气状态转换的数量

比如收集了16天的天气：

 分别统计 （晴天->晴天，晴天——>雨天），（雨天——>雨天，雨天——>晴天）的个数，分别计算概率（每一组的概率之和为1）

3.1.2 输出概率

和3.1.1 类似，也是收集数据，通过数量统计估计概率

也是收集16天的数据：

分别统计（晴天——>高兴、晴天——>烦躁）；（雨天——>高兴、雨天——>烦躁）的个数，计算概率（每一组的概率之和为1）

 

3.2 不知道男友情绪（不知道观测值），如果估计晴天和雨天？

此时我们知道的只是隐藏状态的转换概率：

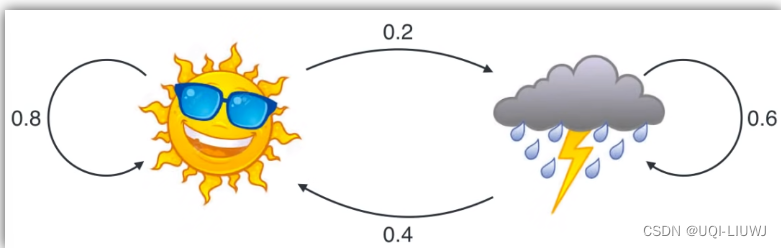
• 如果今天是晴天，那么有0.8的概率昨天是晴天，有0.4的概率昨天是雨天
  • 
• 如果今天是雨天，那么有0.6的概率昨天也是雨天，有0.2的概率昨天是晴天
  • 

• 今天只有可能是晴天或者雨天的一种，所以S+R=1
• ——>S=2/3，R=1/3，即不知道男友心情是，推断当地天气是晴天和雨天的概率分别是2/3和1/3

3.3  只考虑一天，知道男友心情，推断当地天气

• 通过3.2我们知道，不考虑心情的话，某一天有2/3的概率是晴天，1/3的概率是雨天
  • 
• 
  • ——>可以推断出，如果男友高兴，那么有8/10=4/5的概率是晴天，1/5的概率是雨天
  • ——>如果男友不高兴，那么2/5的概率是晴天，3/5的概率是雨天

3.4 知道连续几天的心情，推断连续几天的天气

3.4.1 穷举法

• 比如男友的心情是高兴-烦躁
  • 先使用穷举法列出可能的心情排列组合方式（每一天两种可能性，一共2*2=4种）
    • 
  • 以上述四种排列组合种的（晴天-雨天）为例，计算一下出现这种天气排列组合方式的概率
    • 第一天是晴天的概率：2/3【隐藏状态概率，源自于3.2】
    • 第一天是晴天，第一天心情是高兴的概率是0.8【输出概率，HMM信息】
    • 第一天是晴天，第二天是雨天的概率是0.2【转移概率，HMM信息】
    • 第二天是雨天，第二天心情是烦躁的概率是0.6【输出概率，HMM信息】
    • ——>心情是（高兴-烦躁），天气是（晴天-雨天）的概率是：
      • 2/3 * 0.8 * 0.2 * 0.6 = 0.0644
      • 
  • 穷举四种排列组合，分别计算他们的概率，概率最大的一个就是最有可能的天气组合（这里是晴天-晴天）
    • 

• 穷举法的问题是，如果需要推断连续n天的天气情况，需要2^n个排列组合结果的概率都算一遍，开销很大

 3.4.2 维特比算法

• 优化穷举法的一种算法
  • 根据第k-1步的结果，估算第k步的结果
• 比如现在的心情是高兴-高兴-烦躁-烦躁-烦躁-高兴，我们需要推断可能的天气链
  • 
  • 从第一天开始，晴天的概率是0.67，雨天的概率是0.33（3.2求得）
    • 
    • 第一天天气为晴天/雨天时，心情为高兴的概率：
      • 
      • 概率更大的晴天，可能性更大
  • 第二天
    • 再计算第二天是晴天的概率，他可能是由第一天是晴天/雨天导致的（蓝色的是转换概率，红色的是输出概率，后同）
      • 
      • 0.341大，所以SS组合的概率大于RS组合的概率
        • 
    • 第二天是雨天的概率同理：
      • 
      • 
  • 第三天
    • 第三天是晴天的概率：
      • P(G|SSS)=0.341*0.8*0.2=0.05456
      • P(G|SRS)=0.043*0.4*0.2=0.00344
    • 第三天是雨天的概率
      • P(G|SSR)=0.341*0.2*0.6=0.04092
      • P(G|SRR)=0.032*0.6*0.6=0.01152
    • ——>第三天是晴天or雨天的概率分别是0.05456，0.04092
  • 第四天
    • 第四天是晴天的概率
      • P(G|SSSS)=0.05456*0.8*0.2=0.0087
      • P(G|SSRS)=0.04092*0.4*0.2=0.0033
    • 第四天是雨天的概率
      • P(G|SSSR)=0.05456*0.2*0.6=0.0065
      • P(G|SSRR)=0.04092*0.6*0.6=0.0147
    • ——>第四天是晴天or雨天的概率分别是0.0087，0.0147
  • 第五天
    • 第五天是晴天的概率
      • P(G|SSSSS)=0.0087*0.8*0.2=0.0014
      • P(G|SSRRS)=0.0147*0.4*0.2=0.0012
    • 第五天是雨天的概率
      • P(G|SSSSR)=0.0087*0.2*0.6=0.0010
      • P(G|SSRRR)=0.0147*0.6*0.6=0.0053
    • 第五天是晴天or雨天的概率分别是0.0014，0.0053
  • 第六天
    • 第六天是晴天的概率
      • P(H|SSSSSS)=0.0014*0.8*0.8=0.00089
      • P(H|SSRRRS)=0.0053*0.4*0.8=0.0017
    • 第六天是雨天的概率
      • P(H|SSSSSR)=0.0014*0.2*0.4=0.00011
      • P(H|SSRRRR)=0.0053*0.6*0.4=0.0013
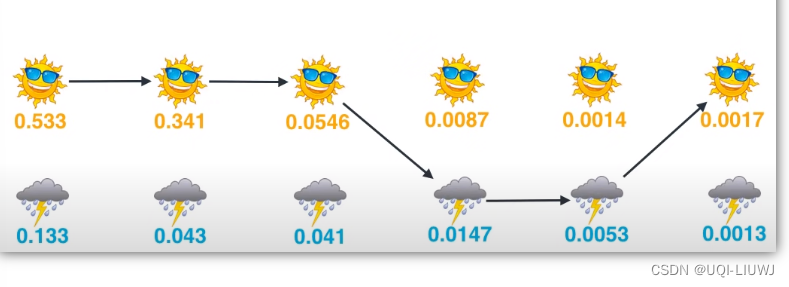
  • 沿着日期，找出每天晴天雨天概率中较大的那个，连成一条线，就是估计的天气链
    • 
• 总结一下：
  • 假设我们已经知道第k-1天是晴天or雨天的概率
  • 那么第k天是晴天or雨天的概率为
    • 第k-1天是晴天or雨天的概率*相应的转换概率*相应的第k天的输出概率
  • 

4 Python实现

4.1 数据部分 

p_s=2/3
p_r=1/3
p_init=[p_s,p_r]
#不考虑心情的话，单天晴天or雨天的概率（初始概率）

p_ss=0.8
p_sr=0.2
p_rs=0.4
p_rr=0.6
p_transition=[p_ss,p_sr,p_rs,p_rr]
#转换概率（左先右后）

p_sh=0.8
p_sg=0.2
p_rh=0.4
p_rg=0.6
p_output=[p_sh,p_sg,p_rh,p_rg]
#输出概率

observation=['H', 'H', 'G', 'G', 'G', 'H']
#男友的心情，观测值

state=['S','R']
#隐藏状态

ob_state=['H','G']
#观测状态

4.2 维特比算法

import numpy as np
def viterbi(observation,
           p_init,
           p_transition,
           p_output,
           state,
           ob_state):
    
    n_state=len(state)
    n_seq_len=len(observation)
    

    weather_prob=np.zeros((n_seq_len,n_state))
    #每个时刻不同状态的概率


    state_index=ob_state.index(observation[0])
    for i in range(n_state):
            weather_prob[0][i]=max(weather_prob[0][i],
                                       p_init[i]*\
                                      p_output[i*n_state+state_index])
    #第一天各状态的概率

        
    for i in range(1,n_seq_len):
        state_index=ob_state.index(observation[i])
        for j in range(n_state):
            for k in range(n_state):
                weather_prob[i][j]=max(weather_prob[i][j],
                                       weather_prob[i-1,k]*\
                                       p_transition[k*n_state+j]*\
                                      p_output[j*n_state+state_index])
    #后续每天各状态的概率

    weather=[]
    for i in range(n_seq_len):
        weather.append(state[np.argmax(weather_prob[i])])
    #每天的推测状态，取决于这一天概率最大的那个状态

    return weather_prob,weather

4.3 测试结果

viterbi(observation,
           p_init,
           p_transition,
           p_output,
           state,
           ob_state)
'''
(array([[0.53333333, 0.13333333],
        [0.34133333, 0.04266667],
        [0.05461333, 0.04096   ],
        [0.00873813, 0.0147456 ],
        [0.0013981 , 0.00530842],
        [0.00169869, 0.00127402]]),
 ['S', 'S', 'S', 'R', 'R', 'S'])
'''

参考内容：小孩都看得懂的 HMM (qq.com)