前言

二叉树有前中后序和层序四种常用的遍历方式，今天我们来学习一下如何用这四种方法遍历二叉树。
前序：根、左、右
中序：左、右、根
后序：左、右、根
层序：第一层、第二层…

递归

递归是一种将复杂问题不断细分成小问题的方法。
既然是划分大问题为小问题，就要考虑明白什么时候是最小的问题，也就是我们常说的终止条件，就拿前序遍历举例子：
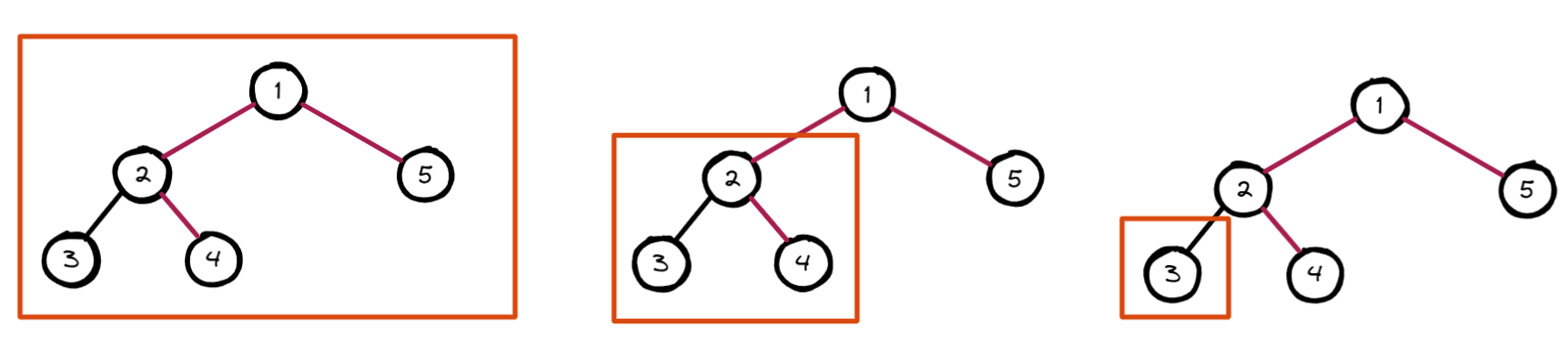
前序遍历要求我们按根、左、右的顺序去访问树，那我们访问完根节点，就可以将问题转换为子问题去访问他的左子树了。
当访问完根节点，再去访问根的左节点，当这个根的左节点访问完毕，最后去访问根的右节点，当遇到空的时候就终止。
在这里插入图片描述

前序

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        Traversal(root,result);
        return result;
    }

    void Traversal(TreeNode* cur,vector<int>& result){
        if(cur == NULL){
            return; 
        }
        result.push_back(cur->val);      
        Traversal(cur->left, result);
        Traversal(cur->right, result);
    }
};

中序

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        Traversal(root,result);
        return result;
    }

    void Traversal(TreeNode* cur,vector<int>& result){
        if(cur == NULL){
            return; 
        }     
        Traversal(cur->left, result);
        result.push_back(cur->val);
        Traversal(cur->right, result);
        
    }
};

后序

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
        Traversal(root,result);
        return result;
    }

    void Traversal(TreeNode* cur,vector<int>& result){
        if(cur == NULL){
            return; 
        }
              
        Traversal(cur->left, result);
        Traversal(cur->right, result);
        result.push_back(cur->val);
    }
};

非递归

递归算法简单易懂，但是递归是要开辟栈帧的，栈的大小一般只有8M左右大小，递归调用层数太深很容易爆栈，因此我们还要学习如何通过非递归的方式进行遍历二叉树

非递归遍历也是大事化小的思想，拿前序遍历来讲，即先将左路节点全部入栈，root的所有左路节点入栈后，再进入到栈顶元素的右树(如果有的话),重复这个过程，即完成了前序遍历。

前序

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        //前序遍历：根、左、右
        stack<TreeNode*> st;
        vector<int> v;

        TreeNode* cur = root;
        while(cur || !st.empty())
        {
            //开始访问一棵树
            //1.左路节点
            //2.左路节点的右子树
            while(cur)
            {
                v.push_back(cur->val);
                st.push(cur);
                cur = cur->left;
            }

            //开始访问右子树
            TreeNode* top = st.top();
            st.pop();

            //访问右子树，转换为子问题
            cur = top->right;
        }

        return v;
    }
};

中序
中序要按照左、根、右的方式遍历一棵树，还是一样一路并入root的左路节点，直到子问题变成左树为空的节点，这样直接将这个节点读取，再走他的右树(如果有右树的话)，重复上面的逻辑即可。

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        //中序：左 根 右
        stack<TreeNode*> st;
        vector<int> v;

        TreeNode* cur = root;
        while(cur || !st.empty())
        {
            while(cur)
            {
                st.push(cur);
                cur = cur->left;
            }

            //加入节点，因为左边一定是空了
            TreeNode* top = st.top();
            st.pop();
            v.push_back(top->val);
            
            //去右树
            cur = top->right;
        } 

        return v;
    }
};

后序
后序与前面两者略有不同，后序在什么时候能够读取节点呢？必须在左右树(节点)都访问完成后才可以访问根节点，我们是将左路节点一路压到栈里的，由于栈先进后出，也就是说走到任意一个节点，必然已经走过了他的左路节点。
如果右树不存在，我们自然可以直接访问这个节点，但如果右树存在，我们还是要按照刚开始的步骤压入左路节点，这样肯定在这颗右树处理完毕后再访问到这个节点，这时候左右树都已访问完毕，可以访问这颗树了，因此需要一个指针来记录我们上个元素访问的是谁，如果是这个节点的右子树的话，就可以访问这个节点。

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        //后序：左 右 根
        stack<TreeNode*> st;
        vector<int> v;

        TreeNode* cur = root;
        TreeNode* prev = nullptr;
        while(cur || !st.empty())
        {
            while(cur)
            {
                st.push(cur);
                cur = cur->left;
            }

            TreeNode* top = st.top();
            if(top->right == nullptr || top->right == prev)
            {
                v.push_back(top->val);
                st.pop();

                prev = top;
            }
            else
            {
                cur = top->right;
            }
        }

        return v;
    }
};

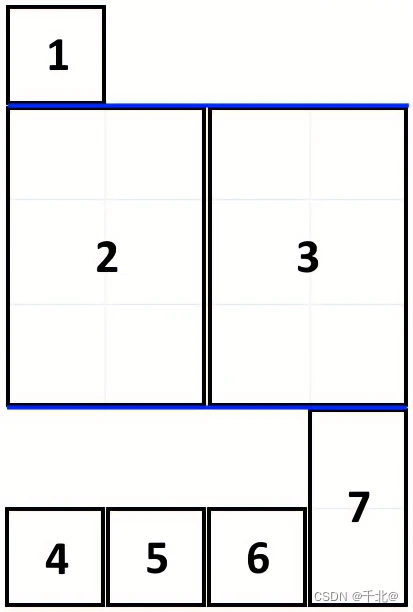
层序遍历

层序遍历就是一层一层遍历二叉树，如图：
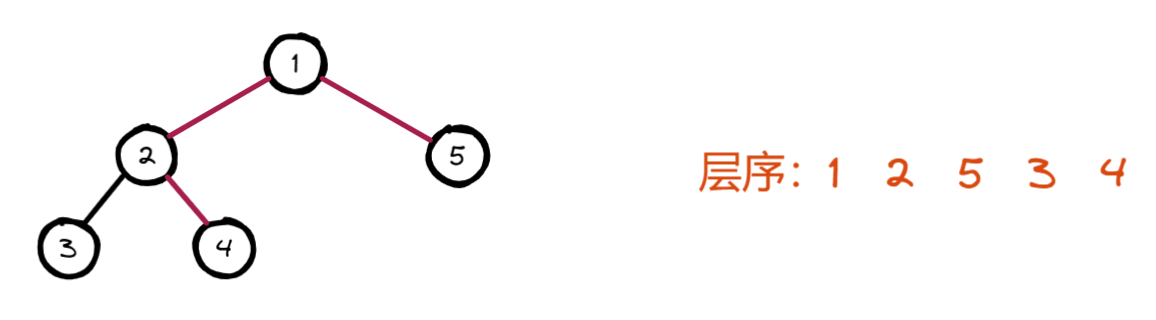
在这里插入图片描述
要实现层序遍历我们要借助栈的数据结构，基本思路为：
先将根节点压入栈，访问完一个节点就将这个节点的子节点都入队列(如果有的话)，以此类推，每次出队都会带来两个入队列。这一层出完，剩下的就都是下一层的了。

class Solution{
public:
    vector<vector<int>> levelOrder(TreeNode* root){
        vector<vector<int>> vv;
        int levelSzie = 0;/*表示当前层有多少个元素*/
        
        queue<TreeNode*> que;
        if(root)
        {
            que.push(root);
            levelSzie = 1;
        }
        while(!que.empty())
        {
            vector<int> v;
            while(levelSzie--)
            {
                TreeNode* node = que.front();
                que.pop();

                v.push_back(node->val);

                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
            vv.push_back(v);
            levelSzie = que.size();
        }

        return vv;
    }
};