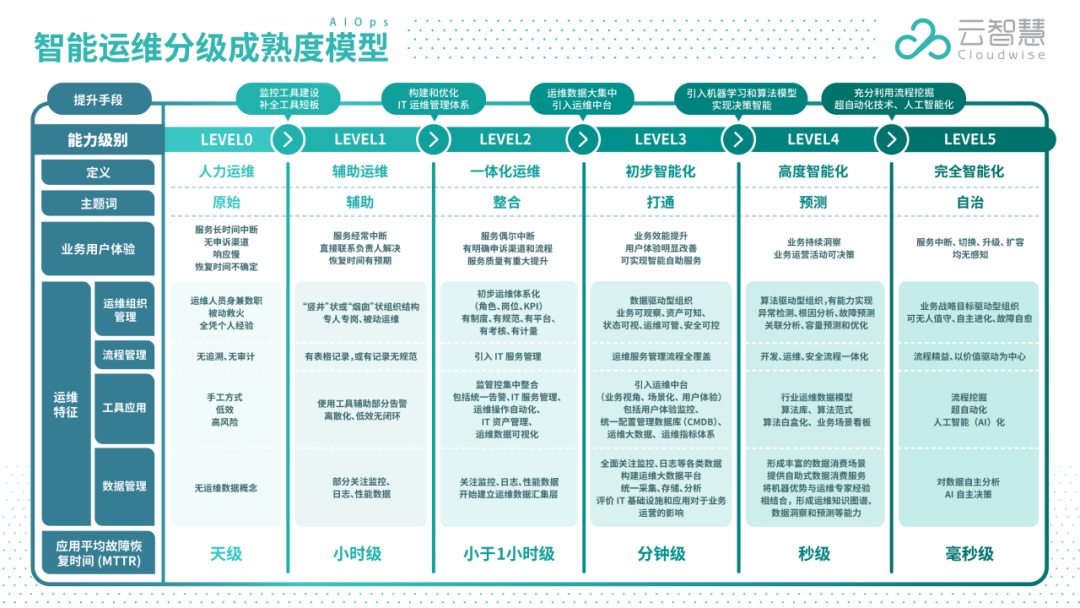
来源：力扣（LeetCode）

描述：

给定一个数组 books ，其中 books[i] = [thicknessi, heighti] 表示第 i 本书的厚度和高度。你也会得到一个整数 shelfWidth 。

按顺序 将这些书摆放到总宽度为 shelfWidth 的书架上。

先选几本书放在书架上（它们的厚度之和小于等于书架的宽度 shelfWidth ），然后再建一层书架。重复这个过程，直到把所有的书都放在书架上。

需要注意的是，在上述过程的每个步骤中，摆放书的顺序与你整理好的顺序相同。

• 例如，如果这里有 5 本书，那么可能的一种摆放情况是：第一和第二本书放在第一层书架上，第三本书放在第二层书架上，第四和第五本书放在最后一层书架上。

每一层所摆放的书的最大高度就是这一层书架的层高，书架整体的高度为各层高之和。

以这种方式布置书架，返回书架整体可能的最小高度。

示例 1：

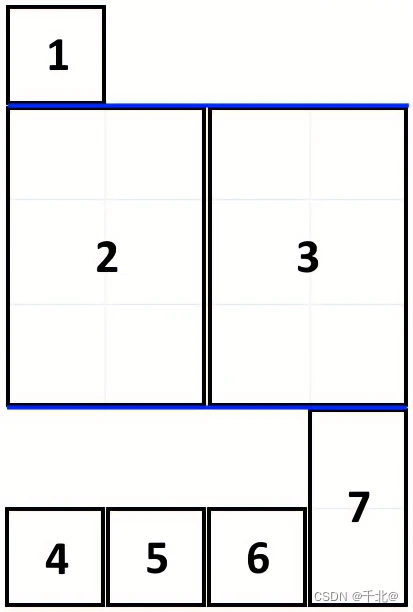
输入：books = [[1,1],[2,3],[2,3],[1,1],[1,1],[1,1],[1,2]], shelfWidth = 4
输出：6
解释：
3 层书架的高度和为 1 + 3 + 2 = 6 。
第 2 本书不必放在第一层书架上。

示例 2:

输入: books = [[1,3],[2,4],[3,2]], shelfWidth = 6
输出: 4

提示：

• 1 <= books.length <= 1000
• 1 <= thicknessi <= shelfWidth <= 1000
• 1 <= heighti <= 1000

方法：动态规划

思路与算法

根据题意，按顺序将这些书摆放到总宽度为 shelfWidth 的书架上。先选几本书放在书架上，然后再建一层书架。重复这个过程，直到把所有的书都放在书架上。

考虑用「动态规划」来解决这个问题，dp[i] 来表示放下前 i 本书所用的最小高度。 因为最多 1000 本书， 每本书高度最大 1000，我们可以把 dp[i] 初始化为 1000000， 初始化 dp[0] 为零，表示没有书是高度为零。

当我们要放置前 i 本书时候，假定前 j 本书放在上面的书架上，其中 j < i, 前 j 本书放好后剩余的书放在最后一层书架上, 这一层书架的高度是这部分书的高度最大值，由此得到如此递推公式：

dp[i] = min(dp[j] + max(books[k]))
其中满足 0 ≤ j ≤ k < i ≤ n, ∑books[k] ≤ shelfWidth
我们循环遍历 i, 求出 dp[i] 的值，最后返回 dp[n] 为最终答案。

代码：

class Solution {
public:
    int minHeightShelves(vector<vector<int>>& books, int shelfWidth) {
        int n = books.size();
        vector<int> dp(n + 1, 1000000);
        dp[0] = 0;
        for (int i = 0; i < n; ++i) {
            int maxHeight = 0, curWidth = 0;
            for (int j = i; j >= 0; --j) {
                curWidth += books[j][0];
                if (curWidth > shelfWidth) {
                    break;
                }
                maxHeight = max(maxHeight, books[j][1]);
                dp[i + 1] = min(dp[i + 1], dp[j] + maxHeight);
            }
        }
        return dp[n];
    }
};

执行用时：0 ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗：7.8 MB, 在所有 C++ 提交中击败了83.69%的用户
复杂度分析
时间复杂度：O(n²)，其中 n 是 books 的长度。
空间复杂度：O(n)，其中 n 是 books 的长度。
author：LeetCode-Solution