凸多边形的划分

题目描述

给定一个具有N个顶点的凸多边形，将顶点从1至N标号，每个顶点的权值都是一个正整数。将这个凸多边形划分成N-2个互不相交的三角形，试求这些三角形顶点的权值乘积和至少为多少。

输入描述

输入第一行为顶点数N第二行依次为顶点1至顶点N的权值。

输出描述

输出仅一行，为这些三角形顶点的权值乘积和的最小值。

样例

5
121 122 123 245 231

12214884

说明

• 对于100% 的数据，有 $N\le 50$ ，每个点权值小于 $10^9$ 。
• https://ac.nowcoder.com/acm/problem/50500

解析

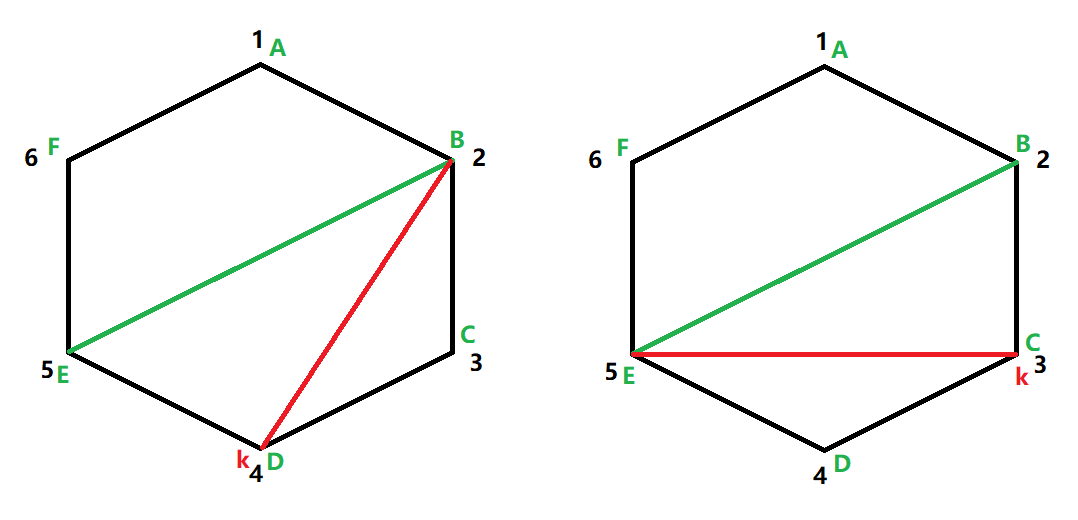
按照以往的套路，题目要求说明，我们就做什么假设，假设 $[i,j]$ 为最小划分三角形。

以 BE （$[2,5]$）为例，以 BE 为固定边做辅助线，可作出 BD 或 EC，分别可以划分三角形为 EBD 与 BDC 或 BEC 和 CED，其中划分的点 D 与 C 称为分界点 K。

可得方程：
$$dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]+A[i]\ast A[j]\ast A[k])$$
初始化：

• $dp[i][j]=INF$

代码

以下代码只能获得 40 分（方便理解DP过程）

public class Main {
    static final int INF = 1 << 30;
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[] A = new int[n+1];
        long[][] dp = new long[n+1][n+1];
        for(int i = 1; i <= n; i++) A[i] = sc.nextInt();
        for(int len = 3; len <= n; len++) {
            for(int i = 1; i + len - 1 <= n; i++) {
                int j = i + len - 1;
                dp[i][j] = INF;
                for(int k = i + 1; k < j; k++) {
                    dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j] + (A[i] * A[j] * A[k]));
                }
            }
        }
        System.out.println(dp[1][n]);
    }
}

AC 代码

public class Main {
    static BigInteger INF = new BigInteger("1000000000000000000000000000");
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        
        BigInteger[] A = new BigInteger[n+1];
        BigInteger[][] dp = new BigInteger[n+1][n+1];
        
        for(int i = 1; i <= n; i++) Arrays.fill(dp[i], new BigInteger("0"));
        for(int i = 1; i <= n; i++) A[i] = new BigInteger(sc.nextInt() + "");
        
        for(int len = 3; len <= n; len++) { // 枚举区间
            for(int i = 1; i + len - 1 <= n; i++) { // 枚举区间起点
                int j = i + len - 1; // 计算区间终点
                dp[i][j] = INF;
                for(int k = i + 1; k < j; k++) { // 枚举分界点
                    BigInteger a = dp[i][j];
                    BigInteger t = new BigInteger("0");
                    if(dp[i][k] != null) t = t.add(dp[i][k]);
                    if(dp[k][j] != null) t = t.add(dp[k][j]);
                    if(A[i] != null && A[j] != null && A[k] != null) t = t.add(A[i].multiply(A[j]).multiply(A[k]));
                    if(a.compareTo(t) >= 1) dp[i][j] = t;
                }
            }
        }
        
        System.out.println(dp[1][n]);
    }
}