快速排序

【思想】选择一个元素作为标准，分别将小于该元素的元素放入该元素左边，大于该元素的元素放到该元素的右边，接下来分别对左右两边区间进行同样操作，直到整个数组有序。

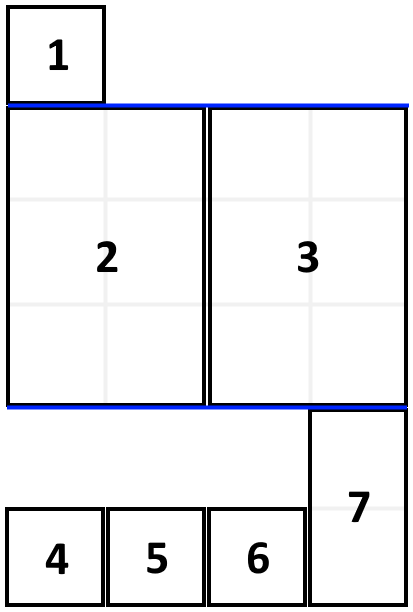
【例子】

上述是一个未排序的数组，首先选择一个元素作为切分元素（下图中选择元素4），将小于切分元素的放到左边，大于切分元素的放到右边，最终我们确定了一个元素（4）排完序之后的最终位置，这个过程称为partition。


接下来就是分别对左边和右边的区间以此进行同样的操作，直到完成整个数组的排序。

【partition详细实现步骤】

PS: 在划分过程中，左边表示小于（等于）切分元素的区间，右边是大于（等于）切分元素的区间。

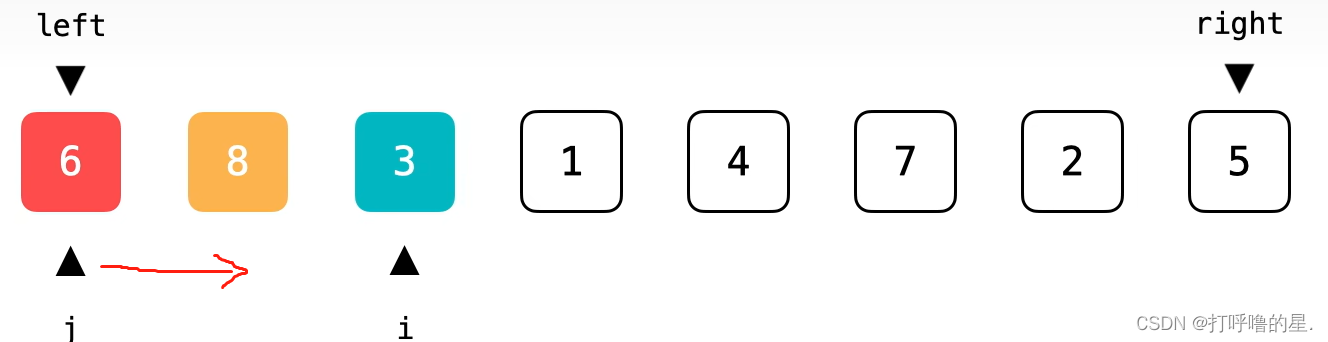
【step1】一般选择数组中的第一个元素为切分元素pivot，然后遍历数组进行比较。下图中i用来遍历数组，j用来表示第一个区间（小于切分元素的区间）的最后一个位置。

【step 2】当前元素(i指向的元素)小于等于pivot时，继续向前，i=i+1；当大于pivot时，j+1，然后交换位置j和i对应的元素。


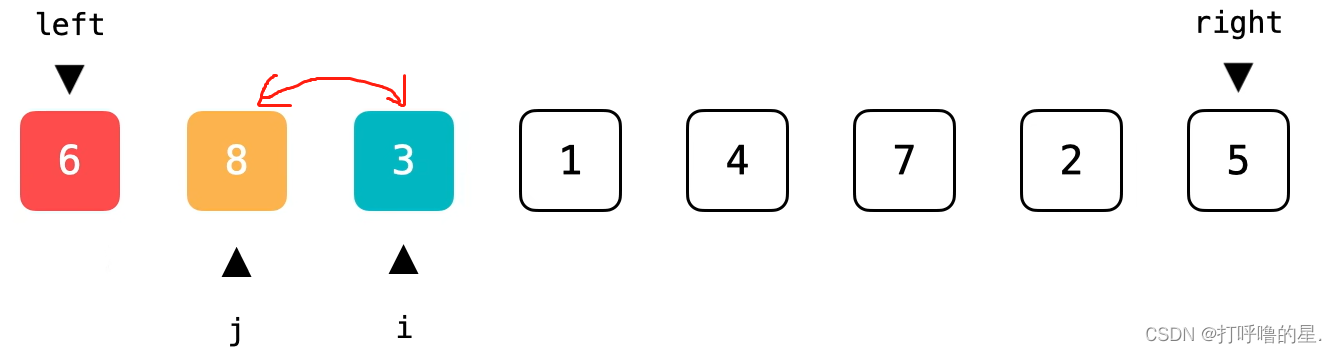
【step3】进行到下图时，表示已经把6后面的元素分为两个区间，左边是小于（等于）该元素的nums[left, j]，右边是大于该元素的nums[j+1, right]。最后将j指向的元素和left指向元素交换位置，完成区间的划分。
ps：j指向第一个区间（小于切分元素区间）的最后一个位置。

【代码实现】

import random
class Solution:
    def sortArray(self, nums: List[int]) -> List[int]:
        self.quickSort(nums, 0, len(nums)-1)
        return nums

    def quickSort(self, nums, left, right):
        if left >= right:
            return

        pivot_index = self.partition(nums, left, right)
        self.quickSort(nums, left, pivot_index-1)
        self.quickSort(nums, pivot_index +1, right)

    def partition(self, nums, left, right):
        index = left + random.randint(0, (right-left))
        self.swap(nums, left, index)
        pivot = nums[left]
        for i in range(left+1, right+1):
        	if nums[i] > pivot:
        		j += 1
        		self.swap(nums, i, j)
        self.swap(nums, left, j)#最终交换第一个元素和j指向元素
		return j    
    def swap(self, nums, index1, index2):
        nums[index1], nums[index2] = nums[index2], nums[index1]

PS：上述partition中，之所以随机选取一个元素和第一个元素进行交换，是因为当元素本身有序（顺序或者逆序）时，每次partition进行遍历的元素个数只比上次少了一个，时间复杂度为O(N^2)。即：partition在有序数组上表现很差，因此用随机选择来打破这种平衡。

快速排序之双路快排

【引入】当数组中重复元素较多时，如果随机选择元素与pivot相等的概率较大，相同元素进行交换是没有意义的。

极端的情况：当元素都相等时，随机选择pivot无效！

【解决方法】
（1）双路快排：把与pivot相等的元素平均分到数组的两侧。

（2）三路快排：把与pivot相等元素挤到中间。

【双路快排】
最终划分区间满足：左边区间nums[left, le)<=pivot：小于等于pivot，右边区间(ge, right]>=pivot
在遍历过程中，le指向左边区间右边界的后一个位置，用ge指向右边区间左边界的前一个位置

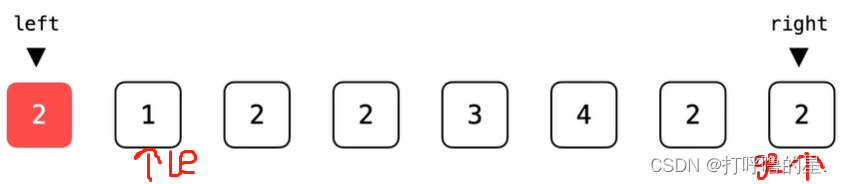
当le遇到大于等于pivot元素停下来，ge遇到小于等于pivot元素停下来
然后交换对应元素

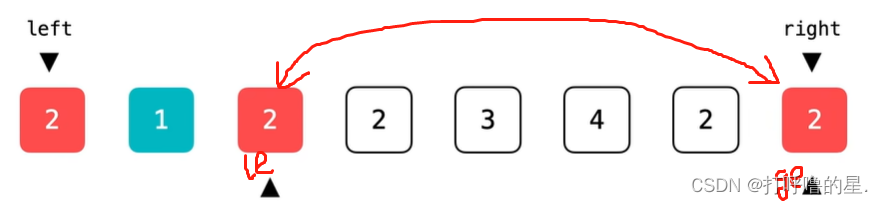
最后要注意partition遍历结束后left要和le还是ge交换位置？

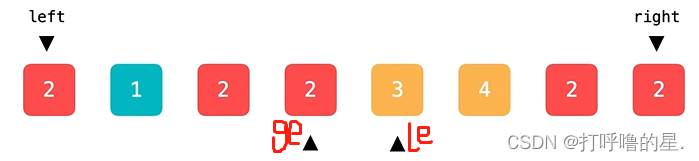
跳出循环后，le和ge有两种情况:（1）le = ge（2）ge>le

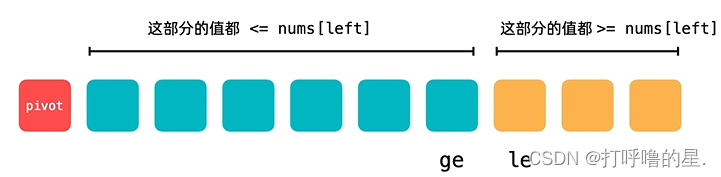
根据上述可知，le、ge停下来分别指向大于等于pivot的元素，和小于等于pivot的元素。
（1）当两者重合时，le和ge指向同一个元素，pivot与交换le和ge均可。
（2）如果不重合，如果pivot与le进行交换，就可能将大于pivot的元素交换到第一个区间里，这是错误的。
因此最终应与ge交换位置来适应以上两种情况。

【代码实现】

def partition(self, nums, left, right):
        index = left + random.randint(0, (right-left))
        self.swap(nums, left, index)
        pivot = nums[left]
        le = left + 1
        ge = right
        while True:
        	#此处注意下方and左右两个条件顺序不能换，否则会出现数组越界。
            while le <= ge and nums[le] < pivot:
                le += 1
            while le <= ge and nums[ge] > pivot:
                ge -= 1
            #此时le来到第一个大于等于pivot位置
            #此时ge指向第一个小于等于pivot位置
            if le >= ge:
                break
            self.swap(nums, le, ge)
            le += 1
            ge -= 1
        self.swap(nums, left, ge)
    #返回第一个区间最后一个元素的位置（经过partion后进行确定的位置）
        return ge

快速排序之三路快排

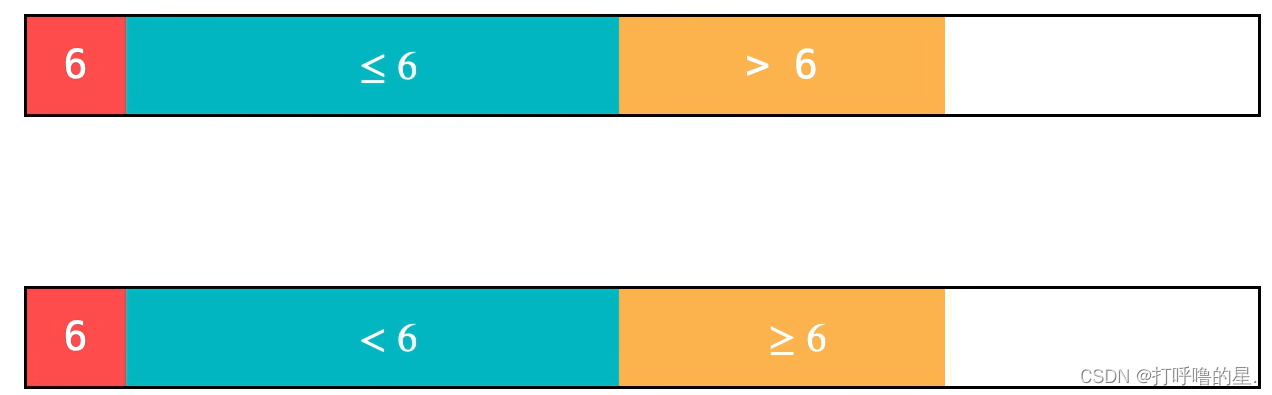
【思想】将与切分元素pivot相等的值挤到数组中间。（下图中假设pivot=6）

【实现细节】最终划分为三个区间：第一个区间：严格小于pivot区间，第二个区间：等于pivot区间，第三个区间：严格大于pivot区间。
为实现上述区间划分，用i进行将切分元素pivot后面元素进行遍历，根据当前元素与pivot大小分为三种情况：
（1）nums[i]<pivot，应划分到第一个区间，即将等于pivot区间的第一个位置进行交换（此时第一个区间多了一个单位）。

（2）nums[i]=pivot, 继续向前遍历。
（3）nums[i] > pivot, 应划分到第三个区间，将严格大于pivot区间的第一个位置的前一个位置进行交换（此时第三个区间多了一个单位）。

继续看当前元素位置的值与 pivot大小。
PS: 最后将切分元素和第一个区间的最后一个位置进行交换。
【概括】经过三路快排的数组如下图，将元素值相同的元素挤到中间确定了更多元素的位置，接下来递归处理的区间大大减小。

【例子】

（1）初始化

left，right分别表示整个区间的开始和结束。

pivot = nums[left], 选择第一个元素为切分元素。
lt = left + 1
gt = right
i = left + 1
nums[left+1, lt) < pivot， lt是第一个区间最后位置的下一个位置，也是第二个区间的第一个位置
nums[lt, i) == pivot，i表示当前元素，还未进行比较。
nums(gt, right] > pivot， gt表示第三个区间第一个位置的前一个位置。

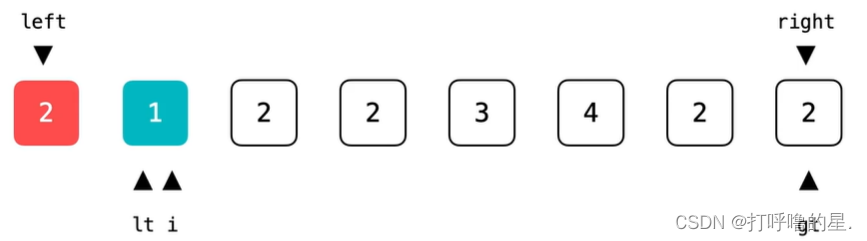
(2)交换过程示例

当nums[i] < pivot时，

应该在第一个区间，因此将pivot与第一个区间的下一个位置(lt)进行交换。

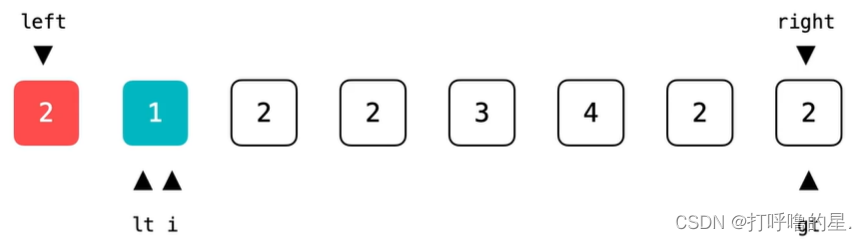
交换后：lt向前移一位，i也向前移一位。

当nums[i] > pivot,

nums[i]应该属于第三个区间，因此，将第三个区间第一个位置的前一个位置（gt）进行交换。

交换后：gt向前移动一位，i不移动。

（3）循环终止

此时，循环终止，表示i看完了left后面的所有元素。

最后将切分位置元素与第一个区间里的最后一个位置（lt-1）进行交换，完成区间划分

【三路快排实现代码】

import random
class Solution:
    def sortArray(self, nums: List[int]) -> List[int]:
        self.quickSort(nums, 0, len(nums)-1)
        return nums

    def quickSort(self, nums, left, right):
        if left >= right:
            return
        #三路快排每次确定两个位置 ，将遍历空间划分为三个区间，
        #三个区间需要有两个分界位置，因此每次partition返回两个元素
        index = left + random.randint(0, (right-left))
        self.swap(nums, left, index)
        pivot = nums[left]
        #nums[left, lt) < pivot
        #lt是第一个区间最后位置的下一个位置，也是第二个区间的第一个位置
        #nums[lt, i) = pivot
        #nums(gt, right] > pivot gt是最后一个区间第一个位置的前一个位置
        lt = left + 1
        gt = right
        i = left + 1
        while i <= gt:
            if nums[i] < pivot:
                #将nums[i]与第二个区间的第一个元素进行交换
                self.swap(nums, i, lt)
                lt += 1
                i += 1
            elif nums[i] > pivot:
                self.swap(nums, i, gt)
                gt -= 1
                #此时i不移动，因为交换后的元素需要让下一轮看到
            else:
                i += 1

        #将切分元素交换到对应位置
        self.swap(nums, left, lt - 1)

        self.quickSort(nums, left, lt-2)
        self.quickSort(nums, gt + 1, right)    
        
    def swap(self, nums, index1, index2):
        nums[index1], nums[index2] = nums[index2], nums[index1]

---

参考：B站https://space.bilibili.com/236935093/channel/collectiondetail?sid=378477。