机器学习——主成分分析法（PCA）

一、主成分分析的概念

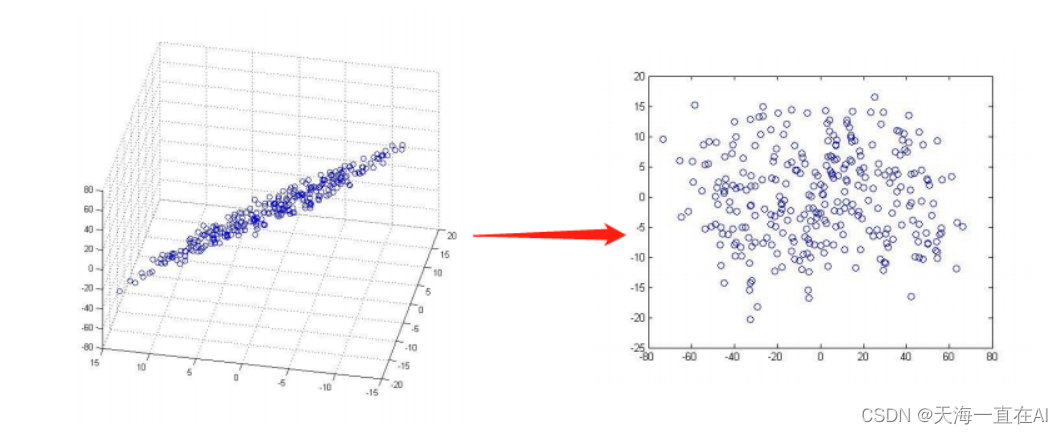
主成分分析（PCA）是一种常用的数据降维方法，可以将高维数据转换为低维空间，同时保留原始数据中最具代表性的信息。在数学建模中，PCA可以应用于多个领域，例如金融、医学、自然语言处理等。
$$x\in {\mathbb{R}}^2⟶z\in \mathbb{R}$$
在实际的数学建模中，降维操作是很常用的。

比如在图像处理中，如果要识别人脸，需要将每张图像表示为一个向量，每个元素代表图像中某个像素点的灰度值。由于每张图像的像素数量很大，可能成百上千万甚至更多，这会导致计算和存储成本非常高。

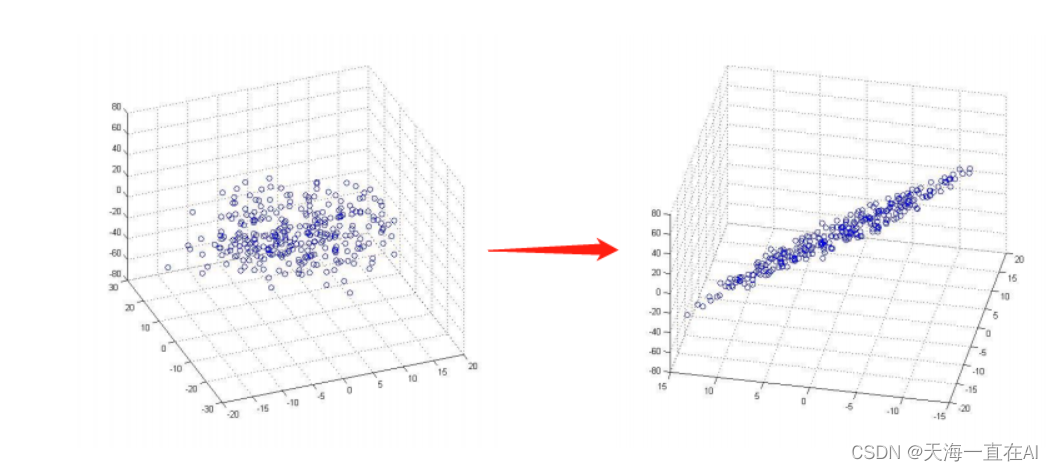
在这种情况下，可以使用PCA对这些向量进行降维，将每张图像表示为一个包含较少元素的向量，从而使得计算和存储成本大大降低。同时，PCA还能够从这些低维向量中提取出最具代表性的信息，以便于后续s的人脸识别任务。

二、主成分分析的步骤

1、数据预处理

中心化
$$X-\bar{X}$$
2、求样本的协方差矩阵
$$\frac{1}{m}X{X}^T$$
其中协方差描述两个数据的相关性，接近1为正相关，接近-1为负相关，接近0为不相关。两个数据的协方差计算公式如下：
$$cov(X,Y)=\frac{{\sum }_{i=1}^n(X_i-\bar{X})(Y_i-\bar{Y})}{n-1}$$
3、对协方差矩阵做特征值分解

4、选出最大的K个特征值对应的K个特征向量

5、将原始数据投影到选取的特征向量上

6、输出投影后的数据集

三、主成分分析PCA的简单实现

首先我们有一个二维数据长这样

32.50234527	31.70700585
53.42680403	68.77759598
61.53035803	62.5623823
47.47563963	71.54663223
59.81320787	87.23092513
55.14218841	78.21151827
52.21179669	79.64197305
39.29956669	59.17148932
48.10504169	75.3312423
52.55001444	71.30087989

我们需要将这个二维数据变为一维数据

代码如下：

1、首先载入数据查看我们数据的分布情况

import numpy as np
import matplotlib.pyplot as plt

data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:,0]
y_data = data[:,1]
plt.scatter(x_data,y_data)
plt.show()
print(x_data.shape)

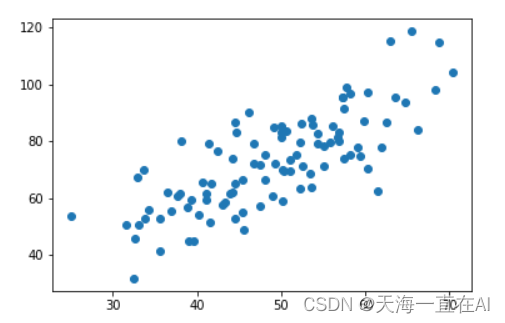
对应上面的步骤和公式，将数据中心化

def zeroMean(dataMat):
    # 按列求平均，即各个特征的平均
    meanVal = np.mean(dataMat, axis=0) 
    newData = dataMat - meanVal
    return newData, meanVal

2、求协方差矩阵

newData,meanVal=zeroMean(data)  
# np.cov用于求协方差矩阵，参数rowvar=0说明数据一行代表一个样本
covMat = np.cov(newData, rowvar=0)

3、求矩阵的特征值和特征向量

eigVals, eigVects = np.linalg.eig(np.mat(covMat))

4、对特征值排序

eigValIndice = np.argsort(eigVals)

5、取最大的top个特征值下标

n_eigValIndice = eigValIndice[-1:-(top+1):-1]

最大的n个特征值对应的特征向量

n_eigVect = eigVects[:,n_eigValIndice]
lowDDataMat = newData*n_eigVect
reconMat = (lowDDataMat*n_eigVect.T) + meanVal

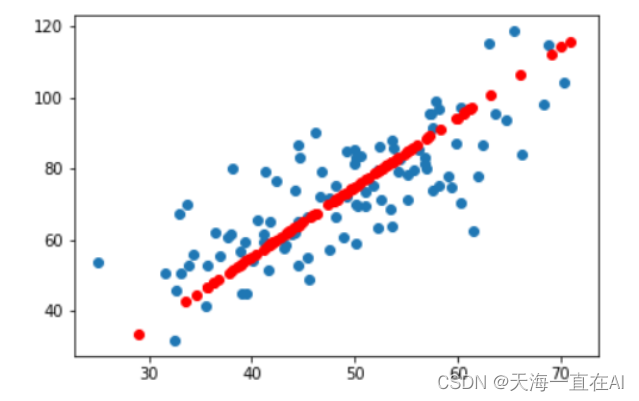
6、特征空间的数据

data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:,0]
y_data = data[:,1]
plt.scatter(x_data,y_data)

# 重构的数据
x_data = np.array(reconMat)[:,0]
y_data = np.array(reconMat)[:,1]
plt.scatter(x_data,y_data,c='r')
plt.show()

四、手写体识别数字降维

引入sklearn中的手写数字识别

from sklearn.neural_network import MLPClassifier
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report,confusion_matrix
import numpy as np
import matplotlib.pyplot as plt

接下来代码如下

digits = load_digits()#载入数据
x_data = digits.data #数据
y_data = digits.target #标签

x_train,x_test,y_train,y_test = train_test_split(x_data,y_data) #分割数据1/4为测试数据，3/4为训练数据
mlp = MLPClassifier(hidden_layer_sizes=(100,50) ,max_iter=500)
mlp.fit(x_train,y_train)
# 数据中心化
def zeroMean(dataMat):
    # 按列求平均，即各个特征的平均
    meanVal = np.mean(dataMat, axis=0) 
    newData = dataMat - meanVal
    return newData, meanVal

def pca(dataMat,top):
    # 数据中心化
    newData,meanVal=zeroMean(dataMat) 
    # np.cov用于求协方差矩阵，参数rowvar=0说明数据一行代表一个样本
    covMat = np.cov(newData, rowvar=0)
    # np.linalg.eig求矩阵的特征值和特征向量
    eigVals, eigVects = np.linalg.eig(np.mat(covMat))
    # 对特征值从小到大排序
    eigValIndice = np.argsort(eigVals)
    # 最大的n个特征值的下标
    n_eigValIndice = eigValIndice[-1:-(top+1):-1]
    # 最大的n个特征值对应的特征向量
    n_eigVect = eigVects[:,n_eigValIndice]
    # 低维特征空间的数据
    lowDDataMat = newData*n_eigVect
    # 利用低纬度数据来重构数据
    reconMat = (lowDDataMat*n_eigVect.T) + meanVal
    # 返回低维特征空间的数据和重构的矩阵
    return lowDDataMat,reconMat 
lowDDataMat,reconMat = pca(x_data,2)
# 重构的数据
x = np.array(lowDDataMat)[:,0]
y = np.array(lowDDataMat)[:,1]
plt.scatter(x,y,c='r')
plt.show()
predictions = mlp.predict(x_data)
# 重构的数据
x = np.array(lowDDataMat)[:,0]
y = np.array(lowDDataMat)[:,1]
plt.scatter(x,y,c=y_data)
plt.show()
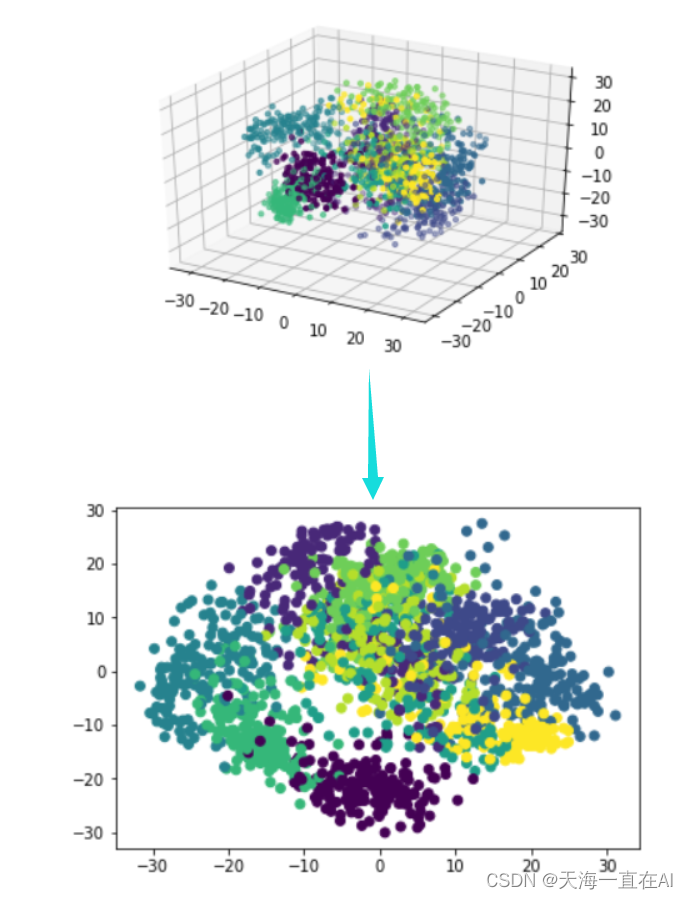
lowDDataMat,reconMat = pca(x_data,3)
from mpl_toolkits.mplot3d import Axes3D  
x = np.array(lowDDataMat)[:,0]
y = np.array(lowDDataMat)[:,1]
z = np.array(lowDDataMat)[:,2]
ax = plt.figure().add_subplot(111, projection = '3d') 
ax.scatter(x, y, z, c = y_data, s = 10) #点为红色三角形 
plt.show()