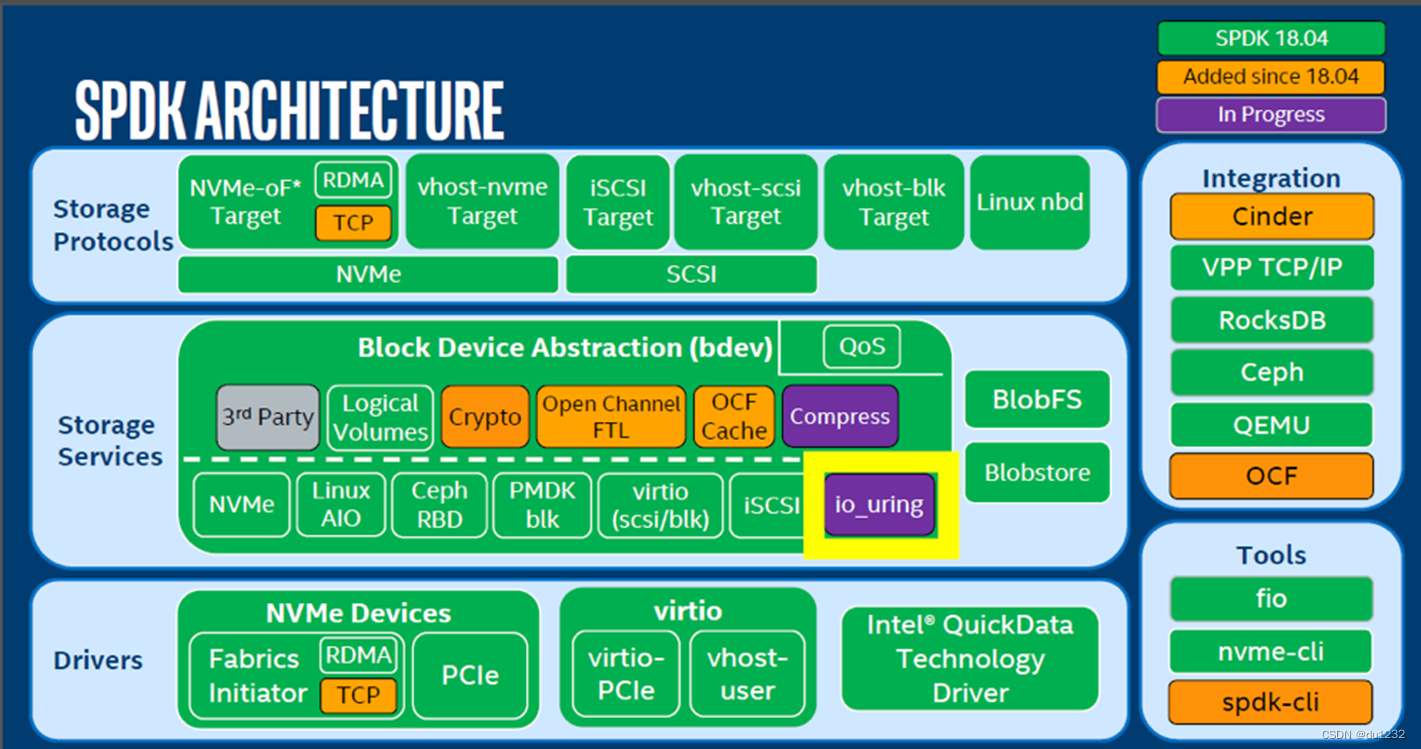
https://codeforces.com/contest/1714/problem/D

题目大意

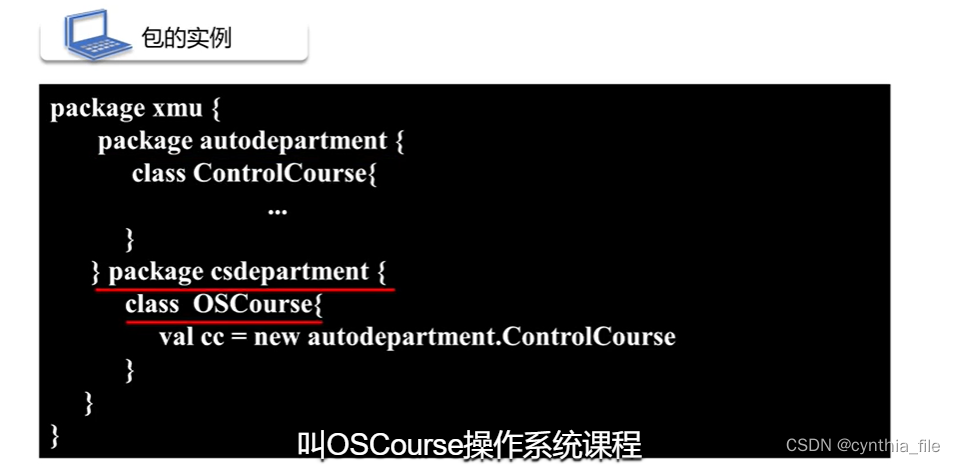
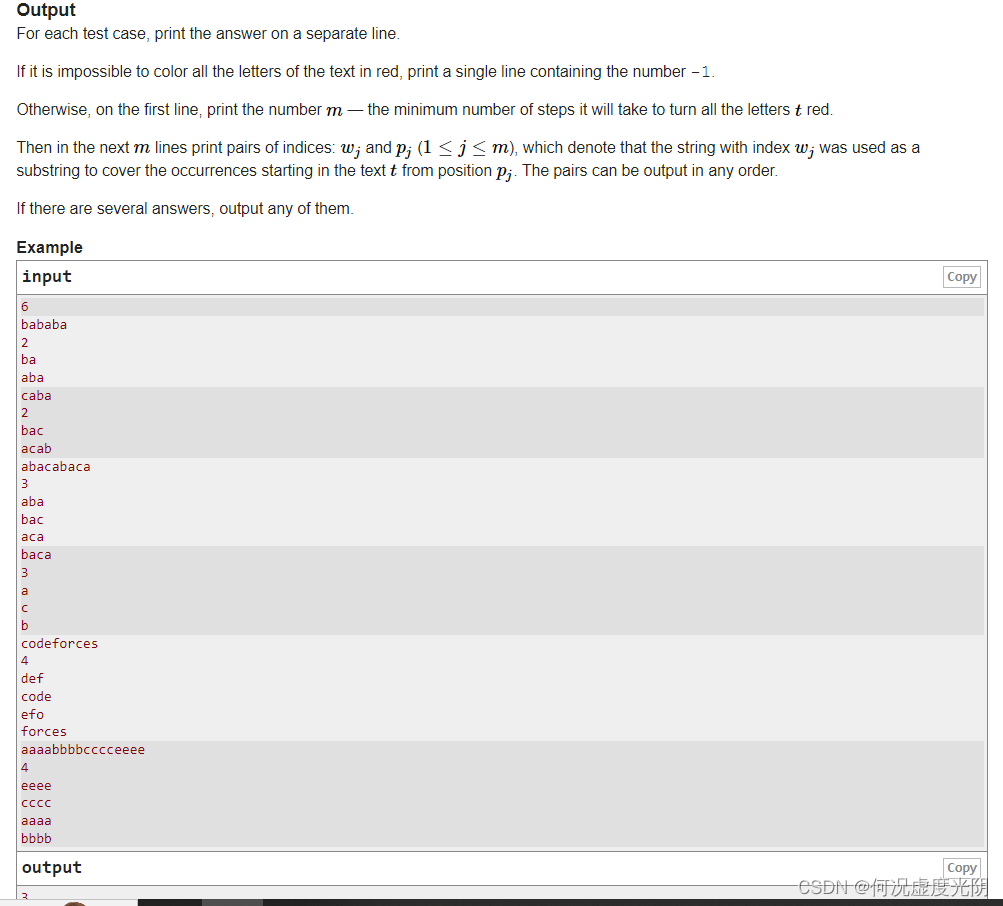
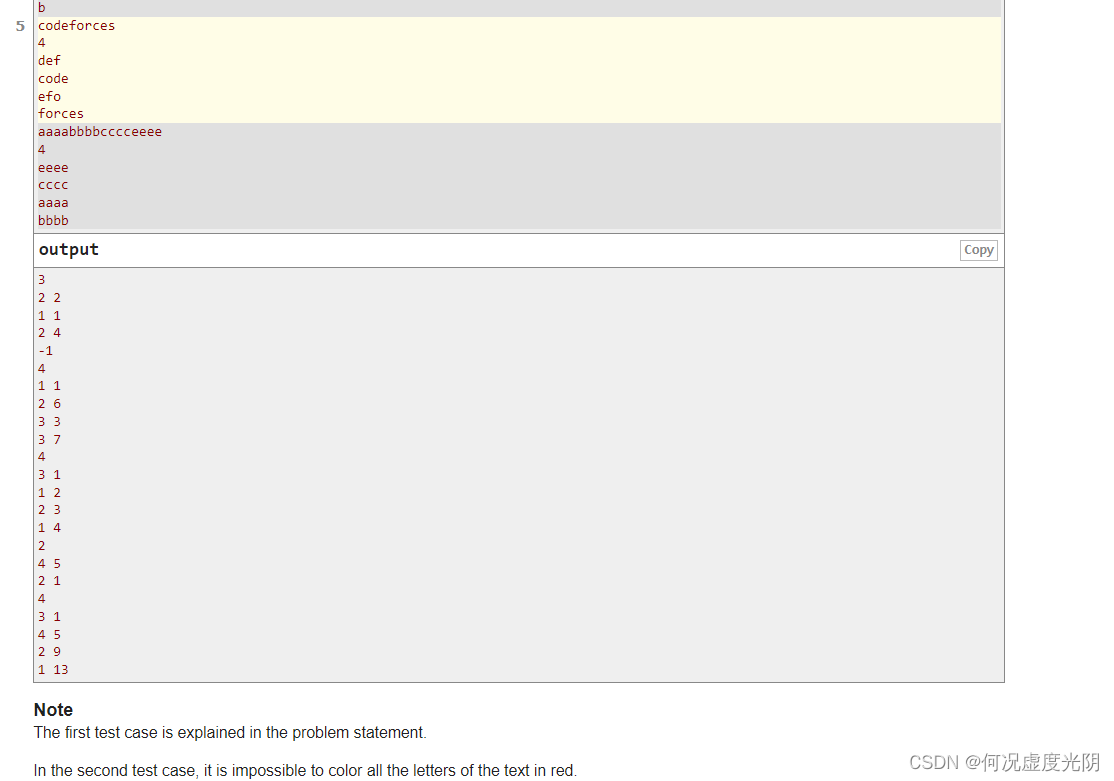
给定一个字符串 $t$ 和一组字符串 $s_1,s_2,\dots ,s_n$。每次操作可以选择其中一个字符串 $s_i$，将 $t$ 中所有 $s_i$ 的出现位置染成红色。求染成红色的最小次数以及染色方案。若无法将 $t$ 中所有字符染成红色，输出 $-1$。

思路分析

首先，我们要想到这是一道字符串的问题，需要用到字符串匹配。因为每次只能选择一个字符串染色，因此很自然的想到贪心策略。

设 $po{s}_i$ 表示染色操作中选用了第 $i$ 个字符串，$co{l}_i$ 表示染色操作中选用的 $po{s}_i$ 所染的颜色为 $i$。用 $co{l}_i[j]$ 表示在第 $j$ 次操作中，使用了第 $i$ 个字符串，从位置 $j$ 开始染色，如果没有使用第 $i$ 个字符串，则 $co{l}_i[j]$ 取 $0$。对于每个字符 $t_i$，如果 $t_i$ 没有被染色，则取 $co{l}_i[i]$ 的最大值，表示最后一次使用字符串 $i$ 时，从位置 $i$ 开始染色。

为了使染色的次数最小，需要从 $co{l}_i[i]$ 的最大值开始，往前遍历，直到最后一次出现位置，中途如果遇到已经染过色的字符，则直接跳过。在遍历的过程中，需要维护当前遍历到的位置 $j$，以及已经染色的字符的数量 $cnt$，如果 $cnt=|t|$，则表示所有字符均已染色，结束遍历。
AC代码：

#include<bits/stdc++.h>
using namespace std;
void solve(){
	string t;
	cin>>t; 
	int n;
	cin>>n;
	std::vector<std::string>s(n);
	for(int i=0;i<n;i++){
		cin>>s[i];
	} 
	int cnt=0;
	std::vector<std::array<int,2>> ans;
	while(cnt<int(t.length())){
		std::array <int,3>v{cnt,-1,-1};
		for(int i=0;i<n;i++){
			for(int j=0;j<=cnt&&j+s[i].length()<=t.length();j++){
				if(t.substr(j,s[i].length())==s[i]){
					v=max(v,array<int,3>{j+int(s[i].length()),i,j});
				}
			}
		}
		if(v[0]==cnt){
			cout<<"-1\n";
			return ;
		}
		cnt=v[0];
		ans.push_back({v[1],v[2]});
	}
	cout<<ans.size()<<"\n";
	for(auto[x,y]:ans){
		cout<<x+1<<" "<<y+1<<"\n";
	}
}
signed main(){
	int t;
	cin>>t;
	while(t--){
		solve();
	}
}