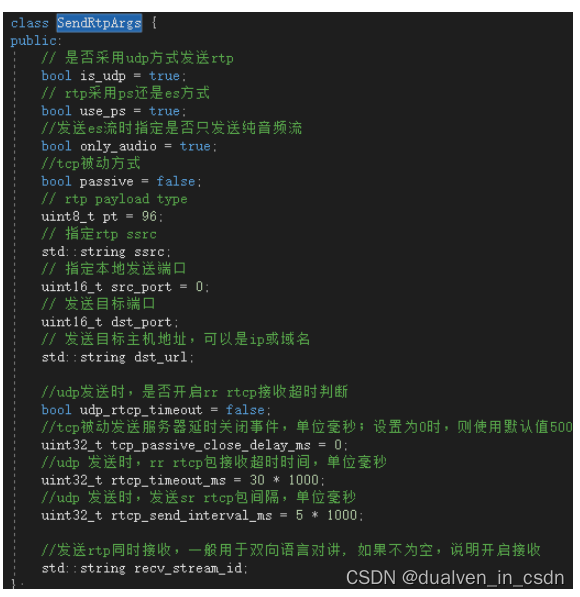
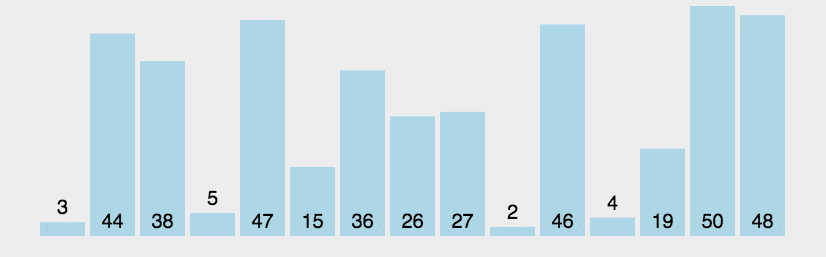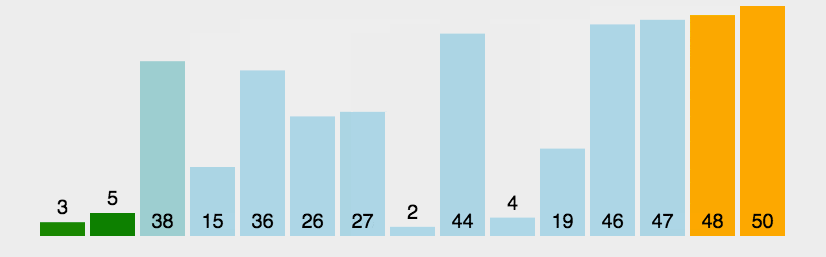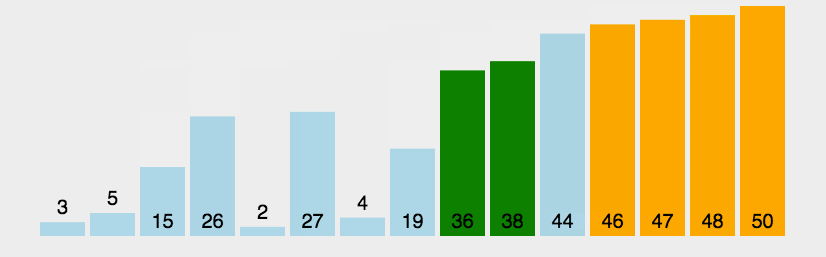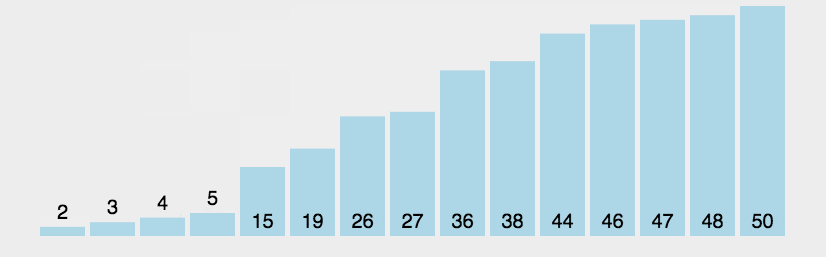1.异或的性质

🏳️🌈🏳️🌈🏳️🌈🏳️🌈🏳️🌈🏳️🌈
2.nim游戏 (基础)
891. Nim游戏 - AcWing题库
给定 n 堆石子,两位玩家轮流操作,每次操作可以从任意一堆石子中拿走任意数量的石子(可以拿完,但不能不拿),最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数 n。
第二行包含 n 个数字,其中第 i 个数字表示第 i 堆石子的数量。
输出格式
如果先手方必胜,则输出
Yes。否则,输出
No。
例如:有两堆石子,第一堆有2个,第二堆有3个,先手必胜。
操作步骤:
1. 先手从第二堆拿走1个,此时第一堆和第二堆数目相同
2. 无论后手怎么拿,先手都在另外一堆石子中取走相同数量的石子即可。
先手必败状态:a1 ^ a2 ^ a3 ^ ... ^an = 0
先手必胜状态:a1 ^ a2 ^ a3 ^ ... ^an ≠ 0
#include <iostream>
#include <cstdio>
using namespace std;
/*
先手必胜状态:先手操作完,可以走到某一个必败状态
先手必败状态:先手操作完,走不到任何一个必败状态
先手必败状态:a1 ^ a2 ^ a3 ^ ... ^an = 0
先手必胜状态:a1 ^ a2 ^ a3 ^ ... ^an ≠ 0
*/
int main(){
int n;
scanf("%d", &n);
int res = 0;
for(int i = 0; i < n; i++) {
int x;
scanf("%d", &x);
res ^= x;
}
if(res == 0) puts("No");
else puts("Yes");
}
3.nim游戏(变形)
892. 台阶-Nim游戏 - AcWing题库
现在,有一个 n 级台阶的楼梯,每级台阶上都有若干个石子,其中第 i 级台阶上有 ai 个石子(i≥1)。
两位玩家轮流操作,每次操作可以从任意一级台阶上拿若干个石子放到下一级台阶中(不能不拿)。
已经拿到地面上的石子不能再拿,最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数 n。
第二行包含 n 个整数,其中第 i 个整数表示第 i 级台阶上的石子数 ai
输出格式
如果先手方必胜,则输出
Yes。否则,输出
No。
此时我们需要将奇数台阶看做一个经典的Nim游戏,如果先手时奇数台阶上的值的异或值为0,则先手必败,反之必胜
证明:
先手时,如果奇数台阶异或非0,根据经典Nim游戏,先手总有一种方式使奇数台阶异或为0,于是先手留了奇数台阶异或为0的状态给后手
于是轮到后手:
①当后手移动偶数台阶上的石子时,先手只需将对手移动的石子继续移到下一个台阶,这样奇数台阶的石子相当于没变,于是留给后手的又是奇数台阶异或为0的状态
②当后手移动奇数台阶上的石子时,留给先手的奇数台阶异或非0,根据经典Nim游戏,先手总能找出一种方案使奇数台阶异或为0
只异或奇数的,不异或偶数的,因为最后要把石子都放到地面,地面是第0层(偶数层,如果算上地面的,也许会多一层,个人理解)
#include <iostream>
using namespace std;
int main()
{
int res = 0;
int n;
cin >> n;
for(int i = 1 ; i <= n ; i++)
{
int x;
cin >> x;
if(i % 2==1) res ^= x;//只异或奇数的
}
if(res==0) puts("No");
else puts("Yes");
return 0;
}
⭐⭐⭐代码中,先都异或了一遍,然后把
修改的位置的原来的数和修改了的数又异或了一遍
刚开始以为这不是重复了吗
其实不是,以为相同的数异或为0,0异或任何数还为原数
那么 修改的位置的原来的数异或后是0,并不影响
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5+5;
int a[N];
signed main(){
int n,q,x,y;
cin>>n>>q;
int sum = 0;
for(int i=1;i<=n;i++){
cin>>a[i];
sum^=a[i];
}
while(q--){
cin>>x>>y;
sum^=a[x];
sum^=y;
a[x] = y;
if(sum!=0){
cout<<"Kan"<<endl;
}
else{
cout<<"Li"<<endl;
}
}
return 0;
}Code over!