二叉查找树（BST）：根节点大于等于左子树所有节点，小于等于右子树所有节点。
二叉查找树中序遍历有序。

109. 有序链表转换二叉搜索树

给定一个单链表的头节点 head ，其中的元素 按升序排序 ，将其转换为高度平衡的二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差不超过 1。

示例 1:

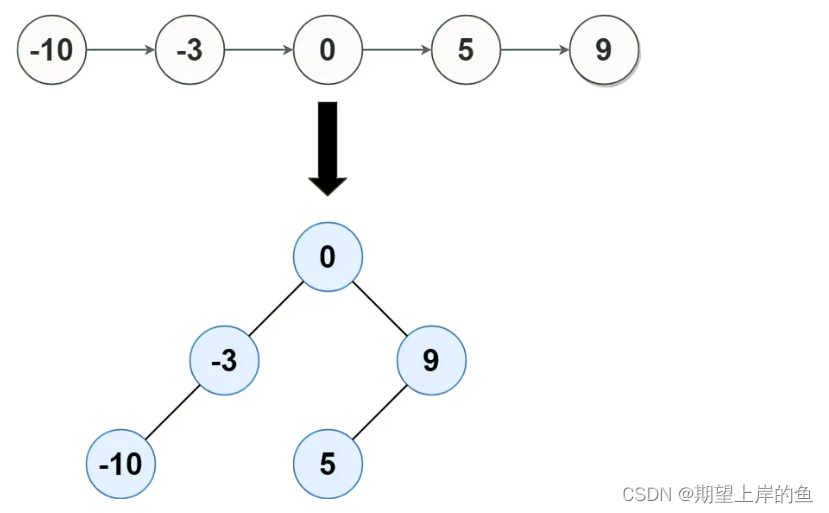
输入: head = [-10,-3,0,5,9]
输出: [0,-3,9,-10,null,5]
解释: 一个可能的答案是[0，-3,9，-10,null,5]，它表示所示的高度平衡的二叉搜索树。

示例 2:

输入: head = []
输出: []

提示:

• head 中的节点数在$[0,2\ast 10^4]$ 范围内
• $-10^5<=Node.val<=10^5$

思路：分治 + 递归

法一：
先将链表转化为数组，具体思路为：108. 将有序数组转换为二叉搜索树

法二：快慢指针

和法一类似，我们使用快慢指针要找到有序链表的中位数，以该中位数为根节点，并将该中位数左右两边分成两个子有序链表，再在子有序链表找中位数，以此类推递归。

代码：(Java、C++)

法一：
Java

class Solution {
    public TreeNode sortedListToBST(ListNode head) {
        List<Integer> nums = new ArrayList<>();
        while(head != null){
            nums.add(head.val);
            head = head.next;
        }
        TreeNode root = toBST(nums, 0, nums.size() - 1);
        return root;
    }
    public TreeNode toBST(List<Integer> nums, int be, int ed){
        if(be > ed) return null;
        TreeNode root = new TreeNode(nums.get(be + (ed - be) / 2));
        root.left = toBST(nums, be, be + (ed - be) / 2 - 1);
        root.right = toBST(nums, be + (ed - be) / 2 + 1, ed);
        return root;
    }
}

C++

class Solution {
public:
    TreeNode* sortedListToBST(ListNode* head) {
        vector<int> nums;
        while(head != nullptr){
            nums.push_back(head->val);
            head = head->next;
        }
        TreeNode* root = toBST(nums, 0, nums.size() - 1);
        return root;
    }
    TreeNode* toBST(vector<int>& nums, int be, int ed){
        if(be > ed) return nullptr;
        TreeNode* root = new TreeNode(nums[be + (ed - be) / 2]);
        root->left = toBST(nums, be, be + (ed - be) / 2 - 1);
        root->right = toBST(nums, be + (ed - be) / 2 + 1, ed);
        return root;
    }
};

法二：快慢指针
Java

class Solution {
    public TreeNode sortedListToBST(ListNode head) {
        if(head == null) return null;
        if(head.next == null) return new TreeNode(head.val);
        ListNode preMid = getPreMid(head);
        TreeNode root = new TreeNode(preMid.next.val);
        root.right = sortedListToBST(preMid.next.next);
        preMid.next = null;
        root.left = sortedListToBST(head);
        return root;
    }
    public ListNode getPreMid(ListNode head){
        ListNode slow = head;
        ListNode pre = head;
        ListNode fast = head;
        while(fast != null && fast.next != null){
            pre = slow;
            slow = slow.next;
            fast = fast.next.next;
        }
        return pre;
    }
}

C++

class Solution {
public:
    TreeNode* sortedListToBST(ListNode* head) {
        if(head == nullptr) return nullptr;
        if(head->next == nullptr) return new TreeNode(head->val);
        ListNode* preMid = getPreMid(head);
        TreeNode* root = new TreeNode(preMid->next->val);
        root->right = sortedListToBST(preMid->next->next);
        preMid->next = nullptr;
        root->left = sortedListToBST(head);
        return root;
    }
    ListNode* getPreMid(ListNode* head){
        ListNode* slow = head;
        ListNode* pre = head;
        ListNode* fast = head;
        while(fast != nullptr && fast->next != nullptr){
            pre = slow;
            slow = slow->next;
            fast = fast->next->next;
        }
        return pre;
    }
};

运行结果：

复杂度分析：

• 时间复杂度：$O(n)$，其中 n 是链表的长度。
• 空间复杂度：$O(logn)$，法一为$O(n)$，需要长度为n的数组；法二为$O(n)$，这里只计算除了返回答案之外的空间。平衡二叉树的高度为 $O(logn)$，即为递归过程中栈的最大深度，也就是需要的空间。

题目来源：力扣。

放弃一件事很容易，每天能坚持一件事一定很酷，一起每日一题吧！
关注我 leetCode专栏，每日更新！

注： 如有不足，欢迎指正！