基于格密码的LWE问题

LWE

LWE问题， Learning With Errors，带有安全性证明的第一个版本是由Oded Regev 在2005年提出，Kawachi等给出了效率的改进，接着一些效率方面非常重要的改进由Peikert等提出。

格理论知识

格密码学（Lattice-based Crypto）是现在比较火的一个密码学分支，而且本身拥有抵抗量子计算（最近几年征集的抗量子计算的密码大致有基于HASH函数的密码、基于纠错码的密码、基于格的密码、多变量二次方程组密码、秘密钥密码）的特性。

整数格：设 $v_1,\cdots,v_n \in \mathbb{R}^m$ 为一组线性无关的向量。由 $v_1,\cdots,v_n$ 生成的格 $L$ 指的是向量 $v_1,\cdots,v_n$ 的线性组合构成的向量集合，且其所使用的系数均在 $\mathbb{Z}$ 中，即 $\{a_1v_1+a_2v_2+\cdots+a_nv_n:a_1,a_2,\cdots,a_n\in\mathbb{Z}\}$

格 $L$ 的维数等于格中向量的个数。

假定 $v_1,v_2,\cdots,v_n$ 是格 $L$ 的基， $w_1,w_2,\cdots,w_n \in L$ ，则必然存在整系数 $a_{ij}$ 使得：

$\begin{cases} w_1=a_{11}v_1+a_{12}v_2+\cdots+a_{1n}v_n \\ w_2=a_{21}v_1+a_{22}v_2+\cdots+a_{2n}v_n \\ \vdots \\ w_n=a_{n1}v_1+a_{n2}v_2+\cdots+a_{nn}v_n \end{cases}$

这样，格的问题就是矩阵运算了。

难解问题

最短向量问题（SVP，The Shortest Vector Problem）：

寻找一个格 $L$ 中最短的非零向量。即，寻找一个 $\in L$ 满足其欧几里德范数 $\mid\mid v \mid\mid$ 最小。

最接近向量问题（CVP，The Closest Vector Problem）：

对于一个非格 $L$ 中的向量 $w$ ，在格中寻找一个向量 $v$ ，使得 $\mid\mid w-v \mid\mid$ 最小。

CVP和SVP都是NP完备问题，因此求解起来十分困难，因此这两个问题都是可以作为密钥体制基础的。

LWE相关数学基础

LWE是一个CVP问题

在这里插入图片描述

LWE有搜索LWE（SLWE）和决策LWE（DLWE），SLWE最后的问题是需要我们找到s，而DLWE只需要让我们辨别看到的到底是LWE问题中的误差乘积还是一个随机生成的向量。

基于LWE的公钥密码体制

参数：n、m、l、t、r、q和一个实数 $\alpha$ ( $\alpha>0$ )

私钥：均匀随机的选取 $\in \mathbb{Z}^{n*l}_q$

公钥：均匀随机的选取 $\in \mathbb{Z}^{m*n}_q$ 和 $\in \mathbb{Z}^{m*l}_q$ 。公钥是 $（A，P=AS+E）\in \mathbb{Z}^{m*n}_q* \mathbb{Z}^{m*l}_q$

加密：给定原文空间中一个元素 $\in \mathbb{Z}^l_t$ ，和一个公钥(A,P)，均匀随机选取一个向量 $\in \{-r,-r+1,…,r\}^m$ ，然后输出一个密文（ $U = A^T*a,c = P^T*a+f(v)$ ） $\in \mathbb{Z}^n_q* \mathbb{Z}^l_q$

解密：给定一个密文 $(u,c)\in \mathbb{Z}^n_q* \mathbb{Z}^l_q$ 和一个私钥 $\in \mathbb{Z}^{n*l}_q$ ，输出 $f^{-1}(c-s^Tu)$

这个密码体制中存在某个正的解密错误概率，这个概率可以通过选取适当的参数使得它变得很小。此外，在加密前如果一个纠错码被用来对一个信息进行编码，则错误概率可以被减少到不被发现的水平。（关于解密错误发生的概率评估详见《抗量子计算密码》）

ctf中出现的

随机选取一个矩阵 $\in \mathbb{Z}^{m*n}_q$ ，一个随机向量 $\in \mathbb{Z}^n_q$ ，和一个随机的噪音 $\in \varepsilon^m$

一个LWE系统的输出 $g_A(s,e) = As+e\mod q$

一个LWE问题是，给定一个矩阵A，和LWE系统的输出 $g_A(s,e)$ ，还原s

（LWE的误差向量是一个满足正态分布的小向量）

因为加入了一些误差，如果使用高斯消元法的话，这些误差会聚集起来，使得解出来的东西跟实际值差很多。

求解

构造矩阵：
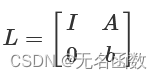
在这里插入图片描述

利用LLL算法和Babai最近平面算法，可以在多项式时间内找到SVP近似解。

利用Embedding Technique构造一个Embedding Lattice，也可以解SVP。

LLL算法

高斯提出了如果在二维格中找到一组优质基的算法，这个算法的基本思想是从一个基向量中交替减去另一个基向量的倍数，直到没有更好的改进为止。（所谓没有更好的改进就是要满足算法中一个特定的条件要求）：

高斯格基约减算法

输入：格L的一组基 $v_1$ 和 $v_2$

输出：一组具有良好正交性的基向量

循环
如果 $\parallel v_2\parallel<\parallel v_1\parallel$ ，交换 $v_1和v_2$
计算 $\left\lceil\frac{v_1*v_2}{\parallel v1\parallel^2}\right\rfloor$ (计算施密特正交化的系数)
如果m = 0,返回基向量 $v_1$ 和 $v_2$
用 $v_2 - mv_1$ 替换 $v_2$
继续循环

更准确的说，当这个算法终止的时候，向量 $v_1$ 就是格L中最短的非零向量，因此说这个算法可以很好的解决SVP问题

sagemath代码

def Gauss(x,y):
    # step 1
    v1 = x; v2 = y
    finished = False
    # step 2
    while not finished:
        # (a)
        m = round(( v2.dot_product(v1) / v1.dot_product(v1) ))
        # (b)
        v2 = v2 - m*v1
        # (c)
        if v1.norm() <= v2.norm():
            finished = True
        else:
            v1, v2 = v2, v1
    
   return v1, v2

LLL算法

1982年诞生的LLL算法可视为高斯算法在高维格中的推广

该算法可以解决某些维数较低的格中的SVP和CVP问题。但随着格的维数的增高，该算法的运行效果也随之减弱，以至于对于高维格来说，即使应用LLL算法，也无法很好的解决SVP和CVP问题。所以大多数基于格理论的密码系统的安全性，都依赖LLL算法以及其他格基约减算法能否高效解决apprSVP(近似最短向量问题)或apprCVP(近似最接近向量问题)问题的困难性。

用LLL约化基需要这组基满足两个条件：

1.size-reduce：对于所有的 $1 \leq j < i \leq n$ ，有 $|\mu_{i,j}| \le \frac{1}{2}$ ， $\mu_{i,j}=\frac{|v_i*v_j^*|}{||v_j^*||}$ 为施密特正交化中的系数。

2.Lovász condition：对于所有的 $1 < i \leq n$ ， $||v_i^*||^2\ge(\frac{3}{4}-\mu^2_{i,i-1})||v_{i-1}^*||^2$ 成立

sagemath代码简单实现：

def max(a, b):
    return a if a > b else b

def LLL_v0(M, delta=0.75):
    B = deepcopy(M)
    Q, mu = B.gram_schmidt()
    n, k = B.nrows(), 1
    
    while k < n:
        
        # size reduction step
        for j in reversed(range(k)):
            if abs( mu[k][j] ) > 0.5:
                B[k] = B[k] - round( mu[k][j] ) * B[j]
                Q, mu = B.gram_schmidt()
        
        # swap step 
        if Q[k].dot_product(Q[k]) >= (delta - mu[k][k-1]^2) * Q[k-1].dot_product(Q[k-1]):
            k = k + 1
        else:
            B[k], B[k-1] = B[k-1], B[k]
            Q, mu = B.gram_schmidt()
            k = max(k-1,1)
    
    return B

常规实现

在进行一次交换步或约化步之后，实际上只需要修改 $\mu$ （施密特正交化系数）和Q（正交向量组）的个别值。而简易实现中，每次都会重新计算整个施密特正交化，这样的实现是低效的。

def LLL_v1(M, delta=0.75):

    if delta < 0.25:
        print("delta should be greater than 0.25. Choose delta = 0.75 now.")
    alpha = delta if 0.25 < delta < 1 else 0.75
    
    x = M
    n = M.nrows()
    
    def reduce(k, l):
        do_reduce = False
                   
        if abs(mu[k,l]) > 0.5:
            do_reduce = True
            
            y[k] = y[k] - mu[k,l].round() * y[l]
            for j in range(l):
                mu[k,j] -=  mu[k,l].round() * mu[l,j]
            mu[k,l] = mu[k,l] - mu[k,l].round()       

        return
    
    def exchange(k):
        
        y[k-1], y[k] = y[k], y[k-1]
        NU = mu[k,k-1]
        delta = gamma[k] + NU ^ 2 * gamma[k-1]
        mu[k,k-1] = NU * gamma[k-1] / delta    # all above is right
        gamma[k] = gamma[k] * gamma[k-1] / delta
        gamma[k-1] = delta

        for j in range(k-1):
            mu[k-1,j], mu[k,j] = mu[k,j], mu[k-1,j]
        for i in range(k+1, n):
            xi = mu[i,k]
            mu[i,k] = mu[i,k-1] - NU * mu[i,k]
            mu[i,k-1] = mu[k,k-1] * mu[i,k] + xi      
            
        return
    
    # step (1) 
    y = deepcopy(x)
    # step (2) 
    y_star, mu = y.gram_schmidt()
    gamma = [y_star[i].norm() ^ 2 for i in range(n)]
    
    # step (3)
    k = 1
    
    # step (4)
    while k < n:      
        # step (4)(a)    
        reduce(k, k-1)

        # step (4)(b)
        if gamma[k] >= (alpha - mu[k,k-1]^2) * gamma[k-1]:
            # (i)
            for l in reversed(range(k-1)):
                reduce(k, l)
            # (ii)
            k = k + 1
        else:
            # (iii)
            exchange(k)
            # (iv)
            if k > 1:
                k = k-1

    return y

Babai最近平面算法

该算法主要由两步。第一步针对输入的格，输出LLL约化基；此时针对此约化基向量，形成整数线性组合，来保证与给定的向量t足够近。这个步骤跟LLL算法的内循环约化操作很类似

def BabaisClosestPlaneAlgorithm(L, w):
    '''
    Yet another method to solve apprCVP, using a given good basis.
    INPUT:
    * "L" -- a matrix representing the LLL-reduced basis (v1, ..., vn) of a lattice.
    * "w" -- a target vector to approach to.
    OUTPUT:
    * "v" -- a approximate closest vector.
    Quoted from "An Introduction to Mathematical Cryptography":
    In both theory and practice, Babai's closest plane algorithm
    seems to yield better results than Babai's closest vertex algorithm.
    '''
    G, _ = L.gram_schmidt()
    t = w
    i = L.nrows() - 1
    while i >= 0:
        w -= round( (w*G[i]) / G[i].norm()^2 ) * L[i]
        i -= 1
    return t - w

Embedding Technique

（不会用软件画图所有写纸上了，回头整理却找不到博客了，凑合看吧）

在这里插入图片描述

解题代码

例1：2020祥云杯 Easy Matrix

import numpy as np
from secret import *

def random_offset(size):
    x = np.random.normal(0, 4.7873, size)
    return np.rint(x)

secret = np.array(list(flag))

column = len(list(secret))
row = 128
prime = 2129

matrix = np.random.randint(512, size=(row, column))
product = matrix.dot(secret) % prime
offset = random_offset(size=row).astype(np.int64)
result = (product + offset) % prime

np.save("matrix.npy", matrix)
np.save("result.npy", result)

利用LLL算法和Babai最近平面算法

import numpy as np
from sage.modules.free_module_integer import IntegerLattice

def BabaisClosestPlaneAlgorithm(L, w):
    G, _ = L.gram_schmidt()
    t = w
    i = L.nrows() - 1
    while i >= 0:
        w -= round( (w*G[i]) / G[i].norm()^2 ) * L[i]
        i -= 1
    return t - w

row = 128
col = 42
p = 2129

M = Matrix(list(np.load('matrix.npy')))
R = vector(list(np.load('result.npy')))

A = [[0 for _ in range(row)] for _ in range(row)]
for i in range(128):
    for j in range(128):
        if i==j:
            A[i][j] = p
A = Matrix(A)
L = Matrix(A.stack(M.transpose()))
lattice = IntegerLattice(L, lll_reduce=True)
closest_vector = BabaisClosestPlaneAlgorithm(lattice.reduced_basis, R)

FLAG = Matrix(Zmod(p), M)
flag = FLAG.solve_right(closest_vector)
print(''.join( chr(i) for i in flag))

例2：利用Embedding Technique构造一个Embedding Lattice的代码

# Sage
DEBUG = False
m = 44
n = 55
p = 2^5
q = 2^10

def errorV():
  return vector(ZZ, [1 - randrange(3) for _ in range(n)])

def vecM():
  return vector(ZZ, [p//2 - randrange(p) for _ in range(m)])

def vecN():
  return vector(ZZ, [p//2 - randrange(p) for _ in range(n)])

def matrixMn():
  mt = matrix(ZZ, [[q//2 - randrange(q) for _ in range(n)] for _ in range(m)])
  return mt

A = matrixMn()
e = errorV()
x = vecM()
b = x*A+e

if DEBUG:
  print('A = \n%s' % A)
  print('x = %s' % x)
  print('b = %s' % b)
print('e = %s' % e)

z = matrix(ZZ, [0 for _ in range(m)]).transpose()
beta = matrix(ZZ, [1])
T = block_matrix([[A, z], [matrix(b), beta]])
if DEBUG:
  print('T = \n%s' % T)

print('-----')
L = T.LLL()
print(L[0])
print(L[0][:n] == e)