引言
本篇是最近有遇到过的一个题目,关于二叉树的遍历,正好有一些经验与技巧,所以开一篇帖子记录一下。
二叉树遍历介绍
遍历是数据结构中常见的操作,主要是将所有元素都访问一遍。对于线性结构来说,遍历分为两种:正序遍历和逆序遍历。而对于树形结构来说,根据节点访问顺序不同,二叉树的遍历分为如下4种:
- 前序遍历(Preorder Traversal)
- 中序遍历(Inorder Traversal)
- 后序遍历(Postorder Traversal)
- 层序遍历(Levelorder Traversal)
二叉树的数据结构为:
struct Node
{
Node* left;
Node* right;
int data;
};
二叉树前序遍历
一般先序遍历的顺序为,根、左子节点、右子节点→根(左子节点)、左叶子节点、右叶子结点→ 根(右子节点)、左叶子结点、右叶子结点(PS:这里顺序是三层,下面的都是,但图是4层)。即先根再左最后右,简称根左右,具体如下图所示:

那么我们可以写出它的递归形式代码:
void preorderTraversal(Node* p)
{
if (!p) return;
cout << p->data << " ";
preorderTraversal(p->left);
preorderTraversal(p->right);
}
二叉树中序遍历
中序遍历的顺序为左叶子结点、根(左子节点)、右叶子结点 → 左子节点、根、左叶子结点 → 左叶子节点、根(右子节点)、右叶子结点,即先左再根最后右,简称左根右,示意图为:

同样写出递归形式代码:
void inorderTraversal(Node* p)
{
if (!p) return;
inorderTraversal(p->left);
cout << p->data << " ";
inorderTraversal(p->right);
}
二叉树后序遍历
中序遍历的顺序为左叶子结点、右叶子结点、根(左子节点) → 左叶子节点、右叶子结点、根(右子节点) → 左子节点、左子结点、根,即先左再右最后根,简称左右根,示意图为:

那么它的递归形式代码为:
void postorderTraversal(Node* p)
{
if (!p) return;
postorderTraversal(p->left);
postorderTraversal(p->right);
cout << p->data << " ";
}
二叉树层序遍历
还有一种层序遍历,这种就字面意思,从上到下,从左至右,直接给出示意图为:

那么代码为:
void levelOrderTraversal(Node* root)
{
queue<Node*> q;
q.push(root);
while (!q.empty())
{
Node* p = q.front(); q.pop();
cout << p->data << " ";
if (p->left) q.push(p->left);
if (p->right) q.push(p->right);
}
}
该函数使用队列来跟踪需要访问的节点,它首先将根节点推送到队列中,然后,它进入一个循环,该循环一直持续到队列为空。在循环的每次迭代中,它都会将前面的节点p从队列中移出,打印其数据,并将其左右子节点推到队列中,这样就达到了层级的效果。
二叉树遍历全代码
这里因为上面定义的结构体没有分成两部分,仅仅只定义了单节点,没有考虑多关系问题,不过反而代码思路会更加清晰,除了定义测试用例会复杂些,这里我们建立二元树结构:
Node* root = new Node{
new Node{ new Node{ nullptr, nullptr, 4 }, new Node{ nullptr, nullptr, 5 }, 2 },
new Node{ new Node{ nullptr, nullptr, 6 }, new Node{ nullptr, nullptr, 7 }, 3 },
1
};
我最近正好在学cpp,nullptr在c语言里就是NULL,空指针。将其展开为如下形式:
1
/ \
/ \
/ \
2 3
/ \ / \
4 5 6 7
该种形式当然可以更改结构体构造方式,比如二叉树的四种遍历方式中提到的:
struct treenode {
int val;
treenode *left;
treenode *right;
treenode() : val(0), left(nullptr), right(nullptr) {}
treenode(int x) : val(x), left(nullptr), right(nullptr) {}
treenode(int x, treenode *left, treenode *right) : val(x), left(left), right(right) {}
};
不过这里还是以自定义二元树结构来产生初值,那么将上述代码汇总为:
#include <iostream>
#include <queue>
#include <stack>
using namespace std;
struct Node
{
Node* left;
Node* right;
int data;
};
// preorder traversal
void preorderTraversal(Node* p)
{
if (!p) return;
cout << p->data << " "; // 先输出根
preorderTraversal(p->left); // 次输出左子树
preorderTraversal(p->right);// 最后右子树
}
// inorder traversal
void inorderTraversal(Node* p)
{
if (!p) return;
inorderTraversal(p->left);
cout << p->data << " ";
inorderTraversal(p->right);
}
// postorder traversal
void postorderTraversal(Node* p)
{
if (!p) return;
postorderTraversal(p->left);
postorderTraversal(p->right);
cout << p->data << " ";
}
// level-order traversal
void levelOrderTraversal(Node* root)
{
queue<Node*> q;
q.push(root);
while (!q.empty())
{
Node* p = q.front(); q.pop();
cout << p->data << " ";
if (p->left) q.push(p->left);
if (p->right) q.push(p->right);
}
}
int main()
{
// create binary tree
Node* root = new Node{
new Node{ new Node{ nullptr, nullptr, 4 }, new Node{ nullptr, nullptr, 5 }, 2 },
new Node{ new Node{ nullptr, nullptr, 6 }, new Node{ nullptr, nullptr, 7 }, 3 },
1
};
// perform traversals
cout << "Preorder traversal: ";
preorderTraversal(root);
cout << endl;
cout << "Inorder traversal: ";
inorderTraversal(root);
cout << endl;
cout << "Postorder traversal: ";
postorderTraversal(root);
cout << endl;
cout << "Level-order traversal: ";
levelOrderTraversal(root);
cout << endl;
return 0;
}
进行编译后,打印输出:
Preorder traversal: 1 2 4 5 3 6 7
Inorder traversal: 4 2 5 1 6 3 7
Postorder traversal: 4 5 2 6 7 3 1
Level-order traversal: 1 2 3 4 5 6 7
手算遍历的一些技巧
一般如果从选择题的角度,需要给出前中,或者中后,来确定二叉树形态,再推中序遍历,即:
前序、中序——> 后序
后序、中序——> 前序
如果给了前后序的话,那么问题就变为了求多少种二叉树结构,比如说2011年的统考题:
【2011统考真题】一棵二叉树的前序遍历序列和后序遍历序列分别为1,2,3,4和4,3,2,1,该二叉树的中序遍历序列不会是( ).
A . A. A.:1、2、3、4
B . B. B.:2、3、4、1
C . C. C.:3、2、4、1
D . D. D.:4、3、2、1
该题就是因为前序NLR与后序LRN序列刚好相反,所以无法确定一颗完整的二叉树,但可以确定二叉树中结点的祖先关系。根据这就能大致推断出中序结点顺序,比如说这里的仅考虑以1为孩子的结点2为根结点的子树,它也只能有左孩子。
所以这里仅考虑在有中序的前提下,推另一种的情况下,整个过程可以表示成如下图:
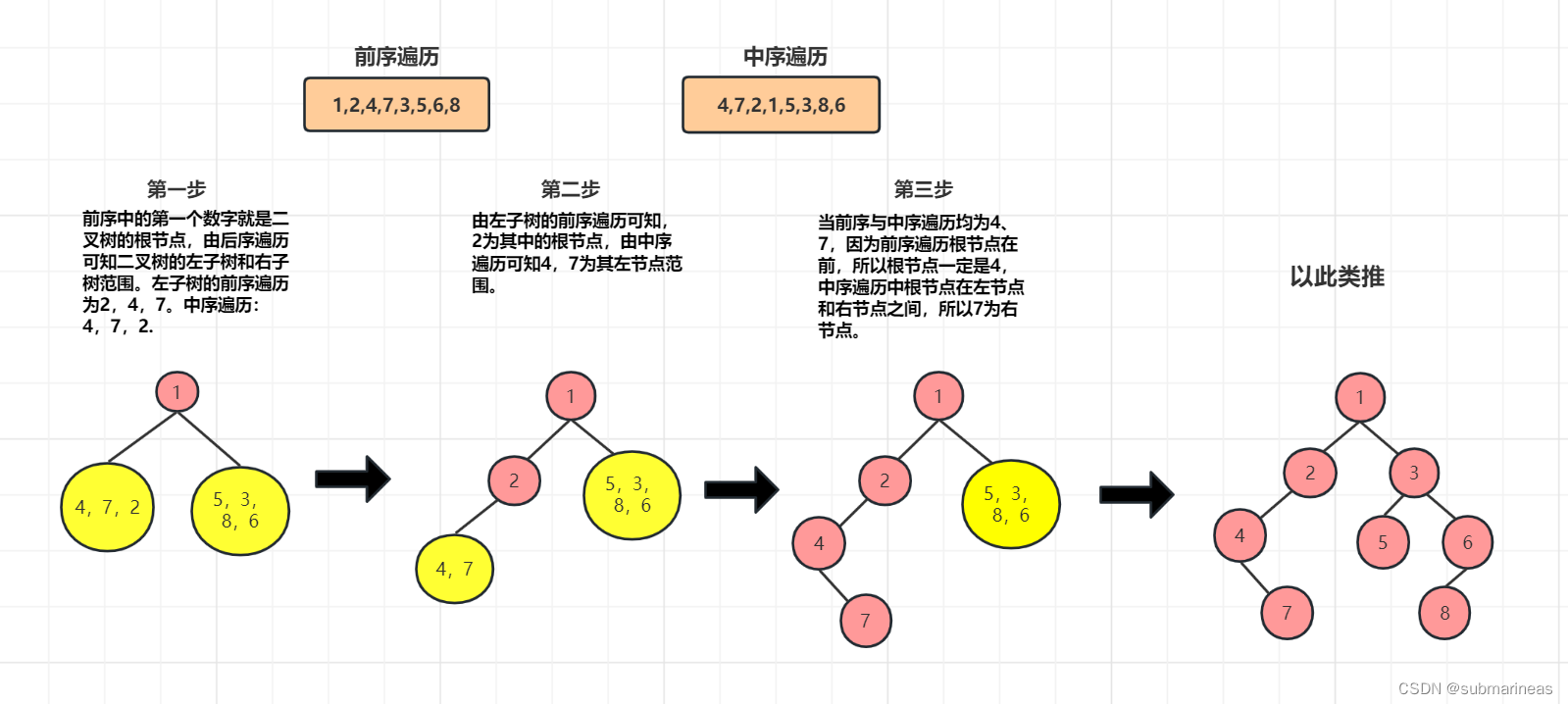
这是比较官方的做法,根节点给的也很明显,能够快速定位并进一步分治,另一种就是依据超级简单-投影法遍历树,引用其中的一种遍历方式如下:
后序遍历就像在右边大风的情况下,将二叉树树枝刮向左方,且顺序为左子树、右子树、根,太阳直射,将所有的结点投影到地上。图中的二叉树,其后序序列投影如图所示。后序遍历序列为:DEBGFCA。
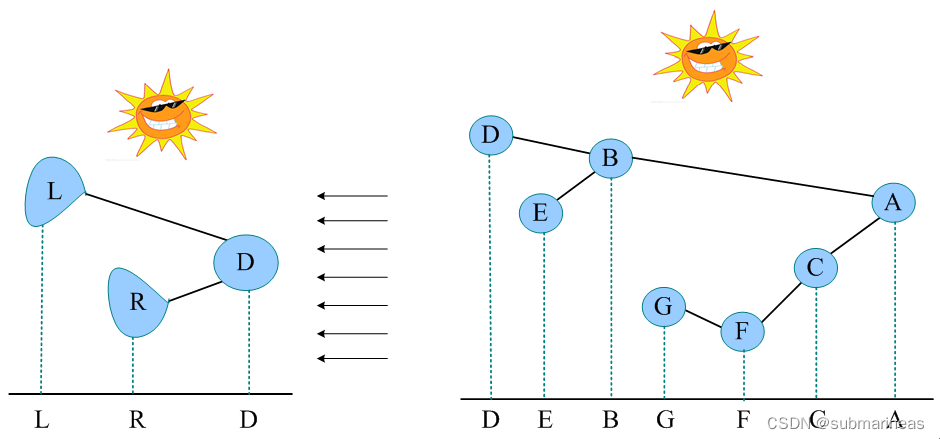
但该种方式其实只考虑了一维向量,或者说把横线看成是一根坐标轴,仅仅考虑了x的方向变化,而下面这种方法,是通过横轴与竖轴一起确立的唯一二叉树,这里先略过规则,直接看我画的如下图:
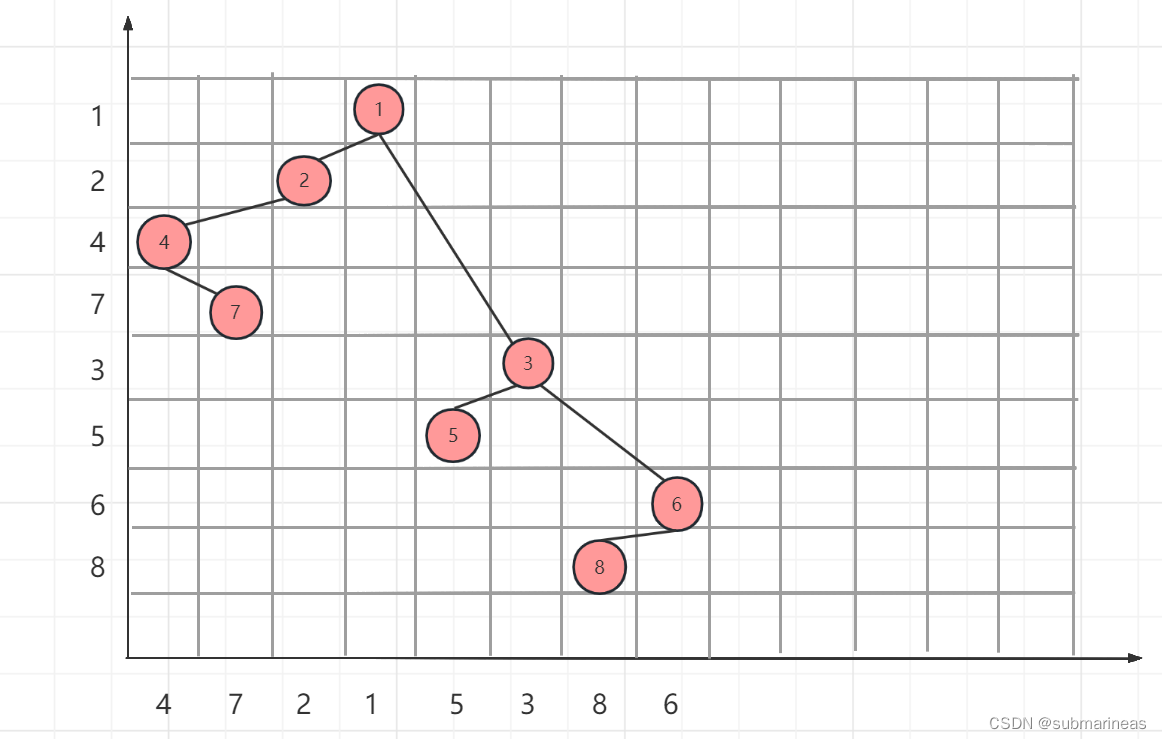
(PS:画了坐标轴,反而比不画的时候丑了很多,emmm,得学学怎么作图)
该方案,源自B站的无脑秒解!已知先/后序遍历与中序遍历,求后/先序遍历。我们发现将中序遍历的输出放y轴上,前序和后序放x轴上,然后点对点将它连起来后,结果与正常做法没有什么两样,这里还可以用我之前在数据结构设计题大题总结(非代码) 该篇中引用的一张百度百科图同样适用:
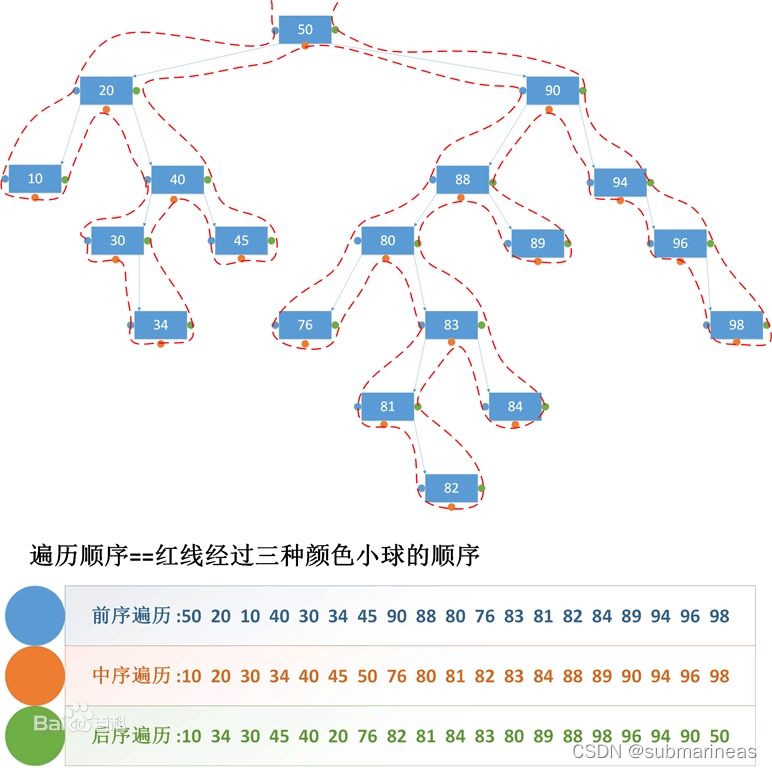
当然,我算的是另一个,这个20个序列太多了,我在iPad上画的稍微简单点,能一页表达完整的题:

关于这种求解的证明也很简单,因为先序是根左右,中序是左根右,所以:

而已知后序(左右根),颠倒后变为(根右左),则同样是上图。
二叉树遍历coding
这里其实也是两题:
从前序与中序遍历序列构造二叉树
从中序与后序遍历序列构造二叉树
这里以前序和中序题为例,题目为:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
这里找了一个动态图演示:

解题思路就是我前面所提到的加上一点小细节:
在中序遍历中对根节点进行定位时,一种简单的方法是直接扫描整个中序遍历的结果并找出根节点,但这样做的时间复杂度较高。我们可以考虑使用哈希表来帮助我们快速地定位根节点。对于哈希映射中的每个键值对,键表示一个元素(节点的值),值表示其在中序遍历中的出现位置。在构造二叉树的过程之前,我们可以对中序遍历的列表进行一遍扫描,就可以构造出这个哈希映射。在此后构造二叉树的过程中,我们就只需要 O(1)O(1) 的时间对根节点进行定位了。
所以代码为:
class Solution {
private:
unordered_map<int, int> index;
public:
TreeNode* myBuildTree(const vector<int>& preorder, const vector<int>& inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
if (preorder_left > preorder_right) {
return nullptr;
}
// 前序遍历中的第一个节点就是根节点
int preorder_root = preorder_left;
// 在中序遍历中定位根节点
int inorder_root = index[preorder[preorder_root]];
// 先把根节点建立出来
TreeNode* root = new TreeNode(preorder[preorder_root]);
// 得到左子树中的节点数目
int size_left_subtree = inorder_root - inorder_left;
// 递归地构造左子树,并连接到根节点
// 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
root->left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
// 递归地构造右子树,并连接到根节点
// 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
root->right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int n = preorder.size();
// 构造哈希映射,帮助我们快速定位根节点
for (int i = 0; i < n; ++i) {
index[inorder[i]] = i;
}
return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
}
};
后序和中序定位也一样,后序的尾结点为根节点,另外,同样可以构造哈希映射,帮助我们快速定位根节点:
class Solution {
int post_idx;
unordered_map<int, int> idx_map;
public:
TreeNode* helper(int in_left, int in_right, vector<int>& inorder, vector<int>& postorder){
// 如果这里没有节点构造二叉树了,就结束
if (in_left > in_right) {
return nullptr;
}
// 选择 post_idx 位置的元素作为当前子树根节点
int root_val = postorder[post_idx];
TreeNode* root = new TreeNode(root_val);
// 根据 root 所在位置分成左右两棵子树
int index = idx_map[root_val];
// 下标减一
post_idx--;
// 构造右子树
root->right = helper(index + 1, in_right, inorder, postorder);
// 构造左子树
root->left = helper(in_left, index - 1, inorder, postorder);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
// 从后序遍历的最后一个元素开始
post_idx = (int)postorder.size() - 1;
// 建立(元素,下标)键值对的哈希表
int idx = 0;
for (auto& val : inorder) {
idx_map[val] = idx++;
}
return helper(0, (int)inorder.size() - 1, inorder, postorder);
}
};