🎇C++笔试强训
- 博客主页:一起去看日落吗
- 分享博主的C++刷题日常,大家一起学习
博主的能力有限,出现错误希望大家不吝赐教- 分享给大家一句我很喜欢的话:夜色难免微凉,前方必有曙光 🌞。
💦🔥
选择题
💦第一题
对于顺序存储的线性表,访问结点和增加结点的时间复杂度为()。
A O(n) O(n)
B O(n) O(1)
C O(1) O(n)
D O(1) O(1)
线性表可以直接通过下标访问,和元素的多少没有关系,所以访问时间复杂度为O1
增加结点需要看节点个数,所以是On
这道题的答案是C
💦第二题
在下列链表中不能从当前结点出发访问到其余各结点的是()
A 双向链表
B 单循环链表
C 单链表
D 双向循环链表
单链表只可以往后走,如果指针从中间开始,则不能访问前面的节点
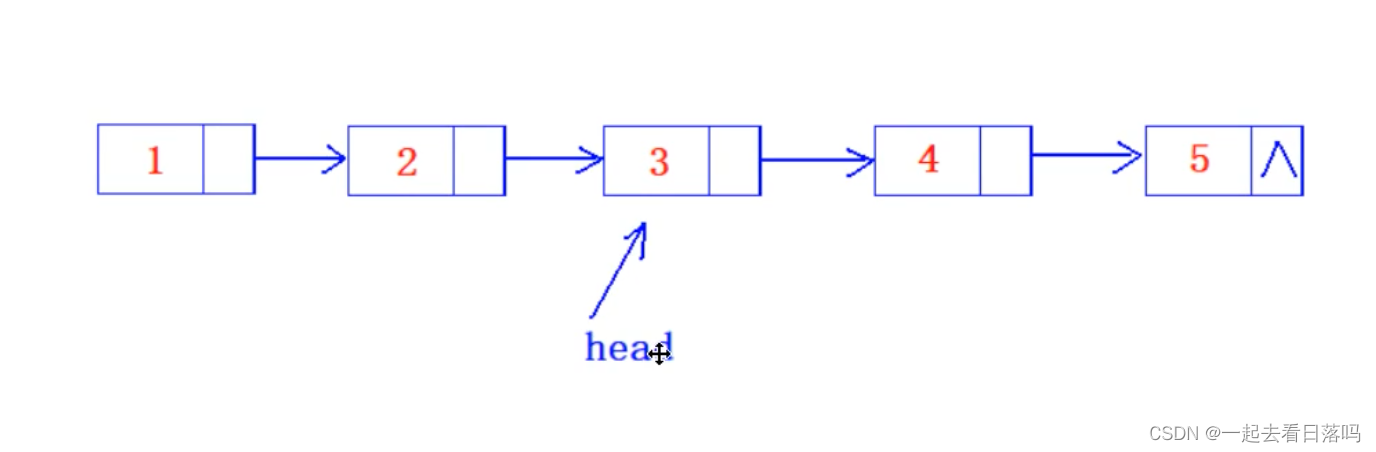
这道题的答案是C
💦第三题
完成在双向循环链表结点 p 之后插入 s 的操作是()
A p->next=s;s->prior=p;p->next->prior=s;s->next=p->next
B p->next->prior=s;p->next=s;s->prior=p;s->next=p->next
C s->prior=p;s->next=p->next;p->next=s;p->next->prior=s
D s->prior=p;s->next=p->next;p->next->prior=s;p->next=s
数据结构画图是关键
修改指针的时候,需要先把插入节点的前后连起来
每个人的插入顺序可能不一样,所以我们可以根据选项看题目
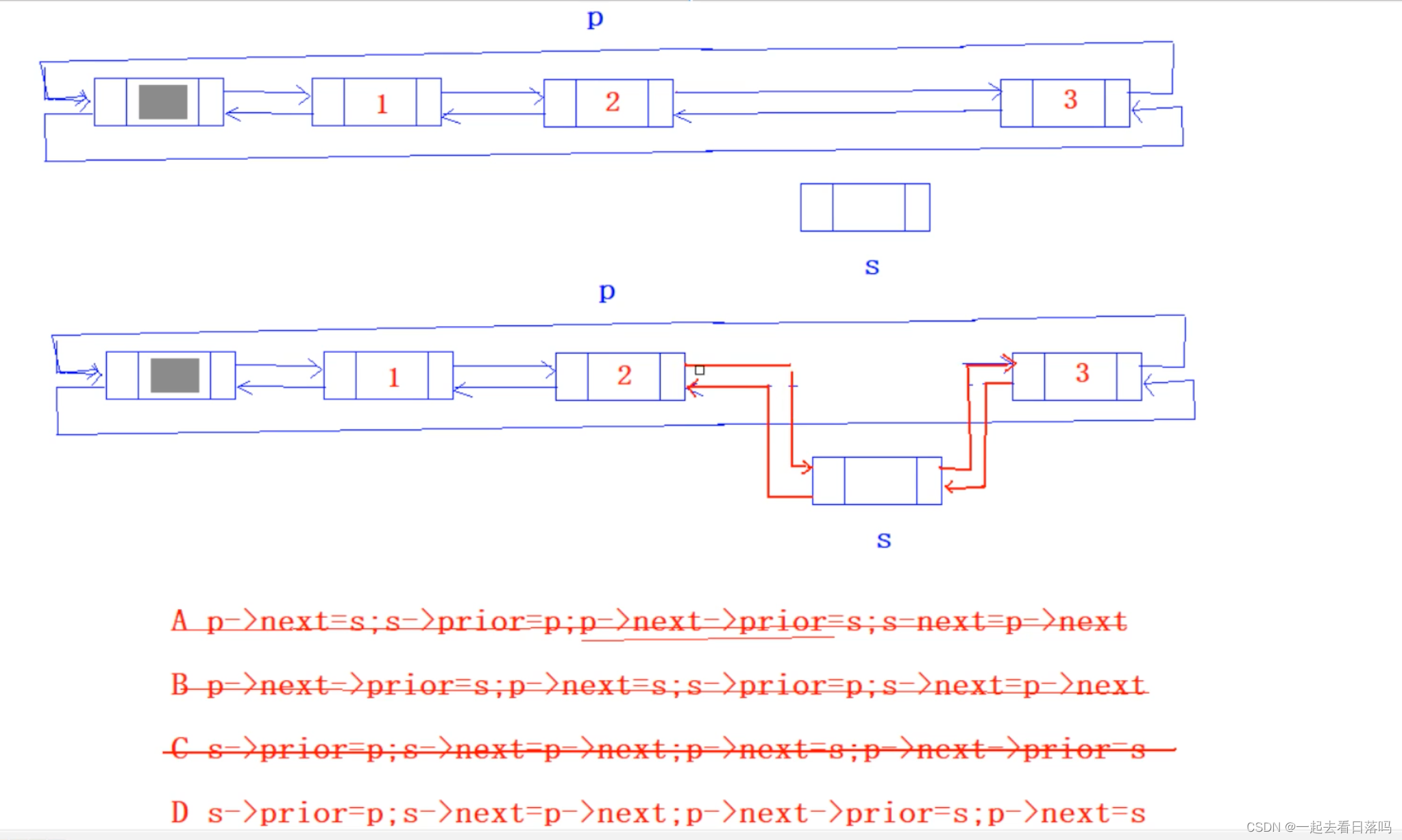
这道题的答案是D
💦第四题
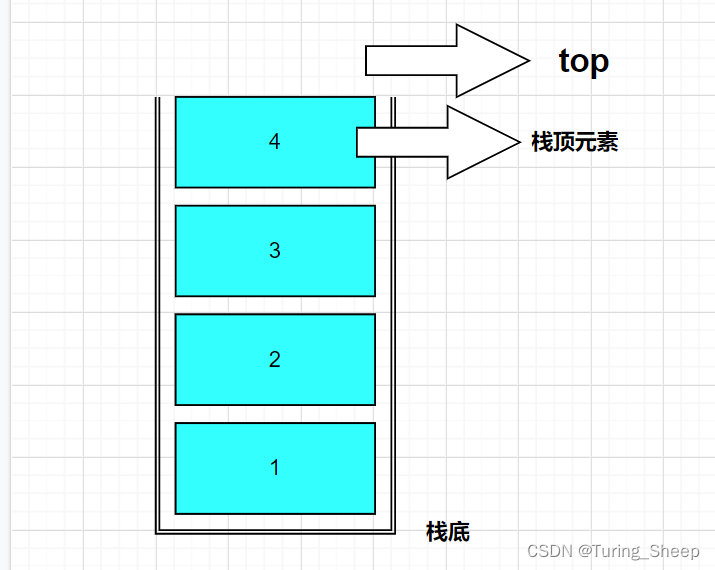
栈是一种智能在某一端插入和删除的特殊线性表,它按照后进先出的原则存储数据,先进入的数据被压入栈底,最后的数据在栈顶,若6元素为A、B、C、D、E、F出栈顺序为B、D、C、F、E、A,则S栈的最小容量为()。
A 3
B 4
C 5
D 6
这种题目也是画出图就可以知道结果了
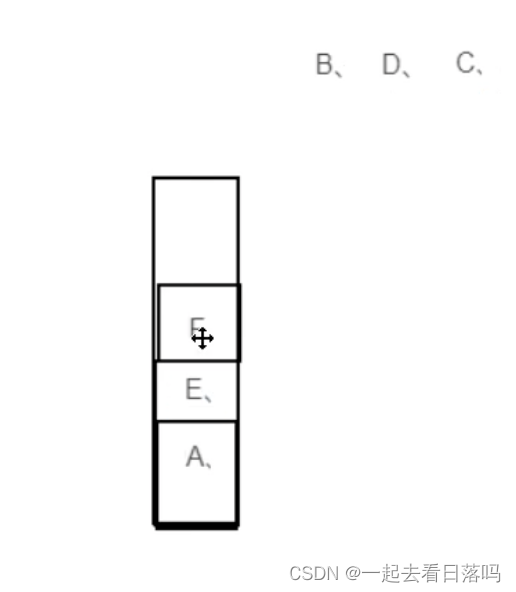
这道题的答案是A
💦第五题
现有一循环队列,其队头指针为front,队尾指针为rear;循环队列长度为N。其队内有效长度为()(假设队头不存放数据)
A (rear - front + N) % N + 1
B (rear - front + N) % N
C (rear - front) % (N + 1)
D (rear - front + N) % (N - 1)
队头不存放数据代表多一个空间不使用,数据结构一定要多画图,假设有8个空间,最多可以存储7个数据,举例子按公式算就可以了,并不需要过多思考,找反例就可以
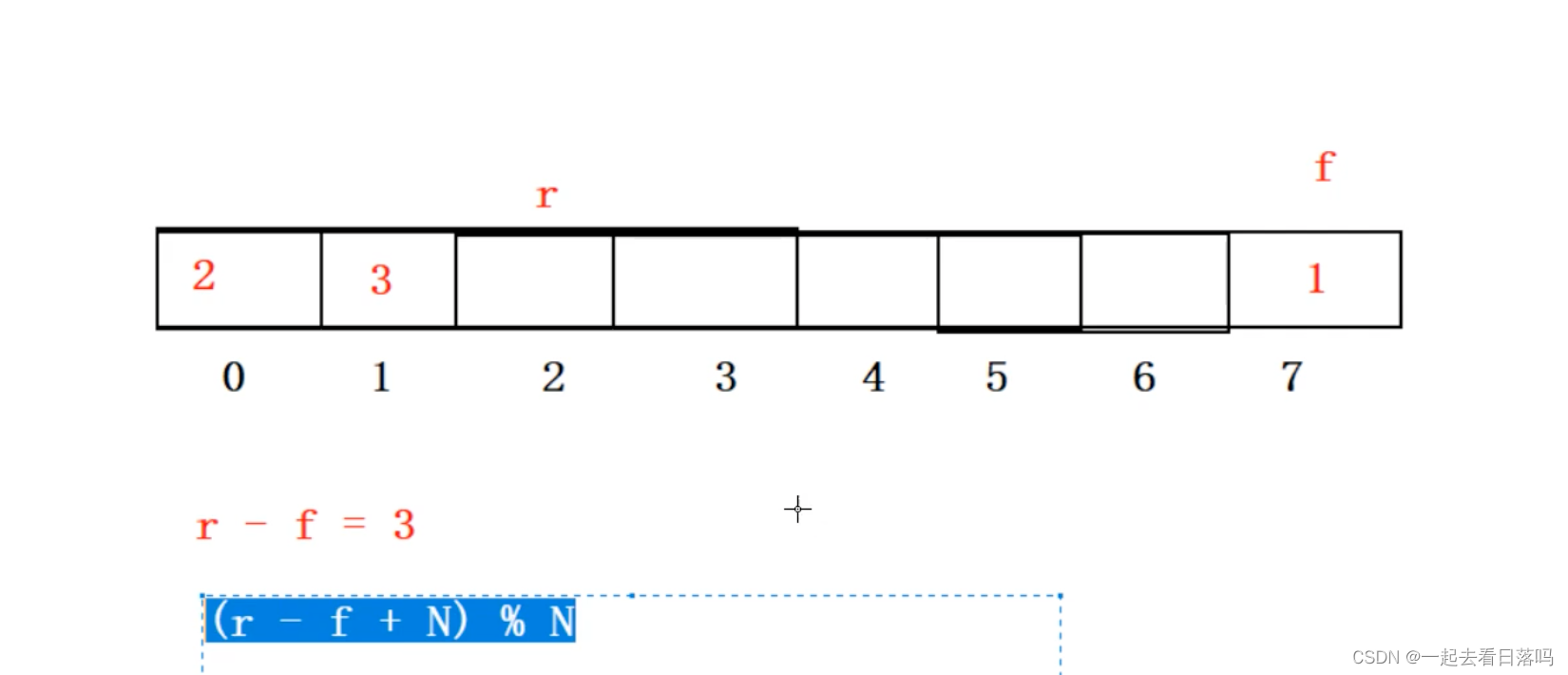
这道题的答案是B
💦第六题
下述结论中,正确的是()①只有一个结点的二叉树的度为0;②二叉树的度为2;③二叉树的左右子树可任意交换;④深度为K的完全二叉树的结点个数小于或等于深度相同的满二叉树
A ①②③
B ②③④
C ②④
D ①④
二叉树的度是所有节点中度最大的一个,只有一个节点所以度为0,所以1⃣️正确,二叉树的度可以是0 1 2 ,所以2⃣️错误,二叉树如果摆法不相同,是有序数,则两棵树不同,所以3⃣️错,完全二叉树本身是按照满二叉树的方式建立的,所以4⃣️正确
这道题的答案是D
💦第七题
若将关键字1,2,3,4,5,6,7 依次插入到初始为空的平衡二叉树 T 中,则 T 中平衡因子为 0 的分支结点的个数是( )
A 0
B 1
C 2
D 3
只要把图画出来,所有的数据结构问题都可以迎刃而解
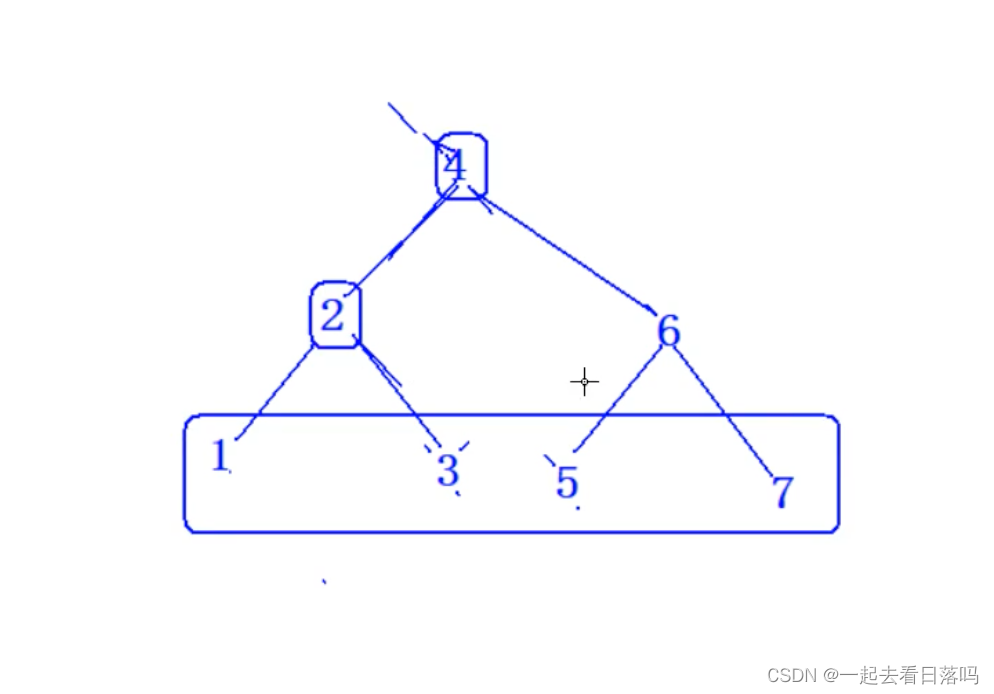
这道题的答案是D
💦第八题
初始序列为1 8 6 2 5 4 7 3一组数采用堆排序,当建堆(小根堆)完毕时,堆所对应的二叉树中序遍历序列为()
A 8 3 2 5 1 6 4 7
B 3 2 8 5 1 4 6 7
C 3 8 2 5 1 6 7 4
D 8 2 3 5 1 4 7 6
这道题是考察建堆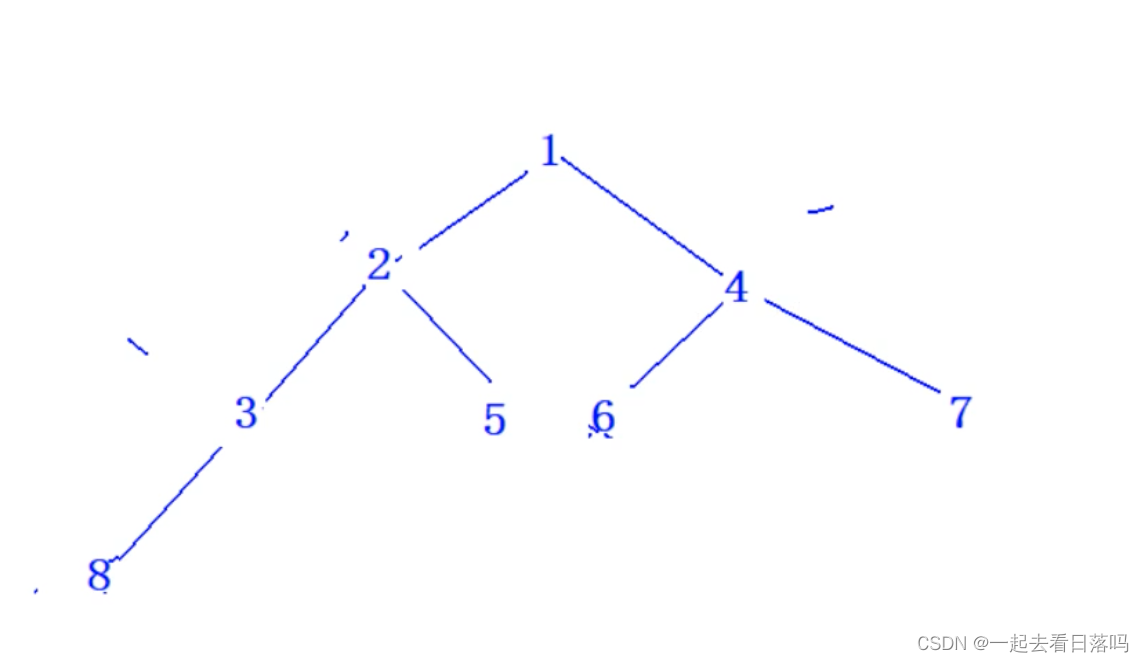
这道题的答案是A
💦第九题
解决散列法中出现冲突问题常采用的方法是()
A 数字分析法、除余法、平方取中法
B 数字分析法、除余法、线性探测法
C 数字分析法、线性探测法、多重散列法
D 线性探测法、多重散列法、链地址法
数字分析的不是常用的方法,除余法不是解决冲突,是映射发生
线性探测法、多重散列法、链地址法才是常用的方法
这道题的答案是D
💦第十题
下列选项中,不可能是快速排序第2趟排序结果的是 ()
A 2,3,5,4,6,7,9
B 2,7,5,6,4,3,9
C 3,2,5,4,7,6,9
D 4,2,3,5,7,6,9
快速排序是找到一个关键值,然后左边小于他,右边大于他,然后继续递归排序
所以C是不可以的
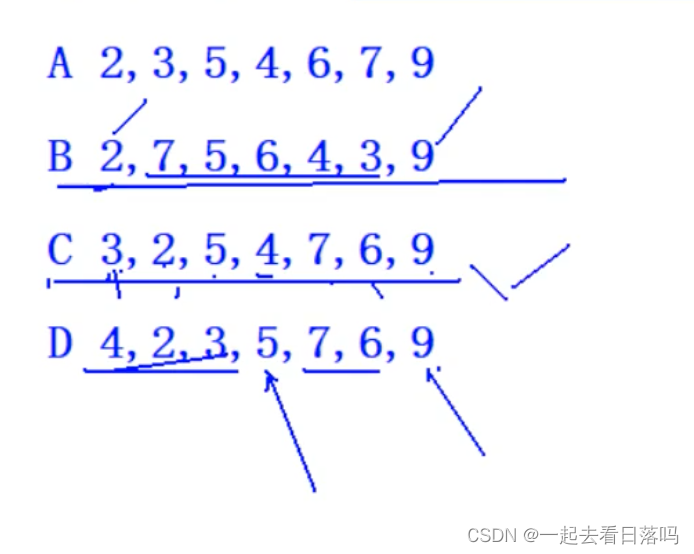
这道题的答案是C
编程题
🔥第一题
链接:字符串反转
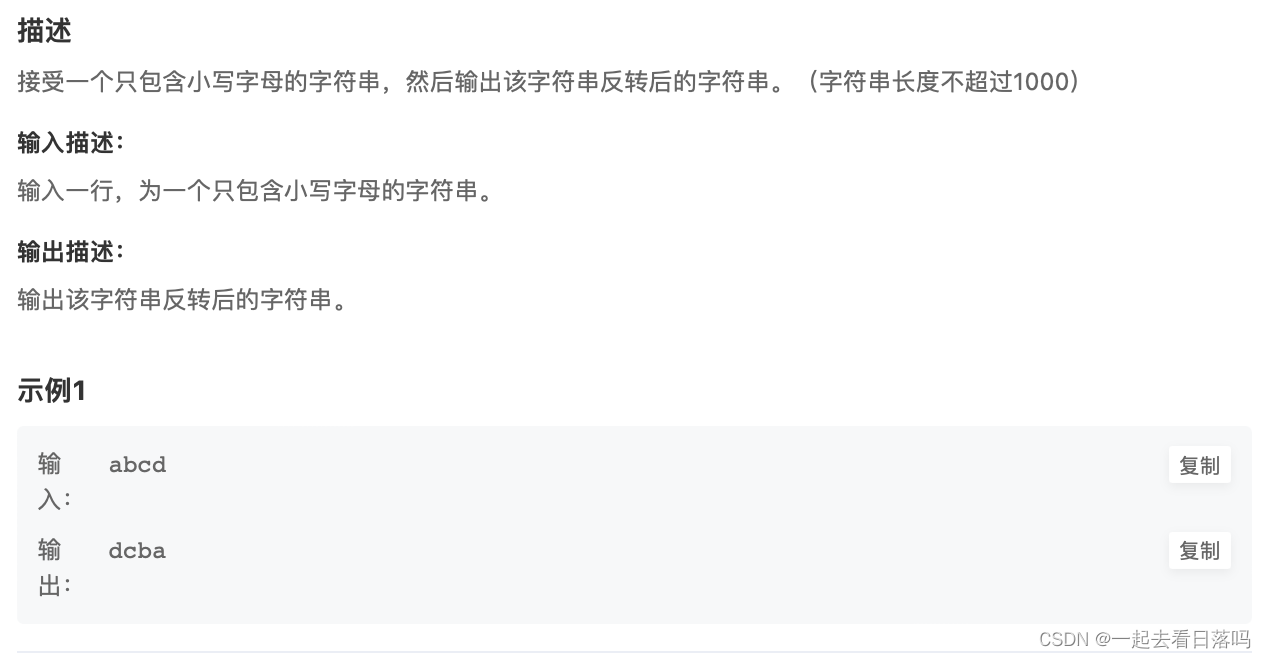
- 解题思路
字符串反转,需要交换首尾字符,设置首尾两个位置start,end,每次交换首尾字符,然后start++, end–,直到start,end相遇,反转完成。
或者直接调用库函数里面的交换
- 代码也是
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
//方法一
void strReverse_1(string &s)
{
int start = 0;
int end = s.size() - 1;
while(start < end)
{
char tmp = s[start];
s[start] = s[end];
s[end] = tmp;
start++;
end--;
}
}
//方法二
void strReverse_2(string &s)
{
reverse(s.begin(),s.end());
}
int main()
{
string s;
while(cin >> s)
{
//strReverse_1(s);
strReverse_2(s);
cout << s << endl;
}
return 0;
}
🔥第二题
链接:公共子串计算
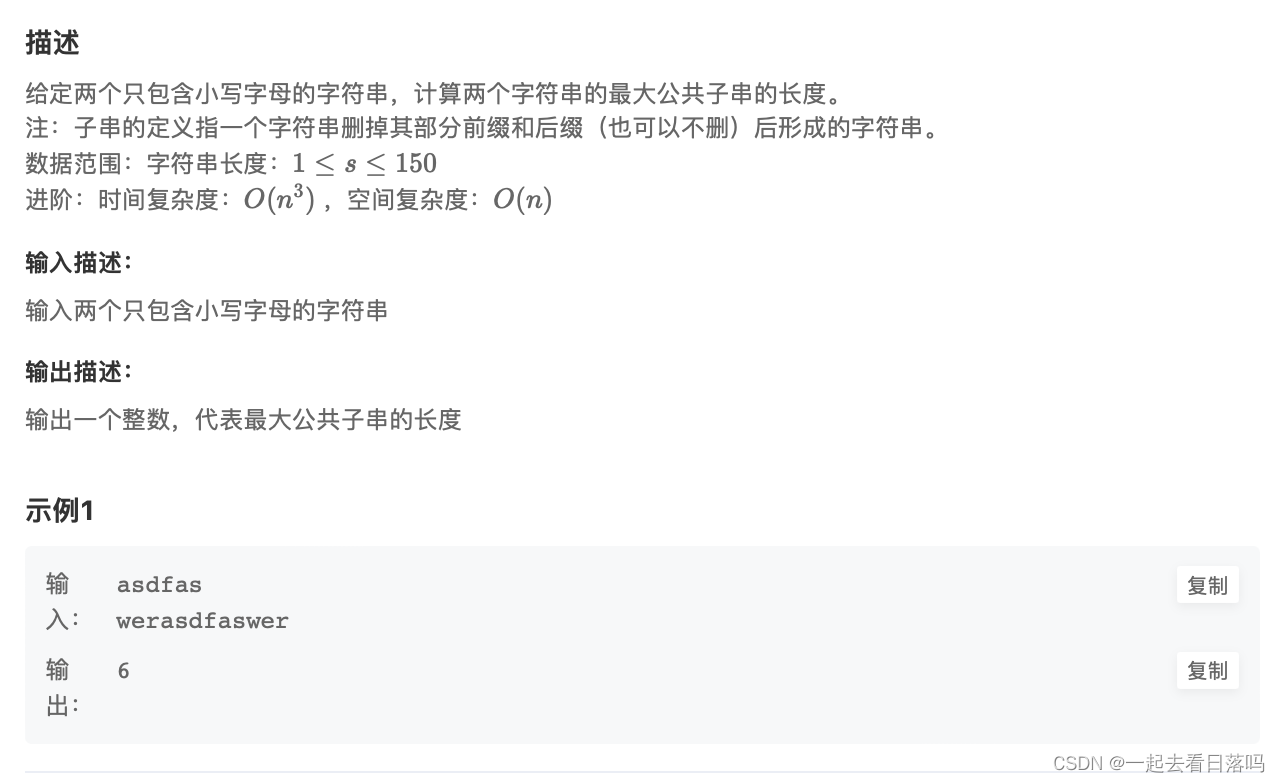
- 解题思路
求最大公共子串,使用递推实现 假设 x(i): 字符串第i个字符 y(j): 字符串第j个字符 dp[i][j]: 以x(i),y(j)结尾的最大子串长度 比如:x: “abcde” y:“bcdae” dp[2][1]: 以x(2),y(1)结尾的最大子串长度 即:x遍历到"abc", y遍历到"bc", 都以字符’c’结尾时最大公共子串为"bc" 故:当计算dp[i][j]时,首先看x(i),y(j)的值: (1): x(i) == y(j)
当前两个字符串结尾的字符相等,dp[i][j] = dp[i-1][j-1] + 1 即个它的长度加1 (2): x(i) != y(j) 当前两个字符串结尾的字符不相等,说明没有以这连个字符结尾的公共子串 即dp[i][j] = 0 (3): dp[0][j] 和 dp[i][0]表示以某个子串的第一个字符结尾,最大长度为1 如果x(0) = = y(j) 或者 x(i) == y(0), 则长度为1,否则为0 当dp中的
所有元素计算完之后,从中找打最大的值输出
- 代码演示:
#include <iostream>
#include <string>
#include <vector>
using namespace std;
int getMax(const string &s1,const string &s2)
{
int len1 = s1.size();
int len2 = s2.size();
vector<vector<int>> msc(len1,vector<int>(len2,0));
int max_len = 0;
for(int i = 0;i < len1;i++)
{
for(int j = 0;j < len2;++j)
{
if(s2[j] == s1[i])
{
if(i >= 1 && j >= 1)
msc[i][j] = msc[i-1][j-1] + 1;
else
msc[i][j] = 1;
if(msc[i][j] > max_len)
max_len = msc[i][j];
}
}
}
return max_len;
}
int main()
{
string s1,s2;
while(cin >> s1 >> s2)
{
int max_len = getMax(s1,s2);
cout << max_len << endl;
}
return 0;
}