目录

一、问题描述

二、问题分析

1.当n=1时

2.当n=2时

3.当n=3时

 4.n=4，n=5........n=n时

三、代码实现

总结

---

一、问题描述

一只青蛙一次可以跳上 1 级台阶，也可以跳上2 级。求该青蛙跳上一个n 级的台阶总共有多少种跳法。

二、问题分析

青蛙跳台阶，相信大家一开始看到这道题也是没有一点思路，但是不要担心，相信自己一定能解决这道经典题目的。

这道题我们无法直接肉眼观察出一些规律，但是我们有数学归纳法，直接看不出来，我们先写三项，三项看不出来，我们写五项，写的多了总会看出来的。

1.当n=1时

显然只有1级台阶，那么肯定只有一种跳法了。

2.当n=2时

这个时候我们有两种跳法，一种是直接跳两级，另外一种是先跳一级，再跳一级。

3.当n=3时

这个时候我们的选择可就多了，单纯的打字打出来并不是一种明智的选择，我们画一个图试试看

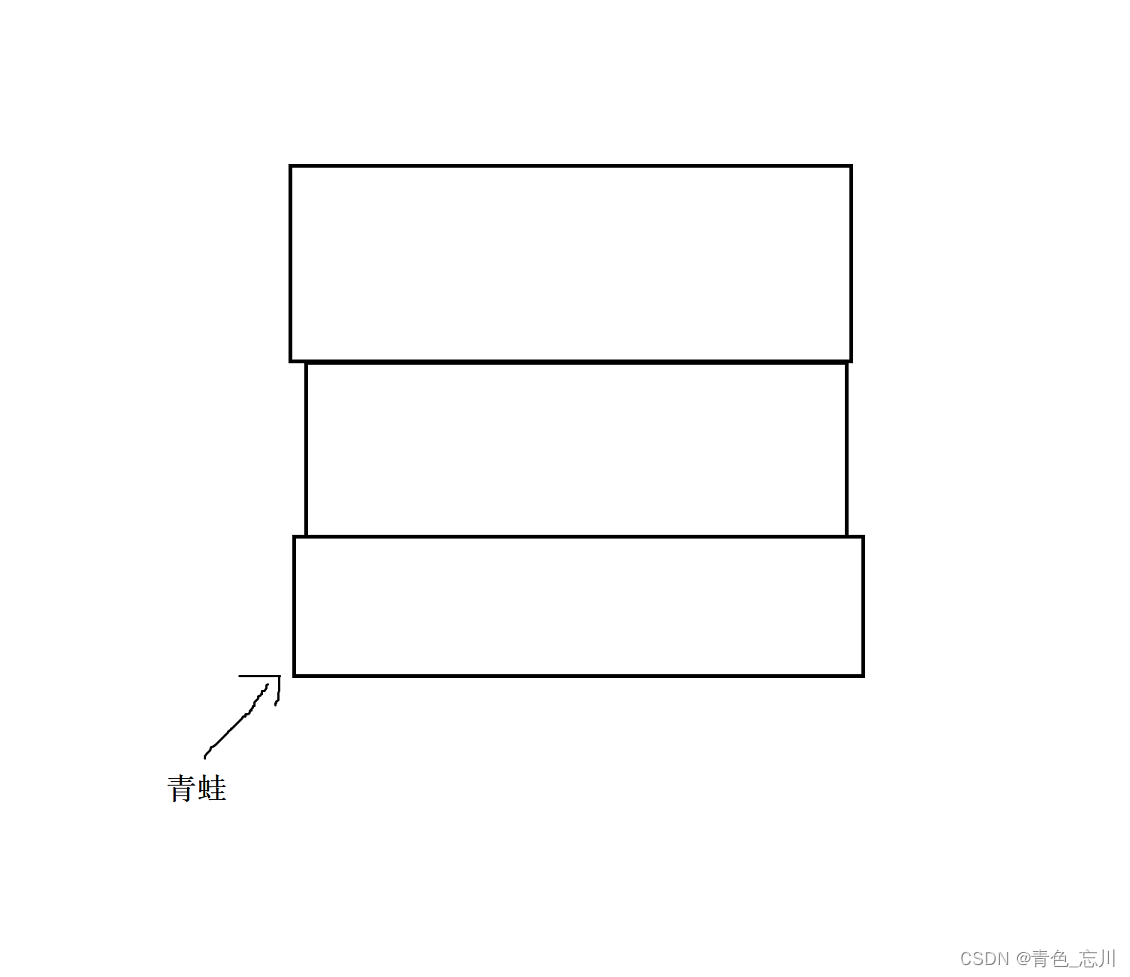
 青蛙第一次可以选择跳一层，也可以第一次跳两层，为了方便起见，不妨我们定义青蛙跳n层台阶共有f（n）种跳法

那么f（3）就有如下图所示，第一次跳1或者2，如果是1，则第二次继续跳1，或者2，如果第一次是2，那么直接跳1即可

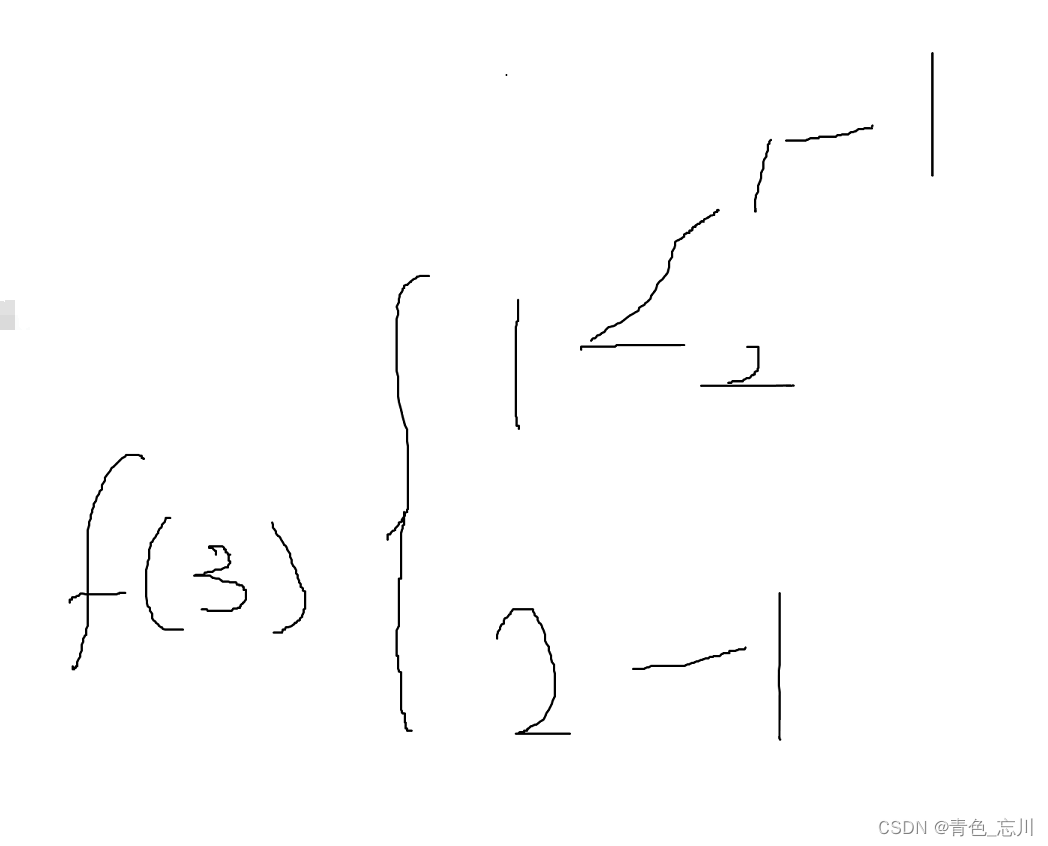
 4.n=4，n=5........n=n时

其实在这块已经有人能看到规律了，因为第一步无非就两种跳法，要么跳1，要么跳2。如果假设n个台阶有f（n）种跳法。那么则第二步有f（n-1）和f（n-2）种跳法。然后我们就发现，这不就是斐波那契数列吗。只不过就是把第二项变为2了。其余一个都没变

事实上，确实是这样的，这道题规律是比汉诺塔要好找很多的。

三、代码实现

既然本质上上就是一个斐波那契数列求第n项，只不过是第二项变为2了这种情况。那么问题迎刃而解，斐波那契数列在之前的文章中花费了大量的篇幅去详细讲解，这里给出传送门：http://t.csdn.cn/Khk31

我们直接实现代码吧

#include<stdio.h>
int f(int n)
{
	if (n == 1)
	{
		return 1;
	}
	else if (n == 2)
	{
		return 2;
	}
	else
	{
		return f(n - 1) + f(n - 2);
	}
}
int main()
{
	int n;
	scanf("%d", &n);
	int ret = f(n);
	printf("%d", ret);
	return 0;
}

---

总结

好了本期内容就讲解这么多，青蛙跳台阶和汉诺塔问题有点类似，都是需要透过现象看本质。寻找规律，从而一举制胜。