目录
- 一、引言
- 二、BP神经网络的结构与原理
- 2.1 信息前向传播
- 2.2 误差的反向传播过程
- 三、基于BP神经网络的非线性函数拟合
- 3.1 数据生成
- 3.2 神经网络拟合结果
- 四、参考文献
- 五、Matlab代码获取
一、引言
以生物学基础的BP网络为全局网络,于多变量函数逼近理论不同, BP神经网络是输入输出的映射,其优势在诸多方面比函数逼近理论要更为明显。本质上,神经网络是一个非线性系统,任意复杂的非线性函数它都能够充分逼近。良好的鲁棒性、联想记忆能力、容错性高及并行处理信息等优异特性使神经网络成为智能领域中的重要算法之一。
二、BP神经网络的结构与原理

图1所示为多层神经网络结构。其中,n表示输入层神经元个数,l表示隐含层中神经元个数,m为输出层神经元个数。ωij、ωjk为连接权值,分别表示输入层第i个神经元和隐含层第j个神经元、隐含层第j个神经元与输出层第k个神经元之间的权值。取线性函数作为输入层神经元的作用函数,即神经元的输入和输出相同。分别将隐含层和输出层神经元的上一层神经输出加权和对应作为他们的输入,激励程度和作用函数决定了各个神经元的输出。
基本BP算法包括两个方面:信息的前向传播和误差的反向传播。计算实际输出时,按从输入到输出的方向进行;而权值和阈值的修正从输出到输入的方向进行。
2.1 信息前向传播
信息前向传播过程对于图1,设各神经元的阈值为0,便于后续分析。
输入层:对于第i个神经元,其输出为 ![]()
隐含层:其第 j 个神经元的净输入为![]() ,其中输入层神经元个数为n。
,其中输入层神经元个数为n。
隐含层第 j 个神经元的输出为:![]() ,其神经元的作用函数
,其神经元的作用函数 ![]() 。
。
输出层:输出 ![]() 通过加权系数
通过加权系数![]() 向前传播到输出层第k个神经元,净输入为
向前传播到输出层第k个神经元,净输入为 ![]() , 为隐含层神经元数。
, 为隐含层神经元数。
实际网络的输出为 ![]() ,输出层第k个神经元的作用函数为
,输出层第k个神经元的作用函数为 ![]()
2.2 误差的反向传播过程
误差的方向传播,即首先由输出层开始逐层计算各层神经元的输出误差,然后根据误差梯度下降法来调节各层的权值和阈值,使修改后的网络的最终输出能接近期望值。
三、基于BP神经网络的非线性函数拟合
3.1 数据生成
利用BP网络拟合非线性函数如下:

它表示一维高斯分布高斯分布(Gaussian distribution),又称正态分布(Normal distribution)。若随机变量x服从一个数学期望为μ、方差为σ^2 的正态分布,记为N(μ,σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ= 0,σ=1时的正态分布是标准正态分布。

根据上述高斯函数得到该函数的2000组输入输出数据,从输入输出数据中随机选取1900组数据作为网络训练数据,用于网络训练。剩下的100组数据作为网络测试数据,用于测试网络的拟合性能。具体数据规划如下图所示:

3.2 神经网络拟合结果
基于BP神经网络的非线性函数拟合算法流程可以分为BP神经网络构建、BP神经网络训练和BP神经网络预测三步,如图4所示。

通过设置不同的训练要求精度,得到的拟合结果不一样,当训练精度设置为0.0000004时,神经网络训练到最佳状态,拟合输出与期望输出完全一致。

四、参考文献
[1] 吴琼. 基于BP神经网络对非线性函数拟合 [J]. 电子世界, 2018, (07): 69.
五、Matlab代码获取
完整的Matlab代码,包括非线性函数数据生成Matlab代码,可私信博主获取。
博主简介:研究方向涉及智能图像处理、深度学习等领域,先后发表过多篇SCI论文,在科研方面经验丰富。任何与算法、程序、科研方面的问题,均可私信交流讨论。

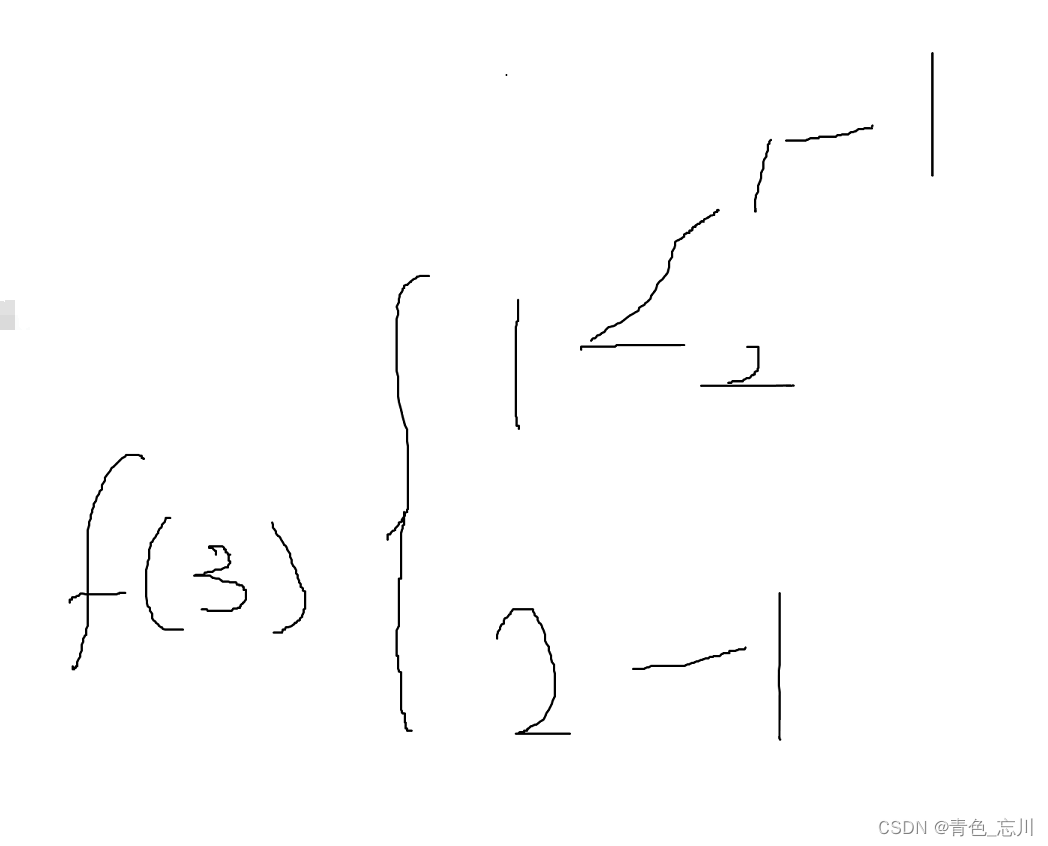




![[附源码]计算机毕业设计JAVAjsp美容院业务管理系统](https://img-blog.csdnimg.cn/cbc95f76dd35449db5f6cc9631a2281d.png)