初阶数据结构

第一章 时间复杂度和空间复杂度
第二章 动态顺序表的实现
第三章 单向链表的讲解与实现
第四章 带头双向链表的讲解与实现
第五章 栈的讲解与实现

---

---

前言

前面的章节中，我们介绍了线性表中的动态顺序表、单向链表以及带头双向链表的实现，今天我们讲解另外一种数据结构——栈。

---

一、栈

1、什么是栈？

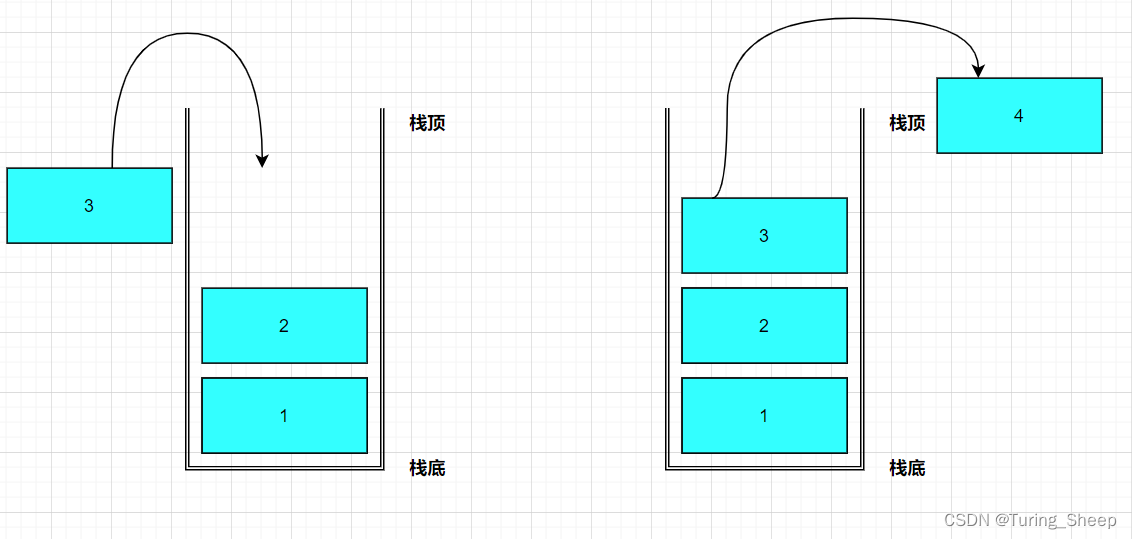
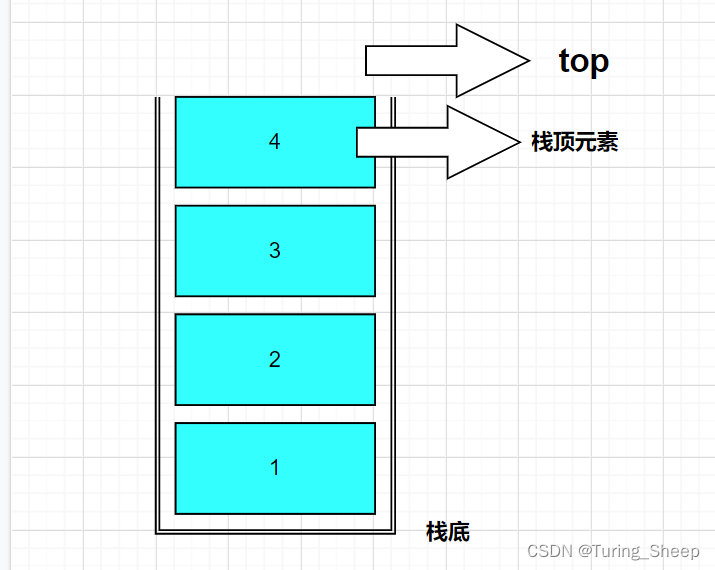
栈的逻辑结构如下所示：类似于一个桶，然后我们从栈顶的位置往里放数据。

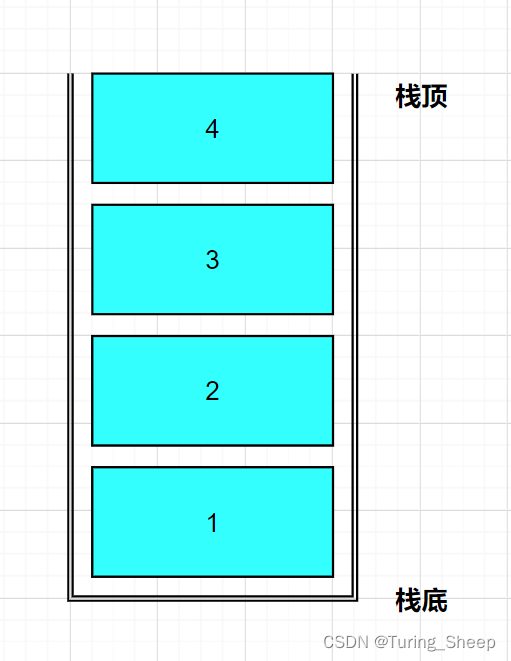
那么这个数据结构有什么特点呢？
我们从图中可以看出，我们想要取出标号为1的元素时，需要先按照4、3、2的顺序依次取出1上端的数据。因此我们便能发现，第一个放进去的数据是最后出来的，最后一个放进去的数据是第一个出来的。
那么我们将这种特点称之为：先进后出。

二、栈的定义

我们在理解了栈的逻辑结构后，我们应该如何实现呢？在回答这个问题之前，我们先将这种逻辑结构换一种表示方式：

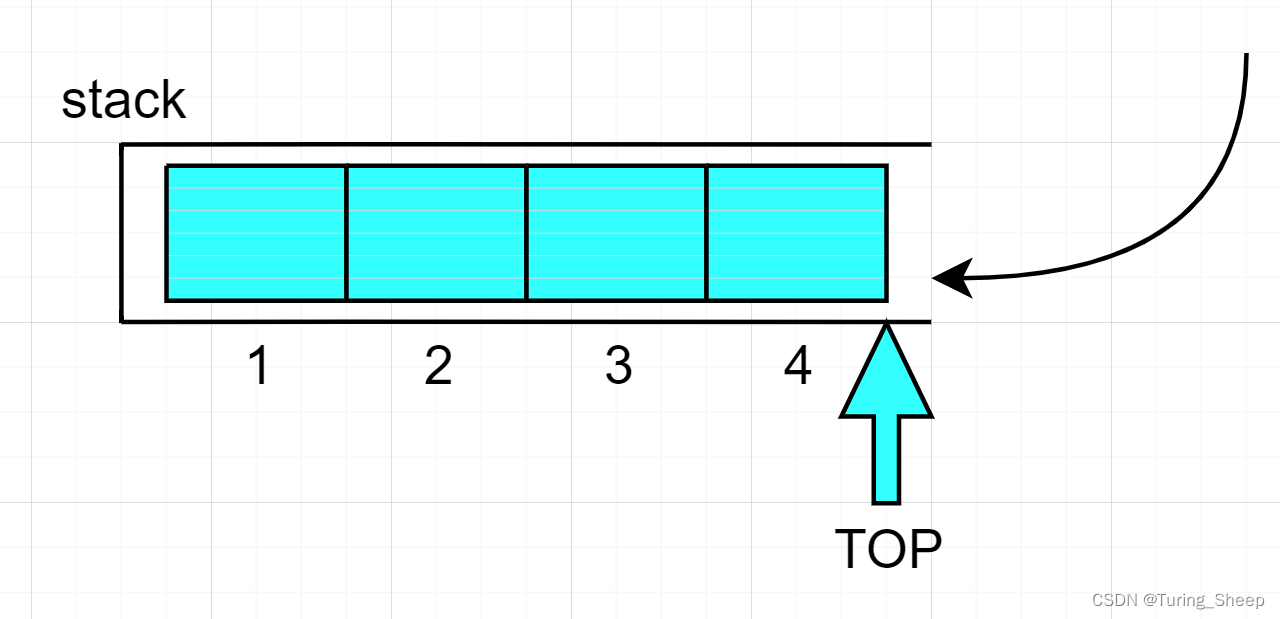
看到这种表示方式后，我们最容易想到的，用来实现栈的方式就是数组。那么我们上次用数组实现的数据结构是顺序表。既然顺序表可以用来实现栈，那么链表可以吗？
其实也是可以的，如下图所示：

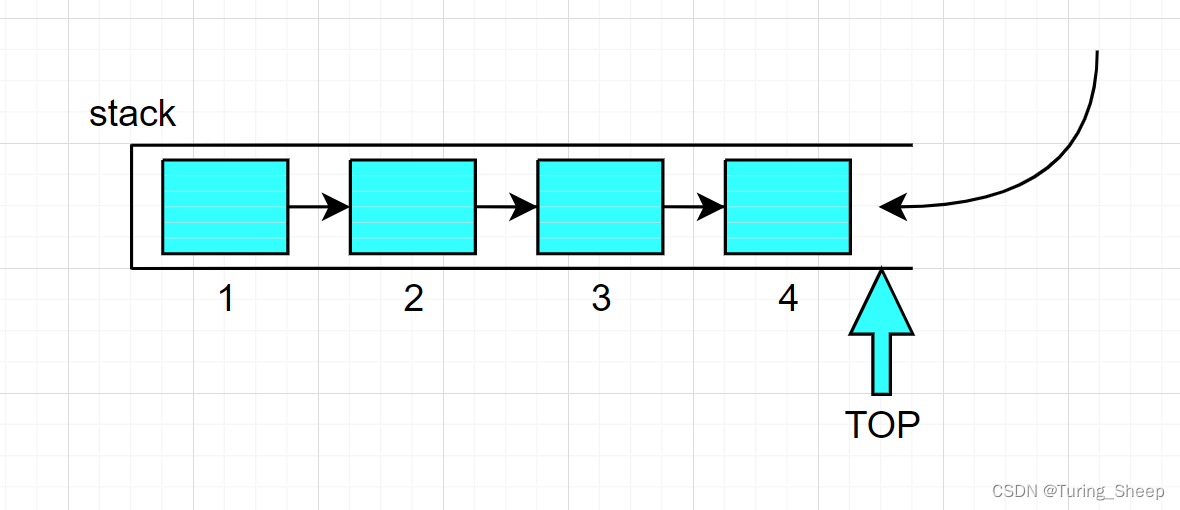
那么这两种方式哪一种更优呢？
我们发现栈这种数据结构是不存在随即插入这种方式的，因为它只能尾插。因此，顺序表的弊病之一就得以躲避了。但是我们以链表的方式来模拟的时候，我们需要不断地找尾，这个过程的时间复杂度是O(N)。或许我们可以通过事先创建一个尾指针来规避查找尾部节点的过程，但在变量的创建上，链表也会额外创建指针变量来存储地址。因此，在栈的实现上，以数组的形式来实现是比较好的。

基于上述的描述，我们就能定义一个栈了

typedef int ElementType;
typedef struct Stack
{
	ElementType* a;//指向动态数组的指针
	int top;//栈顶元素的下一个位置的下标
	int capacity;//动态数组的容量
}ST;

三、接口函数的实现

1、初始化

void StackInit(ST*ps)
{
	assert(ps!=NULL);
	ps->a=NULL;
	ps->top=ps->capacity=0;
}

将指针设置为空，将top和capacity设置为0。

2、判断是否为空

int StackEmpty(ST*ps)
{
	if(ps->top==0)
	{
		return 0;
	}
	else
	{
		return 1;
	}
}

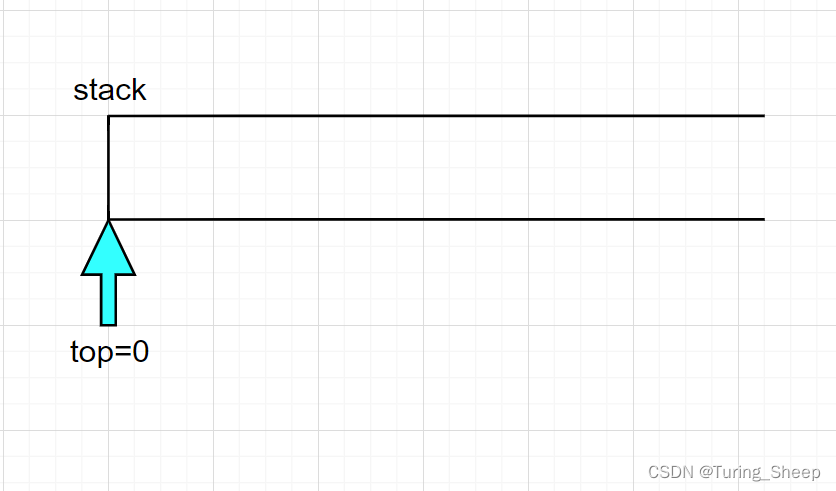
当一个栈为空的时候，恰好就是top为0的时候，因此，我们可以通过top来判断栈是否为空。

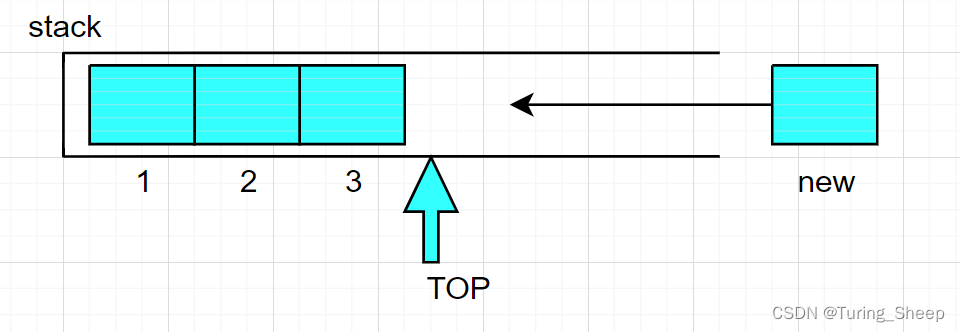
3、插入

栈种的数据插入均采用的是尾插，即在数组的末尾插入。但是在插入之前，我们需要判断一下容量的大小。当容量不足的时候，我们需要适当地进行扩容。这项操作和我们在实现顺序表的时候，所执行的操作是一样的。

void StackPush(ST* ps, ElementType dat)
{
	assert(ps!=NULL);
	if (ps->top == ps->capacity)
	{
		int newcapacity = (ps->capacity == 0) ? 4 : ps->capacity * 2;
		ElementType* temp = realloc(ps->a,sizeof(ST)*newcapacity);
		if (temp == NULL)
		{
			printf("Failed to realloc!\n");
			exit(-1);
		}
		ps->a = temp;
		ps->capacity = newcapacity;
	}

	ps->a[ps->top] = dat;//top是原数组中最后一个元素的下一个位置
	ps->top++;
}

4、删除

因为栈这种数据结构所具备的特点是元素满足先进后出，后进先出。那么何为进？即向栈种插入数据，那么何为出？即从栈中删除的数据。而每次删除的数据都是栈中最后插入的那个数据。即尾删。
但是在删除的时候我们有两点注意事项：
1、空的栈不用删除
2、top不能为负数，否则在插入数据的时候会违法访问。

上述两点的关键就是判断我们的栈是否为空。

void StackPop(ST* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	ps->top--;
}

5、元素个数

int StackSize(ST*ps)
{
	assert(ps);
	return ps->top;
}

top就相当于顺序表中的size,所以我们直接放回top的数值即可。

6、读取栈顶元素

ElementType StackTop(ST* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	return ps->a[ps->top-1];
}

7、销毁

void StackDestory(ST*ps)
{
	assert(ps!=NULL);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = 0;
	ps->a = 0;
}

直接释放即可。

四、栈中元素的访问

栈是无法像顺序表和链表那样不断地遍历元素的。因为，想要遍历元素必须取出栈顶元素，也就是说，我们必须删除栈顶的元素才能访问到下一个元素。因此，栈只能遍历一次，遍历一次之后就代表着栈已经空了。
除此以外，元素的访问顺序和插入顺序是相反的。
比如我们是按照1，2，3，4的顺序插入，那么访问的顺序就是4,3,2,1。
那么我们如何访问呢？如下图所示：

ST stack;//定义一个栈
StackInit(&stack);//初始化一个栈
//向栈中插入数据
StackPush(&stack,1);
StackPush(&stack,2);
StackPush(&stack,3);
StackPush(&stack,4);
StackPush(&stack,5);
//通过访问栈顶、删除栈顶的循环方式访问栈中的每一个元素。
while(!StackEmpty(&stack))
{
	printf("%d ",StackTop(&stack));
	StackPop(&stack);
}
StackDestory(&stack);//销毁栈