为什么需要了解偏好强化学习

为什么需要了解偏好强化学习？目前强化学习主流的方法都是基于奖励的，强化学习优化目标是长期的累计奖励。而如何设计一个好的奖励函数通常需要大量专家领域知识。并且需要考虑提出的奖励函数是否会影响学习过程，比如学习速度等等问题。在有些场景也并不是能够很好地去定义出这样一个奖励。

对于实际业务问题，业务本身比较复杂，传统解决方法(比如行为树)如果不好，那也不能基于数据去做一些offline RL。并且如果不好给定奖励函数的话，通常会采用模仿学习的方法。但是也存在一些场景人类专家也不能给出一些确切的行为，因此也不能去做一些模仿学习，比如在机器人领域控制电机的电流进而控制机械臂，人类专家无法直接给出电流的参考示例。直接人类给出动作的代价相比于给出偏好的代价是更高的。还有一些场景动作空间巨大，比如电网调度领域，动作空间高达几万个等等的一些传统解决方案很棘手的场景中，可以考虑去采用偏好强化学习来作为一种初始化网络参数，或者微调修复性能的方法。

随着生产物质的丰富，用户对于个性化追求将愈发强烈。如何将用户的个性化偏好进行量化，进而更好地服务用户(比如用GPT作为智能家居中控，给用户提供个性化的全家智能)。比如在游戏AI领域，如何基于用户反馈，设计出拟人性的智能体，或者是符合玩家兴趣爱好的智能体，或者依据玩家偏好变化而变化的NPC都是未来的发展趋势。

什么是偏好强化学习

想要去解决一个问题，首先需要去寻找的就是优化目标。在强化学习里面的优化目标就是奖励函数，因此想要待解决的问题用强化学习方法来求解，就需要将优化目标与奖励函数挂钩。而基于专家经验设计的奖励函数通常会面临四个问题：1. Reward Hacking: 只管最大化奖励分数，不考虑实际情况。2. Reward Shaping: 平衡goal definition和guidance task。3. Infinite Rewards: 存在一些case，是坚决不允许发生的。虽然现在有mask可以去做，但是也有一些问题其实是没有办法用mask去做的，只有做了之后才能验证是否违反了硬约束条件。4. Multi-objective Trade-off: 如果需要考虑多个优化目标
当然也有一些方法在设计一些内在的奖励，来处理这样一个问题。然而设计一个好的内在奖励其实也是很困难的。

偏好强化学习(Preference-Based Reinforcement Learning, PbRL)直接基于专家的反馈进行学习，并不需要设计奖励函数，并且对于人类对于专业领域的需求也比较少，因为给一个确切的数值奖励给智能体，而是一个比较值。PbRL的关键在于说把强化学习里面，对于奖励，从一个数值的反馈信号变成了一个偏好的反馈信号。想要构建偏好强化学习的优化过程，我们还需要去定义一些符号，和我们能够拿到的数据集合：

• $z_i\succ z_j$: 数据$z_i$是strictly preferred。
• $z_i\sim z_j$: 数据偏好是无法区分的 indifferent。
• $z_i⪰z_j$: 数据$z_i$是weakly preferred。

基于偏好的马尔科夫决策过程（Markov decision processes with preferences，MDPP）

一个MDPP可以定义成$(S,A,\mu ,\delta ,\gamma ,\rho )$：

• $S$ 状态空间
• $A$ 动作空间
• $\mu (s)$ 初始状态分布
• $\delta$ 状态转移模型 $\delta (s^{\prime }|s,a)$
• $\gamma$ 折扣因子

一条采样的轨迹(trajectory)可以表示为:

τ = { s 0 , a 0 , s 1 , a 1 , … , s n − 1 , a n − 1 , s n } \boldsymbol{\tau}=\{s_0,a_0,s_1,a_1,\ldots,s_{n-1},a_{n-1},s_n\} τ={s0​,a0​,s1​,a1​,…,sn−1​,an−1​,sn​}

$\rho ({\tau }_i\succ {\tau }_j)$定义为给定轨迹$({\tau }_i,{\tau }_j)$下，${\tau }_i\succ {\tau }_j$的概率。智能体可以接收到一个偏好集合：

ζ = { ζ i } = { τ i 1 ≻ τ i 2 } i = 1... N \zeta=\{\zeta_i\}=\{\tau_{i1}\succ\tau_{i2}\}_{i=1...N} ζ={ζi​}={τi1​≻τi2​}i=1...N​

并且假设偏好是严格偏好，也就是有：

$$\rho ({\mathbf{\tau }}_i\succ {\mathbf{\tau }}_j)=1-\rho ({\mathbf{\tau }}_j\succ {\mathbf{\tau }}_i)$$

注意：这里并没有假设一个奖励的数值信号$r(s,a)$。

如何基于人类反馈的偏好来优化策略呢？

基于人类反馈的优化框架如下图所示：

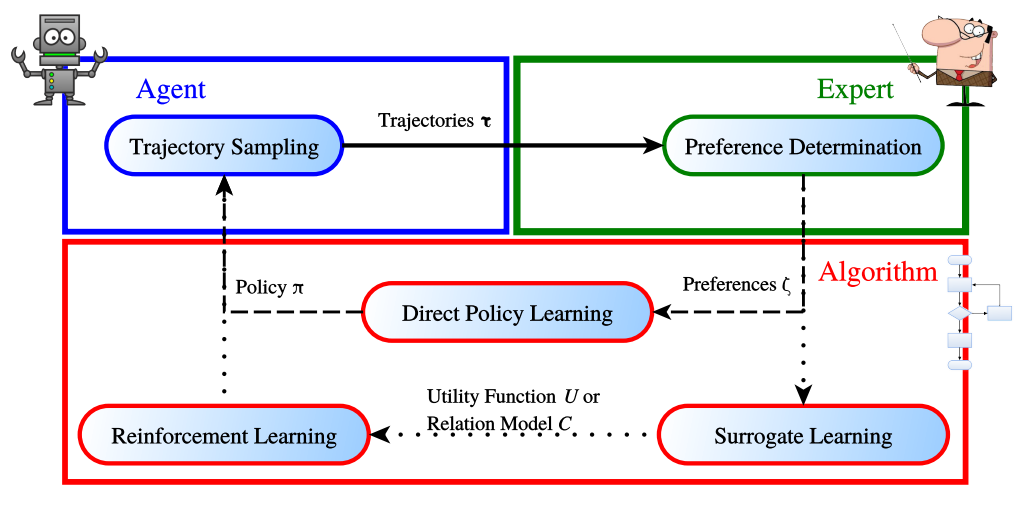
对于一个智能体来说，一个通用的目标是，在一个给定的集合$\zeta$中去寻找到一个策略${\pi }^{\ast }$，能够最大化人类偏好。${\tau }_1\succ {\tau }_2\in \zeta$需要满足的条件是：

$${\mathbf{\tau }}_1\succ {\mathbf{\tau }}_2\iff \underset{\pi }{\mathrm{Pr}}({\mathbf{\tau }}_1)>{\mathrm{Pr}}_{\pi }({\mathbf{\tau }}_2)$$

其中

$$\underset{\pi }{\mathrm{Pr}}(\mathbf{\tau })=\mu (s_0)\prod _{t=0}^{|\mathbf{\tau }|}\pi (a_t\mid s_t)\delta (s_{t+1}\mid s_t,a_t)$$

基于轨迹(trajectory)的最大化偏好问题可以描述为：

$${\tau }_1\succ {\tau }_2\iff {\pi }^{\ast }=\arg \underset{\pi }{\max }\left(\underset{\pi }{\mathrm{Pr}}({\tau }_1)-\underset{\pi }{\mathrm{Pr}}({\tau }_2)\right)$$

到此，我们就可以定义出一个最小化偏好损失函数：

$$L(\pi ,{\mathbf{\tau }}_1\succ {\mathbf{\tau }}_2)=-\left(\underset{\pi }{\mathrm{Pr}}({\mathbf{\tau }}_1)-\underset{\pi }{\mathrm{Pr}}({\mathbf{\tau }}_2)\right)$$

在有多个偏好相互比较的关系下，损失函数可以表示为：

$$\mathbf{L}(\pi ,\zeta )=(L(\pi ,{\zeta }_0),L(\pi ,{\zeta }_1),\dots ,L(\pi ,\zeta {}_n))$$

表示为权重加和的方式则为：

$$\mathcal{L}(\pi ,\zeta )=\sum _{i=1}^N{\alpha }_{i}L(\pi ,{\zeta }_i)$$

反馈类型分类

1. 动作偏好(action preference): 对于给定的相同状态，比较两个动作。这种方法无法处理短期偏好与长期偏好的关系。
2. 状态偏好(state preference): $s_{i1}\succ s_{i2}$表示相比于状态$s_{i2}$，人类更偏好状态$s_{i1}$。
3. 轨迹偏好(trajectory preference): ${\tau }_{i1}\succ {\tau }_{i2}$表示轨迹${\tau }_{i1}$优于轨迹${\tau }_{i2}$。轨迹偏好里一个重要问题就是信用分配问题(temporal credit assignment problem)。

学习算法分类

近似策略分布(Approximating the Policy Distribution)

对于给定的trajectory $\zeta$，基于参数化的策略分布$\mathrm{Pr}(\pi |\zeta )$产生不同的策略${\pi }_1,{\pi }_2$，再基于产生的不同的策略来产生不同的trajector ${\tau }_1,{\tau }_2$, 再给定人类评判偏好，存储偏好轨迹。最后产生能够最大化轨迹偏好的策略$argma{x}_{\pi }Pr(\pi |\zeta )$。

比较和排序策略(Comparing and Ranking Policies)

给定策略集合，在策略集合中直接进行偏好排序，选取获取偏好排序最大的策略作为最终策略进行输出：

学习偏好模型(Learning a Preference Model)

直接学一个偏好模型：$C(a\succ a^{\prime }|s)$，策略为贪婪策略。类似DQN，在这里是直接计算偏好函数，然后基于偏好函数来直接求解策略。

学习奖励函数(Learning a Utility Function)

基于偏好计算一个奖励函数$U(\tau )$，在许多场景中可以拆分为 $U(s,a)$。策略求解即为最大化奖励的过程。 这也是目前主流的求解方案：

总结这四类方法就是：1. 构建一个产生策略的函数$\theta$，一最大化偏好轨迹来优化$\theta$。2. 给定一个策略集合，基于偏好，直接在策略集合中选取能够产生人类偏好最大的策略。3. 学习一个偏好模型$C(a\succ a^{\prime }|s)$, 基于这个偏好模型直接贪婪产生策略。4. 学习奖励函数，策略基于奖励函数进行优化。

近期工作

Deep Reinforcement Learning from Human Preference（2023）

• Deep Reinforcement Learning from Human Preference

这篇文章主要贡献是用于比较困难的游戏场景中：

奖励预测器损失函数可以表示为：

$$\hat{P}[{\sigma }^1\succ {\sigma }^2]=\frac{\exp \sum \hat{r}(a_t^1,a_t^1)}{\exp \sum \hat{r}(o_t^1,a_t^1)+\exp \sum \hat{r}(o_t^2,a_t^2)}$$

$$\log (\hat{r})=-\sum _{({\sigma }^1,{\sigma }^2,\mu )\in \mathcal{D}}\mu (1)\log \hat{P}[{\sigma }^1\succ {\sigma }^2]+\mu (2)\log \hat{P}[{\sigma }^2\succ {\sigma }^1]$$

人类偏好的不稳定性，会导致奖励预测器的偏差和方差都受到一定的影响。

实验结果：

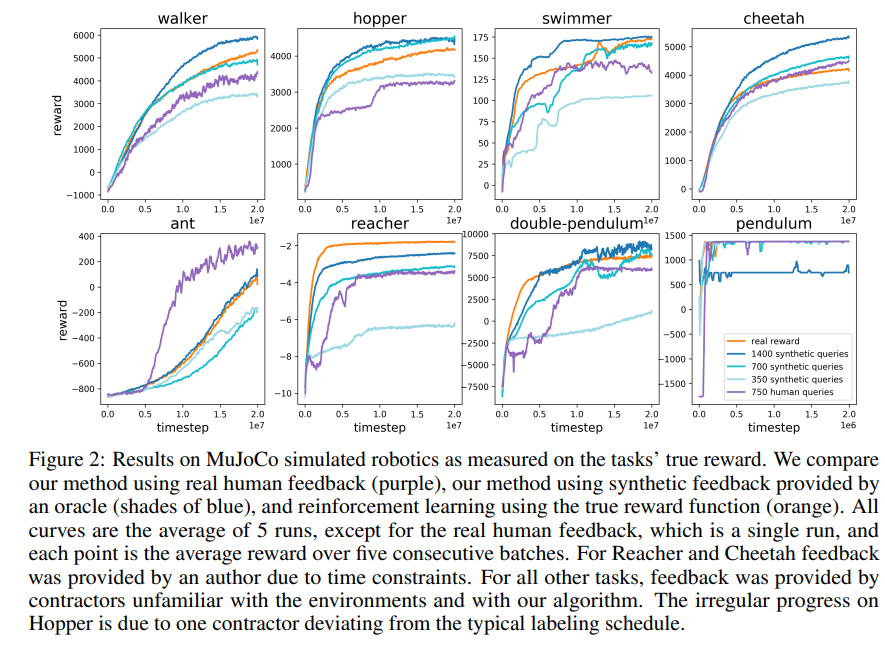
Preference Transformer: Modeling Human Preferences using Transformers for RL（2023）

• Preference Transformer: Modeling Human Preferences using Transformers for RL

这篇文章主要用于解决非马尔科夫性

整体框架图：

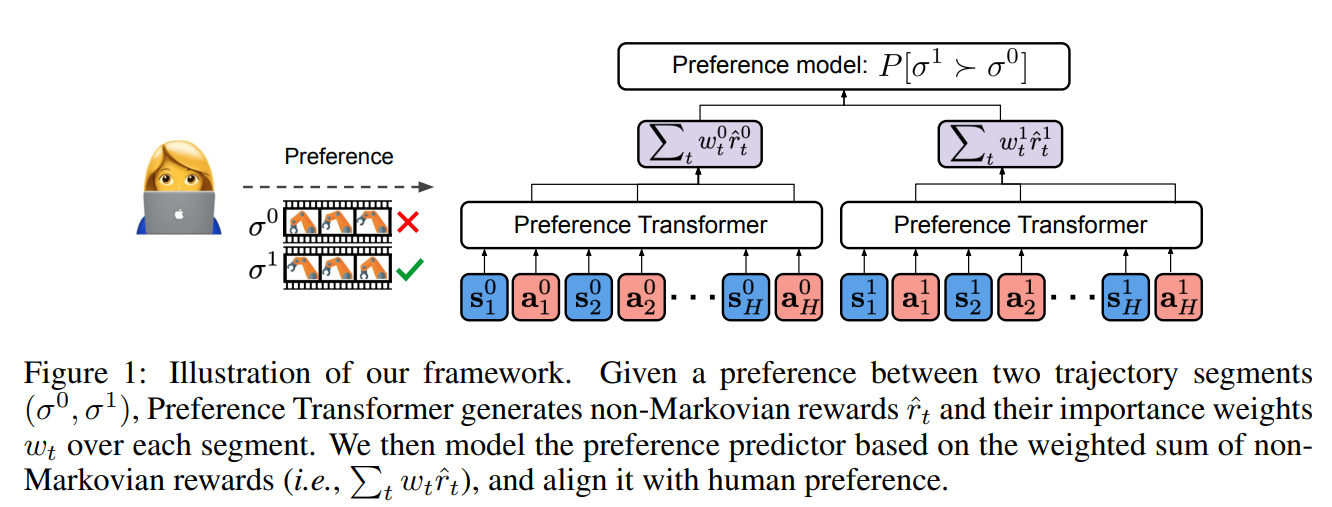
Preference Transformer局部：

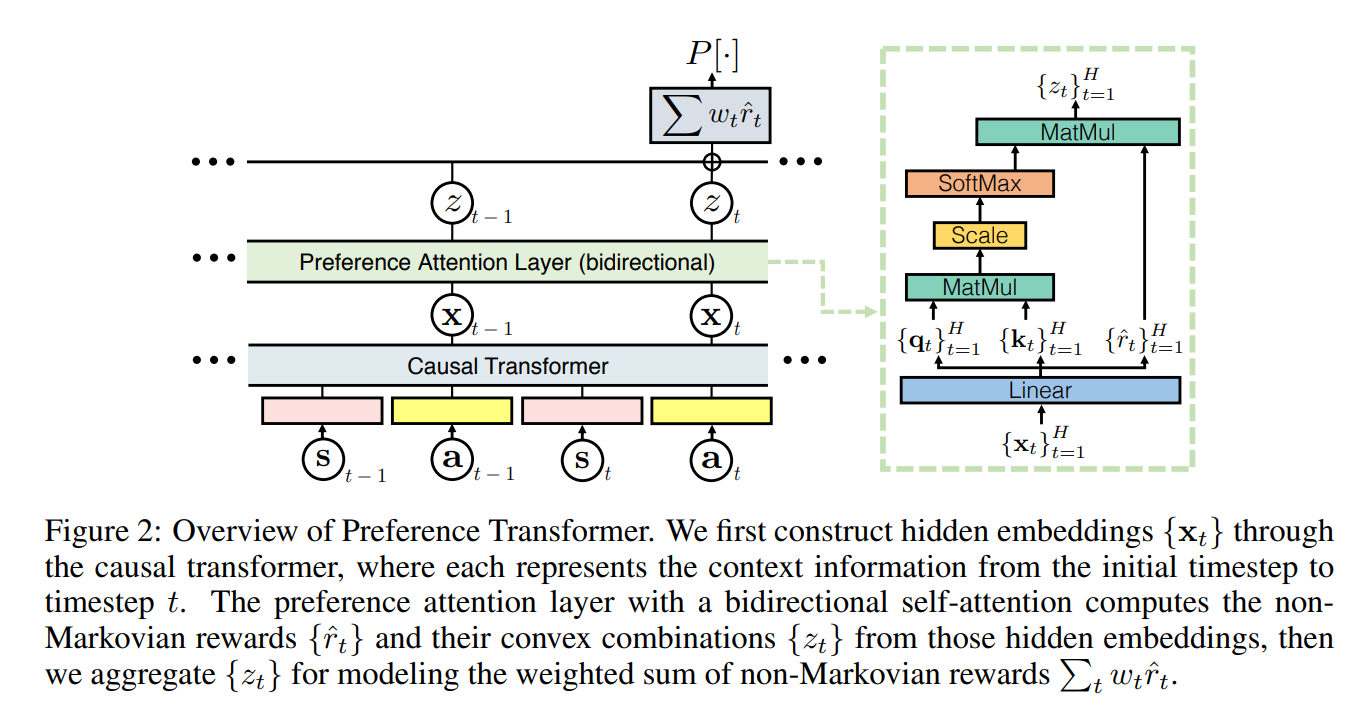
注意奖励在Linear层就已经进行了预测，后续输出是对trajectory奖励的加权。

在实验部分，作者设计了一系列的评估指标，用于确定Preference Transformer确实是学到了中间的关键步骤奖励，也就是确实进行了置信分配。

更多相关文章

• Tencent AI Lab：DEPLOYING OFFLINE REINFORCEMENT LEARNING WITH HUMAN FEEDBACK（2023）
• UC Berkeley：Principled Reinforcement Learning with Human Feedback from Pairwise or K-wise Comparisons（2023）
• OpenAI: Deep reinforcement learning from human preferences (2023)
• UC Berkeley：Preference Transformer: Modeling Human Preferences using Transformers for RL（2023）
• DeepMind: Improving Multimodal Interactive Agents with Reinforcement Learning from Human Feedback（2022）
• Humans are not Boltzmann Distributions: Challenges and Opportunities for Modelling Human Feedback and Interaction in Reinforcement Learning（2022）
• Google：Offline Reinforcement Learning from Human Feedback in Real-World Sequence-to-Sequence Tasks（2021）
• Explore, Exploit or Listen: Combining Human Feedback and Policy Model to Speed up Deep Reinforcement Learning in 3D Worlds （2021）
• Human feedback in continuous actor-critic reinforcement learning（2019）
• Stanford: Deep Reinforcement Learning from Policy-Dependent Human Feedback （2019）
• A Survey of Preference-Based Reinforcement Learning Methods （2017）
• Nature: Reinforcement learning improves behaviour from evaluative feedback（2015）
• Augmenting Reinforcement Learning with Human Feedback（2011）