学习目标:
我会按照以下步骤学习高斯求积公式简介:
-
理解积分的概念:学习什么是积分以及积分的几何和物理意义,如面积、质量、电荷等概念。
-
掌握基本的积分技巧:掌握基本的积分公式和技巧,如换元法、分部积分、三角换元等。
-
了解数值积分的基本思想:了解为什么需要数值积分以及数值积分的基本思想,包括使用一些数值方法来近似计算积分值。
-
学习高斯求积公式的推导:学习高斯求积公式的推导过程和基本思想,理解高斯求积公式的原理和优点。
-
掌握高斯求积公式的计算方法:掌握高斯求积公式的计算方法,包括节点和权重的计算、计算公式的选择、误差估计等。
-
练习高斯求积公式的应用:通过大量的练习和实例,熟练掌握高斯求积公式的应用,包括一般函数和特殊函数的求积、复合积分的计算等。
-
掌握高斯-勒让德求积公式:学习高斯-勒让德求积公式,了解其基本思想和应用场景。
-
了解高斯-拉盖尔求积公式和高斯-埃尔米特求积公式:了解高斯-拉盖尔求积公式和高斯-埃尔米特求积公式,了解它们的特点和应用场景。
-
拓展高斯求积公式的应用:了解高斯求积公式在更广泛的应用中的具体表现,如在微分方程数值解法中的应用等。
通过以上学习步骤,可以深入了解高斯求积公式的基本思想和应用,从而更好地应用于实际问题中。

高斯型求积公式:
高斯型求积公式是一类通过将被积函数在特定节点处的函数值和导数值进行线性组合得到积分近似值的数值积分方法。其形式一般为:

其中,$w(x)$ 称为权函数,$f(x)$ 是被积函数,$x_i$ 是积分节点,$w_i$ 是系数。根据高斯型求积公式的不同,节点和系数的选择也会有所不同。
高斯型求积公式具有代数精度,即对于阶数不超过 $2n-1$ 的多项式,都能精确积分。这是由于权函数和积分节点的选取,使得高次项的导数在节点处为零,从而被积函数和多项式的误差项同阶消失。
常见的高斯型求积公式包括高斯-勒让德求积公式、高斯-拉盖尔求积公式、高斯-赛德尔求积公式等。这些求积公式都有其特定的节点和系数选择,因此在使用时需要根据具体的被积函数进行选择。

正交多项式:
正交多项式是指在某个区间上的一组多项式函数,它们的内积在这个区间上为零,而它们自己在这个区间上是非零的。也就是说,正交多项式的任意两个不同的多项式函数之间在这个区间上的内积都等于零,而每个多项式函数自己在这个区间上的内积不为零。
常见的正交多项式包括勒让德多项式、切比雪夫多项式、拉盖尔多项式、埃尔米特多项式等。
在数值积分中,正交多项式有着重要的应用。由于正交多项式的性质,可以使用它们来构造高精度的数值积分公式。其中,高斯型求积公式就是一种基于正交多项式的数值积分方法。
 带权正交:
带权正交:
带权正交是指在一定权重函数下的正交多项式。在一般的正交多项式的定义中,正交是指多项式之间在某种加权意义下正交,即两个不同的多项式在某种权重函数下的内积为0。而带权正交中,内积的定义不再是简单的积分,而是对函数乘上一个权重函数再积分,这个权重函数可以是任意的非负可积函数。这样,我们就可以在不同的加权意义下定义正交多项式,使得它们在不同的场合下具有不同的性质和应用。
 勒德让多项式:
勒德让多项式:
勒让德多项式(Legendre polynomial)是一种正交多项式,它的形式为:

其中$n$为多项式的次数,$x$为自变量。
勒让德多项式在数学中具有广泛的应用,例如求解微分方程、计算特殊函数、数值计算中的高斯求积等。
勒让德多项式具有如下性质:
-
零点是对称的:$P_n(-x) = (-1)^nP_n(x)$;
-
正交性:在区间$[-1,1]$上,不同次数的勒让德多项式两两正交,即:
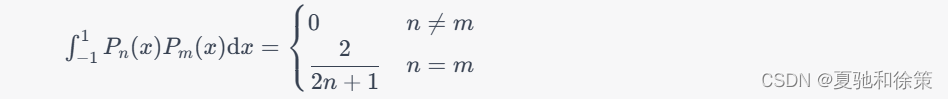
这里的正交性是指在带权内积下的正交性,即:
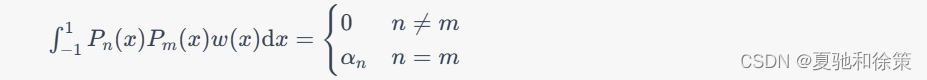
其中$w(x)$为权函数,$\alpha_n$是常数;
-
归一化:勒让德多项式可以通过如下方式进行归一化:

归一化后的勒让德多项式$\widetilde{P}_n(x)$满足:

其中$\delta_{nm}$为Kronecker delta符号,当$n=m$时为1,否则为0。

切比雪夫多项式是指满足以下递推式的多项式序列:
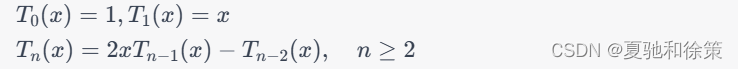
切比雪夫多项式在数值分析和逼近论中有着广泛的应用。
切比雪夫多项式是一种正交多项式,其正交性定义在区间$[-1,1]$上,即对于不同的$m$和$n$,有:
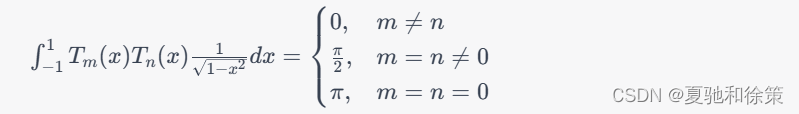
切比雪夫多项式具有许多优良的性质,如零点分布、逼近等等。在数值分析中,切比雪夫多项式还被用于构造切比雪夫插值多项式和切比雪夫拟合多项式,以及在求解常微分方程、偏微分方程等方面的应用。
总结:
以下是高斯求积公式简介的重点、难点和易错点的总结:
重点:
- 高斯型求积公式的基本形式是 $\int_{-1}^1 f(x)w(x)dx \approx \sum_{i=1}^n A_i f(x_i)$,其中 $w(x)$ 是权函数,$A_i$ 和 $x_i$ 是待定系数和节点。
- 正交多项式是高斯型求积公式的重要理论基础,正交多项式具有相互正交和单位范数的性质,可用于求解待定系数和节点。
- 常见的正交多项式包括勒让德多项式和切比雪夫多项式,不同的正交多项式适用于不同类型的权函数。
- 带权正交可用于求解一般区间上的高斯型求积公式,常见的带权正交包括拉盖尔-高斯、勒让德-高斯和切比雪夫-高斯等。
难点:
- 正交多项式的具体形式和性质可能比较抽象和难以理解。
- 高斯型求积公式中的待定系数和节点需要通过解方程组来求解,这个过程可能需要一定的数值计算知识。
易错点:
- 选择适当的正交多项式和带权函数是构造高斯型求积公式的关键,不同的问题需要选择不同的正交多项式和带权函数。
- 求解待定系数和节点时可能会出现误差积累和舍入误差等问题,需要注意数值计算精度的问题。
- 在使用高斯型求积公式进行数值积分时,需要注意所选用的节点数是否足够,以及权函数是否满足一定的条件,如连续或可微等。






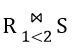




![[读书笔记] Variational AutoEncoders](https://img-blog.csdnimg.cn/d3b04b160a284d4abbe1bb48290e96b2.png#pic_center)