一、
我们先看下面这个算法当比较到不匹配的时候

模式串后移一位,并且让比较指针回去,这就叫做指针的回溯,回溯就是造成这个简单算法效率比较低的原因

这种是朴素模式匹配算法,时间复杂度比较高
int index(Str str,Str substr)
{
int i=1,j=1,k=1;//串从数组下标为1的位置开始存储,因此初值为1
while(i<i<=str.length && j<=substr.length)
{
if(str.ch[i]=substr.ch[j])
{
++i;
++j;
}
else
{
j=1;
i=++k;//匹配失败,i从主串的下一个位置开始,k中记录了上一次的起始位置
}
}
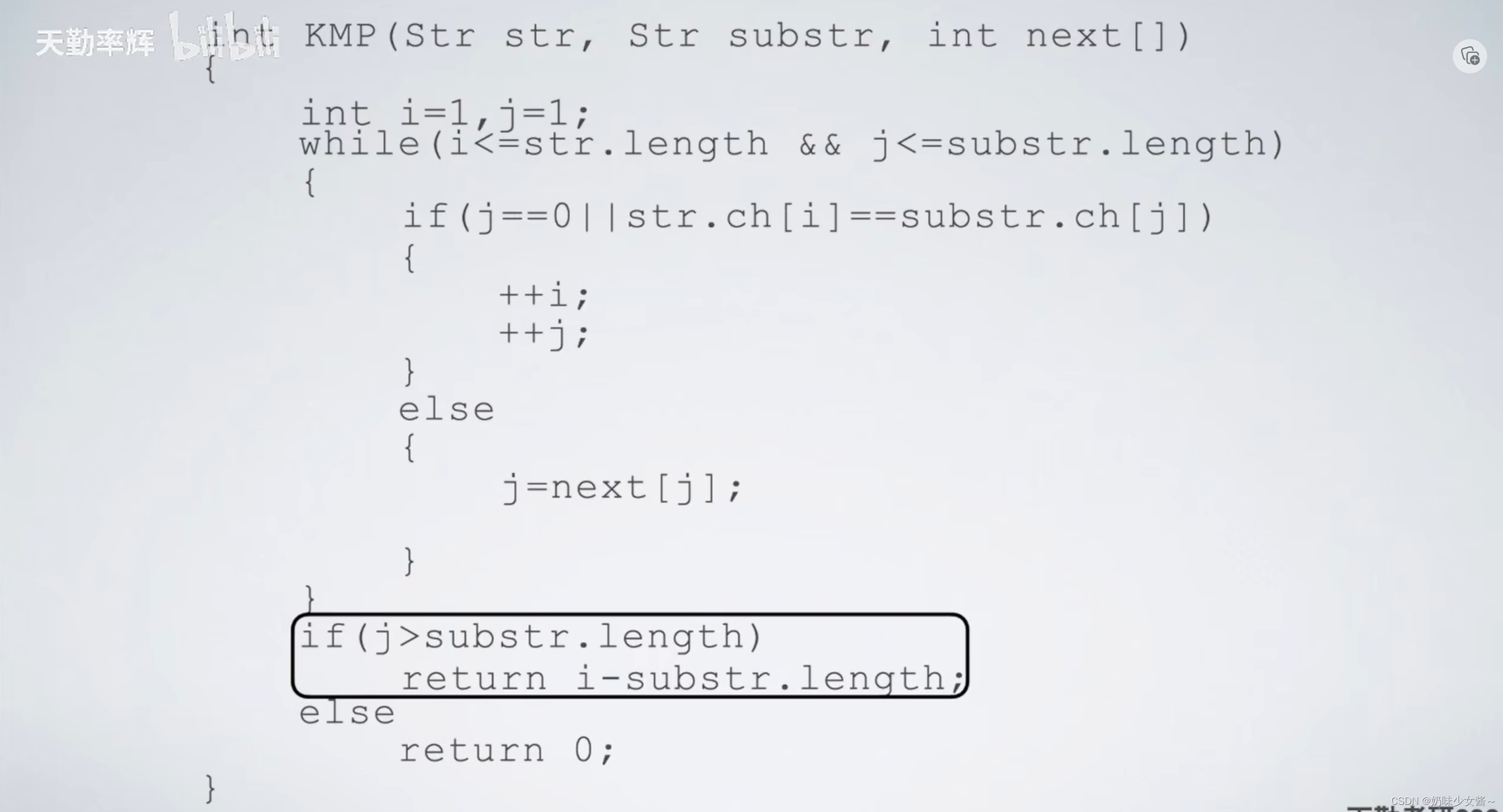
if(j>substr.length)
{
return k;
}
else
{
return 0;
}
}
下面是一个简单的例子:
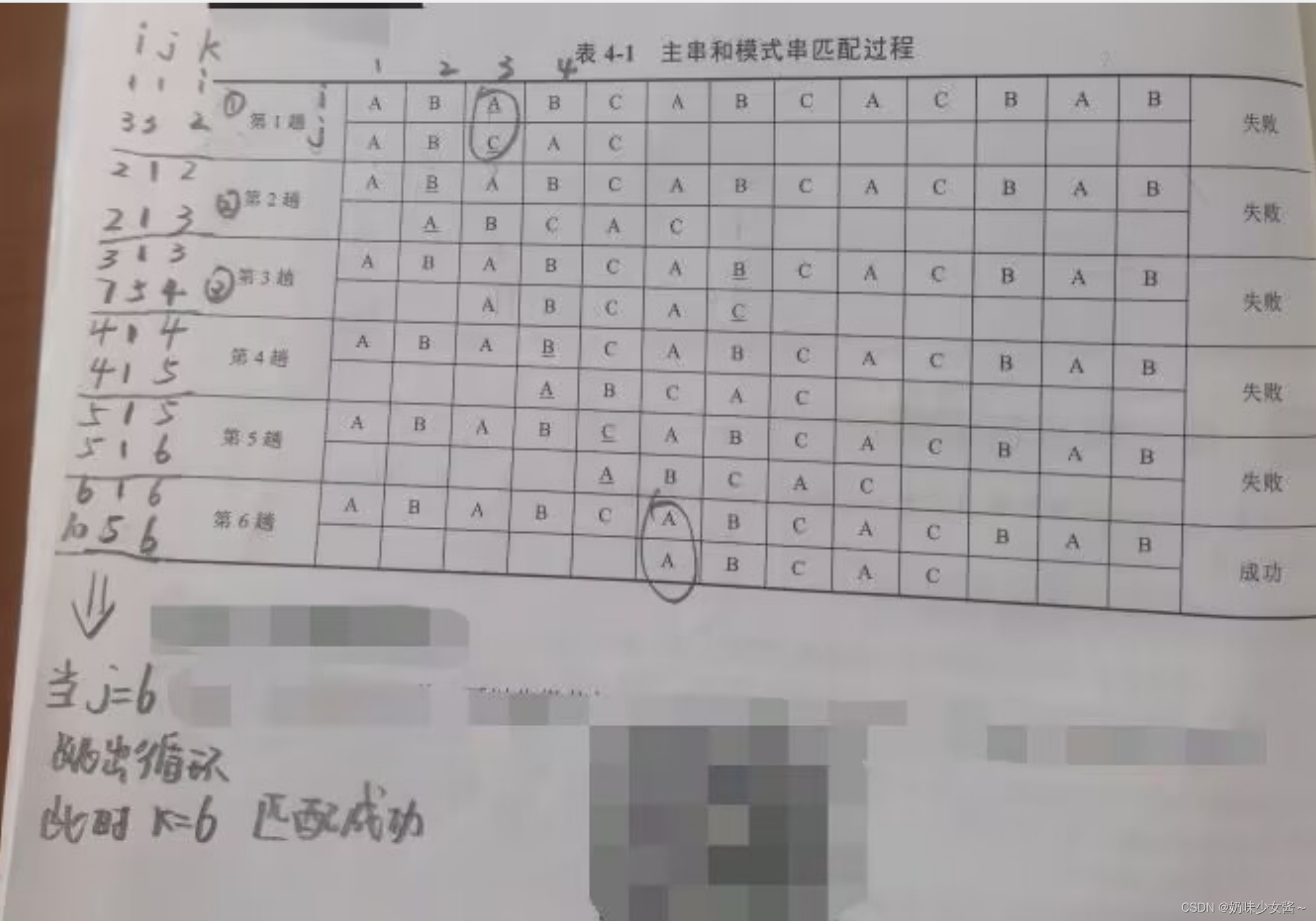
KMP算法就是从主串中找到与之相匹配的字串,KMP算法讲究的是一个快
我们回到刚刚位置不匹配的位置
第一比较指针左边上下两个字串是匹配的

而且这个模式串中有公共前后缀

接下来是KMP算法的核心要点,使得公共前后缀里的前缀移动到了原来后缀的位置
这样移动可以保证当前比较指针所在的位置左边的串上下是匹配的

当比较X的时候与主串不匹配的时候,只需要找出X之前的公共前后缀然后执行上述操作
如果模式串中有多个公共前后缀,那么我们就要取最长的那一个

接着我们继续移动

发现此时的移动后的模式串超出了主串的范围,所以就意味着匹配失败

再看一个例子



移动后就发现了匹配的情况

二、
假如第一个位置发生了不匹配的情况,让数组下标为1的字符与主串中的下一位进行比较



假如第二个位置发生了不匹配的情况,发现箭头左边的字串长度只有一,而我们要求的是公共前缀的长度要小于这个字串的长度,此时的公共前后缀的长度就为0了

指针左边的长度就是公共前后缀的长度,为0



这里的数组下标相当于公共前后缀的长度+1
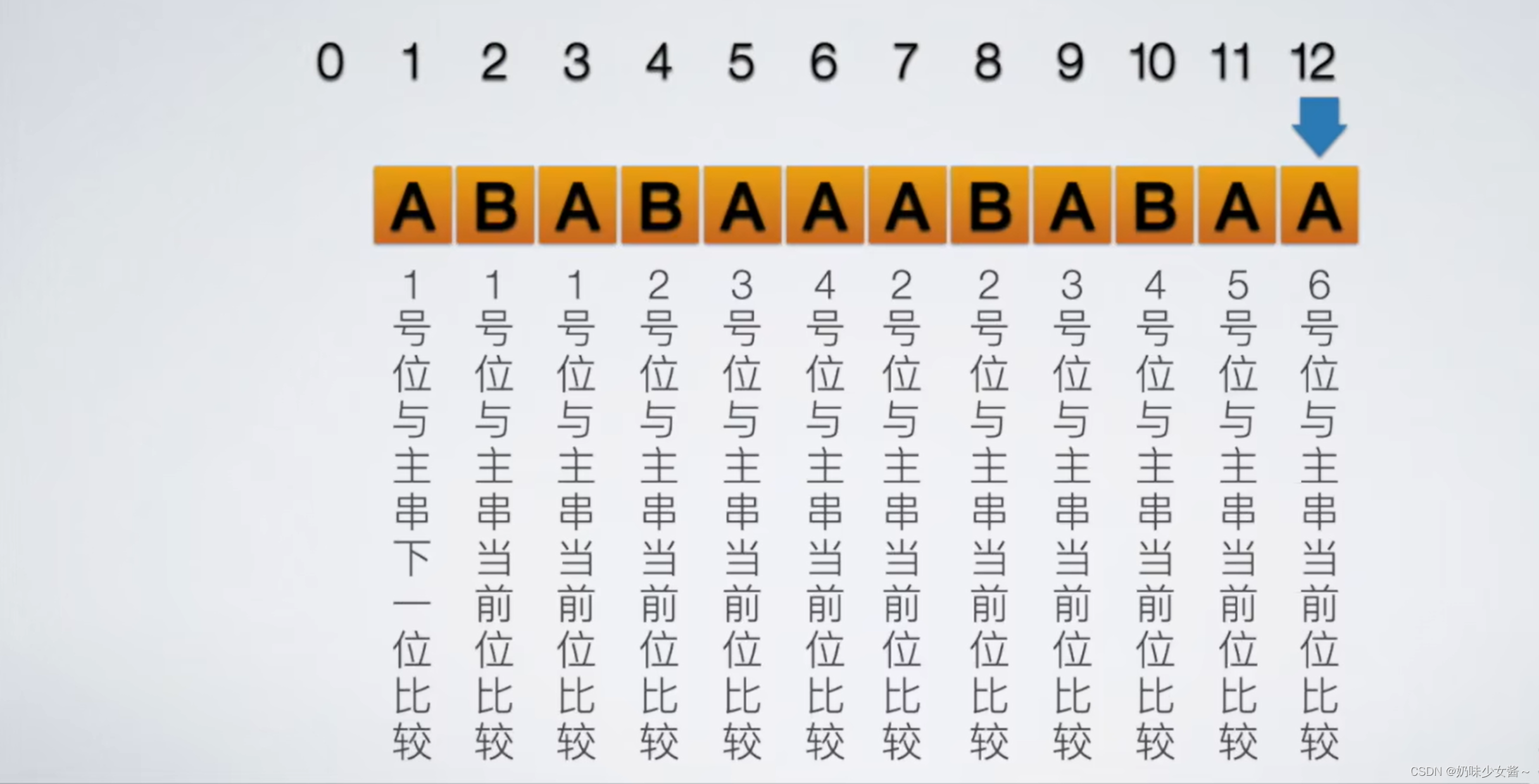


然后就要引出一个next数组
假设求串′ababaaababaa′的next数组
1、
2、前两个规定为0、1,上面述说了
3、比较第三位的时候他们的公共前后缀为0
next数组下标为1

4、比较第四位的时候,他们的公共前后缀为1 即a

next数组下标为2

5、比较第五位的时候,他们的公共前后缀为3 即ab

next数组下标为3

6、比较第六位的时候,他们的公共前后缀为aba


依次类推,不再赘述
三、求解next数组

上面的模式串红色部分为公共后缀
下面的模式串红色部分为公共前缀
长度为t-1
当前指针指向的那个是t
那么下一步就可以比较t+1的那个位置
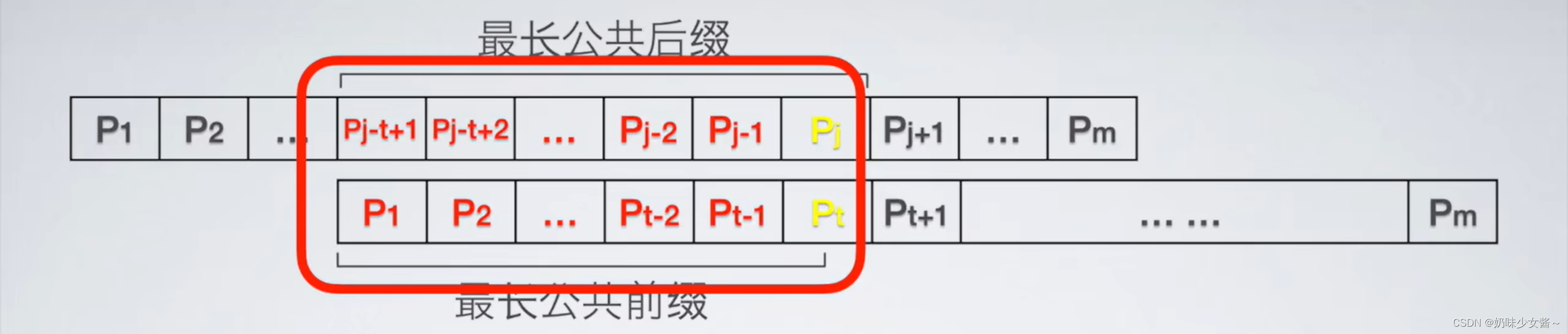
如果Pj=Pt的时候
两个相加之后会使得他们的公共前后缀加1
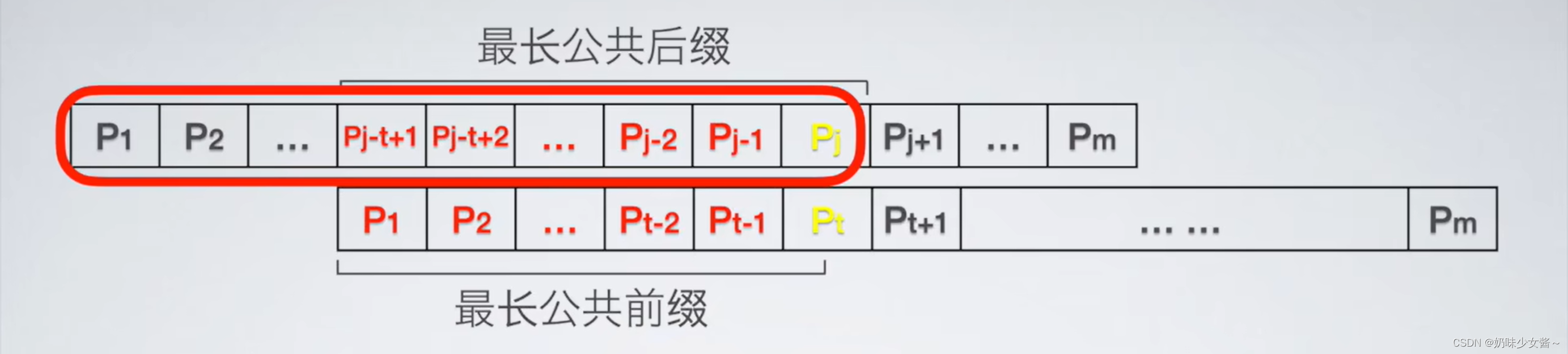
也就是这一段的公共前后缀